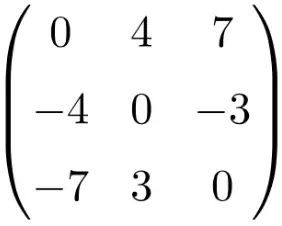Op deze pagina leggen we uit wat een vierkante matrix is en vind je voorbeelden van vierkante matrices. Daarnaast zie je welke eigenschappen vierkante matrices hebben, welke bewerkingen er mee gedaan kunnen worden en welke verschillende typen er bestaan.
Wat is een vierkante matrix?
Een vierkante matrix is a matrix die hetzelfde aantal rijen als kolommen heeft.
Voorbeelden van vierkante matrices
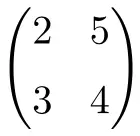
vierkante matrix van orde 2
vierkante matrix van orde 3
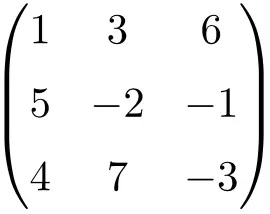
vierkante matrix van orde 4
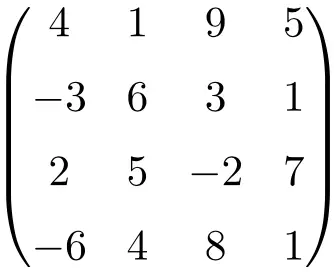
Zoals je kunt zien, worden vierkante matrices gewoonlijk genoemd in hun volgorde, dat wil zeggen dat een vierkante matrix van orde 2 betekent dat het een matrix is van dimensie 2×2 (2 rijen en 2 kolommen), of we spreken van een vierkante matrix van orde 3. wat aangeeft dat het de grootte 3×3 heeft (3 rijen en 3 kolommen).
Diagonalen van een vierkante matrix
De diagonalen van vierkante matrices hebben bepaalde namen, er is de hoofddiagonaal en de secundaire diagonaal:
- De hoofddiagonaal van een vierkante matrix bestaat uit de elementen die van de linkerbovenhoek naar de rechteronderhoek gaan:

- De secundaire diagonaal van een vierkante matrix komt overeen met de elementen die van de linker benedenhoek naar de rechter bovenhoek gaan:

Eigenschappen van een vierkante matrix
Vierkante matrices worden veel gebruikt in de lineaire algebra en daarom zijn ze zo belangrijk. Laten we dus eens kijken wat de kenmerken zijn die deze klasse matrices zo relevant maken:
- Elke vierkante matrix kan worden ontleed in een som van een symmetrische matrix en een antisymmetrische matrix .
- Als twee vierkante matrices van dezelfde orde zijn, kunnen ze van elkaar worden opgeteld of afgetrokken :
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- Twee vierkante matrices kunnen in beide mogelijke richtingen worden vermenigvuldigd . Het product van vierkante matrices is echter niet commutatief, dat wil zeggen dat het resultaat van de vermenigvuldiging zal veranderen afhankelijk van met welke kant het wordt vermenigvuldigd. Merk in het volgende voorbeeld op hoe het resultaat afhangt van de posities van de matrices:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Vierkante matrices zijn de enige die de determinant kunnen berekenen. Daarom kan een determinant alleen worden opgelost als deze een vierkante matrix is. Om bijvoorbeeld de determinant van een vierkante matrix van 3×3 te vinden, moet je de regel van Sarrus toepassen:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Bedenk ook dat als de determinant van de matrix anders is dan 0, dit betekent dat het een reguliere matrix is, dat wil zeggen dat hij omkeerbaar is. Aan de andere kant, als de determinant nul is, is het een singuliere matrix (die geen inverse heeft).
- Ten slotte kunnen vierkante matrices worden gediagonaliseerd . Zo kan een basisverandering worden uitgevoerd om de eigenwaarden (of eigenwaarden) en de eigenvectoren (of eigenvectoren) van een vierkante matrix te berekenen.
Bewerkingen met vierkante matrices
Zoals we hebben gezien kan de determinant van een matrix alleen worden berekend als de matrix vierkant is. Op dezelfde manier zijn er ook bepaalde bewerkingen die alleen kunnen worden uitgevoerd als de matrix een vierkante afmeting heeft:
spoor van een matrix
Het spoor van een matrix is de som van de elementen die de hoofddiagonaal van een vierkante matrix vormen.
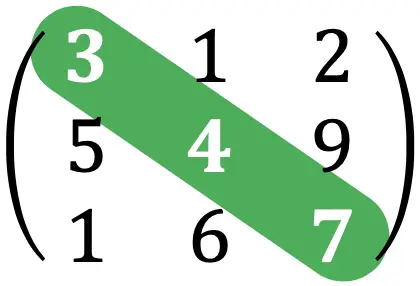
Het spoor van de matrix uit de bovenstaande oefening zou er bijvoorbeeld als volgt uitzien:
![]()
Soorten vierkante matrijzen
Dan heb je de belangrijkste soorten vierkante matrices die er bestaan. Klik op het type dobbelsteen en ontdek wat er speciaal aan is.
Zoals je kunt zien, zijn er veel soorten vierkante matrices, en elk heeft om een andere reden zijn eigen naam.