Hier vindt u hoe de ellipsvergelijking (formule) wordt berekend, ongeacht of deze de oorsprong als middelpunt heeft of niet. Ook vindt u wat de elementen van de ellips zijn, hoe u ze berekent en waarvoor ze worden gebruikt. Bovendien kunt u voorbeelden en opgeloste oefeningen van ellipsvergelijkingen zien.
Formule voor ellipsvergelijking
De formule voor de vergelijking van de ellips in cartesiaanse coördinaten is:
![]()
Goud:
-

En

zijn de coördinaten van het midden van de ellips:
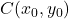
-

is de horizontale straal van de ellips.
-

is de verticale straal van de ellips.
Vergelijking van de ellips gecentreerd op de oorsprong
Een veel voorkomend type ellips is een ellips waarvan het middelpunt zich in de oorsprong van de coördinaten bevindt, dat wil zeggen in het punt (0,0). Dit is de reden waarom we zullen zien hoe we de vergelijking van de ellips met het middelpunt in de oorsprong kunnen vinden.
Volg de formule voor de ellipsvergelijking:
![]()
Als de ellips gecentreerd is op de oorsprong van de coördinaten, betekent dit dat
![]()
En
![]()
zijn gelijk aan 0, dus je vergelijking wordt:
![]()
Er zijn wiskundigen die deze uitdrukking ook wel de canonieke vergelijking of de gereduceerde vergelijking van de ellips noemen.
elementen van de ellips
Zodra we zien hoe de vergelijking van de ellips eruit ziet, zullen we zien wat de elementen ervan zijn. Maar laten we eerst onthouden wat een ellips precies is:
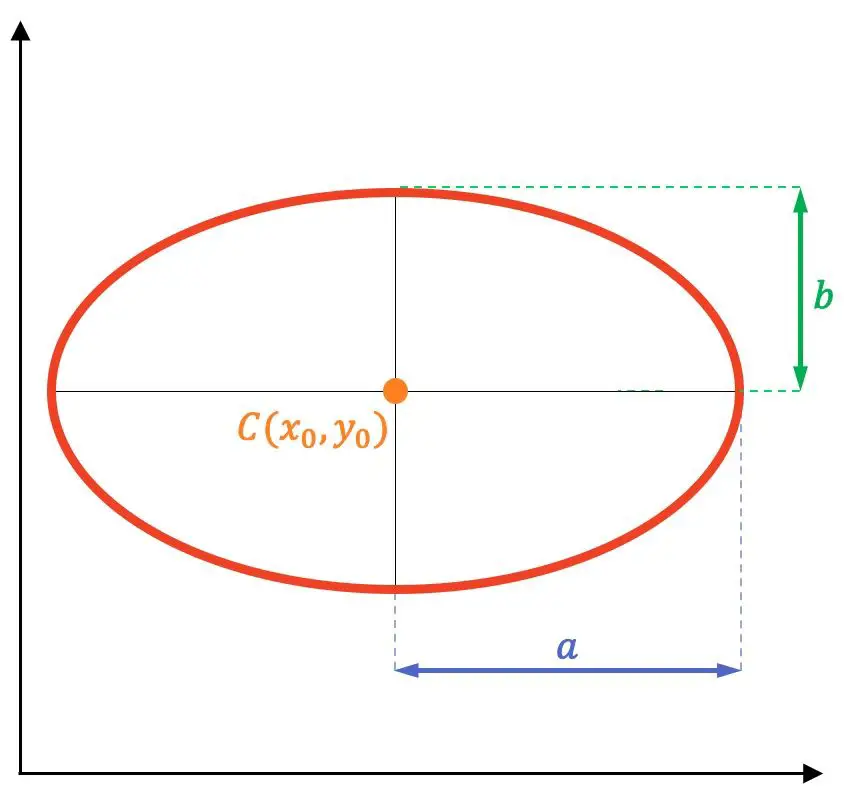
De ellips is een platte, gesloten, gebogen lijn die sterk lijkt op de omtrek, maar de vorm is meer ovaal. In het bijzonder is de ellips de meetkundige plaats van alle punten van een vlak waarvan de som van de afstanden tot twee andere vaste punten (de zogenaamde brandpunten F en F’) constant is.
De elementen van een ellips zijn dus:
- De brandpunten : dit zijn de vaste punten F en F’ (paars gekleurde punten in onderstaande afbeelding). De som van de afstanden tussen elk punt op de ellips en elk brandpunt is constant voor alle punten op de ellips.
- Hoofd- of brandpuntsas : dit is de symmetrieas van de ellips waarin het brandpunt zich bevindt. Ook wel hoofdas genoemd.
- Secundaire as : dit is de symmetrieas van de ellips loodrecht op de hoofdas. Het wordt ook wel de kleine as genoemd en komt overeen met de middelloodlijn van het segment dat de brandpunten verbindt.
- Midden : is het snijpunt van de assen van de ellips. Bovendien is dit het symmetriecentrum van de ellips (oranje stip in de grafiek).
- Hoekpunten : snijpunten van de ellips met zijn symmetrieassen (zwarte punten).
- Semi-hoofdas of hoofdas: segment dat loopt van het midden van de ellips naar de hoekpunten van de hoofdas.
- Semi-kleine as of secundaire as: segment tussen het midden van de ellips en de hoekpunten van de secundaire as.
- Brandpuntsafstand : Dit is de afstand tussen de twee brandpunten.
- Semi-brandpuntsafstand : komt overeen met de afstand tussen het centrum en elk van de brandpunten.
- De radiovectoren : zijn de segmenten die elk punt van de ellips met elk focus verbinden (blauwe segmenten in de grafiek).

Relatie tussen elementen van een ellips
De verschillende elementen van een ellips zijn met elkaar verbonden. Bovendien zijn de relaties daartussen erg belangrijk voor oefeningen op ellipsen, omdat ze meestal nodig zijn voor het oplossen van problemen op ellipsen en het bepalen van hun vergelijkingen.
Zoals we hierboven bij de definitie van de ellips hebben gezien, is de afstand van elk punt op de ellips tot het brandpunt F plus de afstand van hetzelfde punt tot het brandpunt F’ constant. Welnu, deze constante waarde is gelijk aan tweemaal wat de semi-hoofdas meet. Met andere woorden, de volgende gelijkheid geldt voor elk punt op een ellips:
![]()
Goud
![]()
En
![]()
is de afstand van punt P tot respectievelijk focus F en F’ en
![]()
is de lengte van de semi-focale as.
Omdat het hoekpunt van de secundaire as zich precies in het midden van de brandpuntsas bevindt, is de afstand daarvan tot een van de brandpunten daarom gelijk aan de lengte van de semi-primaire as (
![]()
):
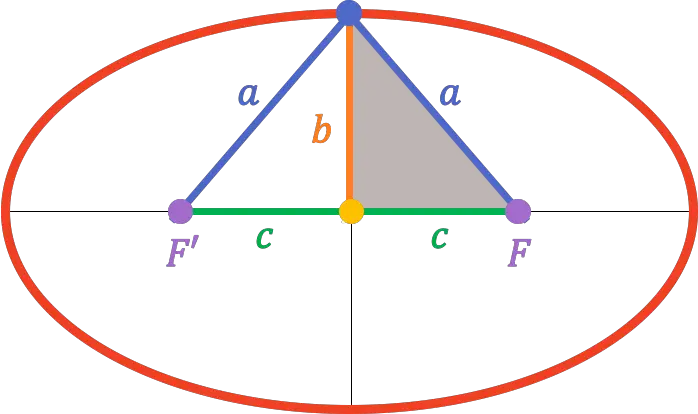
Uit de stelling van Pythagoras is het dus mogelijk om de relatie te vinden die bestaat tussen de hoofdhalve as, de secundaire halve as en de halve brandpuntsafstand:
![]()
Onthoud deze formule omdat deze erg handig zal zijn voor het berekenen van de resultaten van oefeningen met ellipsen.
Ellips-excentriciteit
Het is duidelijk dat niet alle ellipsen hetzelfde zijn, maar sommige zijn langwerpiger en andere zijn meer afgevlakt. Er is dus een coëfficiënt die wordt gebruikt om te meten hoe afgerond een bepaalde ellips is. Deze coëfficiënt wordt excentriciteit genoemd en wordt berekend met de volgende formule:
![]()
Goud
![]()
is de afstand van het midden van de ellips tot een van zijn brandpunten en
![]()
de lengte van de semi-hoofdas.
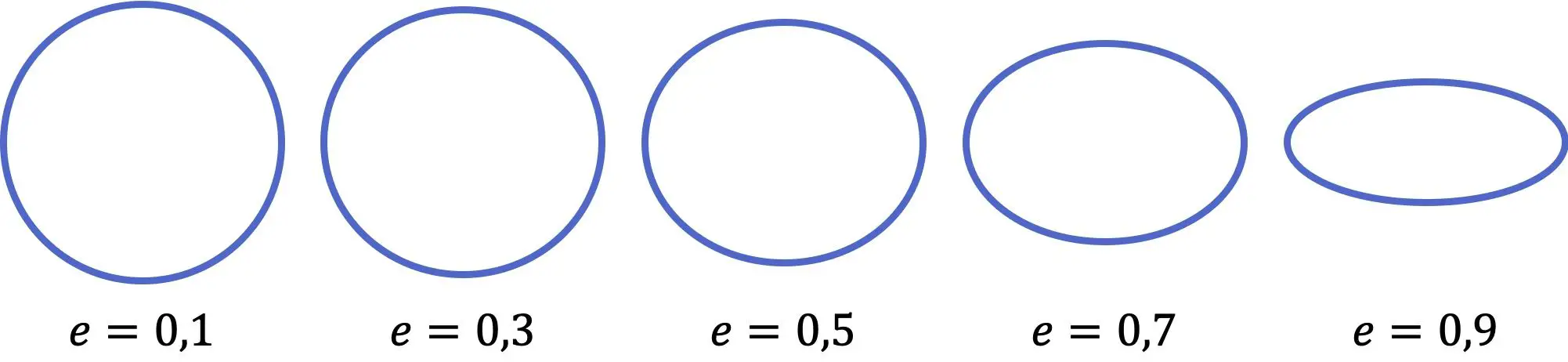
Zoals je in de vorige weergave kunt zien, geldt: hoe kleiner de waarde van de excentriciteit van de ellips, hoe meer deze op een cirkel lijkt. Aan de andere kant geldt: hoe groter de coëfficiënt, hoe platter de ellips. Bovendien varieert de excentriciteitswaarde van nul (perfecte cirkel) tot één (horizontale lijn), beide niet inclusief.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1 C(3,1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= een 4= een
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Ten slotte, als dit artikel nuttig voor u was, zult u zeker ook geïnteresseerd zijn in onze pagina’s over de hyperboolformule en de paraboolformule . Je vindt er een gedetailleerde uitleg over wat de hyperbool en de parabool zijn, hun vergelijkingen, hun kenmerken, voorbeelden, opgeloste oefeningen,…