Hier vindt u de uitleg van wat vergelijkbare monomials zijn. Daarnaast kun je voorbeelden van vergelijkbare monomials zien en zelfs oefenen met opgeloste oefeningen van dit soort monomials.
Wat zijn vergelijkbare monomialen?
Om de betekenis van soortgelijke monomialen te begrijpen, moet je uiteraard eerst weten wat een monomial is . Daarom raad ik u aan de gelinkte pagina te bekijken voordat u verdergaat.
Dus dat twee monomialen vergelijkbaar zijn, betekent het volgende:
Soortgelijke monomials zijn monomials die precies hetzelfde letterlijke deel hebben. Met andere woorden, twee of meer monomialen zijn vergelijkbaar als ze zijn samengesteld uit dezelfde variabelen (letters) en dezelfde exponenten.
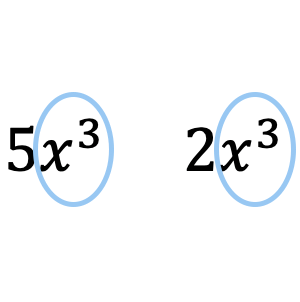
Zoals je in het bovenstaande voorbeeld kunt zien, de monomial
![]()
is vergelijkbaar met de monomial
![]()
omdat ze allebei hetzelfde letterlijke deel hebben
![]()
zelfs als hun coëfficiënten verschillend zijn.
Een van de kenmerken van vergelijkbare monomials is dat ze worden gebruikt voor zowel het optellen van monomials als het aftrekken van monomials , twee bewerkingen die je ja of ja moet beheersen. Klik op een van de twee links om te zien hoe u monomials kunt optellen of aftrekken. Bovendien vindt u in elke link voorbeelden en oefeningen die stap voor stap worden opgelost.
In feite kun je monomialen alleen optellen en aftrekken als ze vergelijkbaar zijn. En dit is precies waarom vergelijkbare monomieën zo belangrijk zijn in de wiskunde.
Voorbeelden van soortgelijke monomialen
Zodat u het concept van soortgelijke monomialen volledig kunt begrijpen, ziet u hieronder verschillende voorbeelden van monomialen die op elkaar lijken.
voorbeeld 1
![]()
De twee voorgaande monomialen zijn vergelijkbaar omdat hun letterlijke delen gelijkwaardig zijn
![]()
Voorbeeld 2
![]()
De voorgaande drie monomials zijn vergelijkbaar omdat hun letterlijke delen hetzelfde zijn
![]()
Voorbeeld 3
![]()
![]()
De voorgaande vier monomials lijken op elkaar omdat hun letterlijke delen identiek zijn
![]()
Opgeloste oefening van soortgelijke monomials
Match paren van monomials die op elkaar lijken:
![Rendered by QuickLaTeX.com \begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ca52625823eec990ff41ecd05d5c1149_l3.png)
Soortgelijke monomials zijn monomials die dezelfde letterlijke delen hebben. Daarom zijn paren van vergelijkbare monomialen:
![]()
![]()
![]()
![]()
Hoewel het iets heel anders betekent, ben je, als je zover bent gekomen, waarschijnlijk ook geïnteresseerd in wat de polynomiale ontbinding van een getal is. Omdat dit iets is waar heel weinig mensen vanaf weten, maar het is eigenlijk heel nuttig om wiskundige uitdrukkingen te vereenvoudigen.