Vectoraftrekking

Op deze pagina ziet u hoe u twee vectoren kunt aftrekken, zowel grafisch als numeriek. Om ze grafisch af te trekken zijn er drie methoden: het parallellogram, de driehoek en de veelhoek. Hier kunt u de voor- en nadelen van elke methode onderscheiden. Daarnaast vind je voorbeelden, oefeningen en problemen die stap voor stap worden opgelost.

Hoe kan ik twee vectoren grafisch aftrekken?

Er zijn verschillende manieren om vectoren geometrisch af te trekken. Uiteraard wordt met alle methoden hetzelfde resultaat verkregen, maar we zullen u alle methoden uitleggen, zodat u degene kunt kiezen die u verkiest. 👌

Om slechts 2 vectoren af te trekken, zijn er twee grafische procedures: de parallellogrammethode en de driehoeksmethode . Als we echter het aftrekken van 3 of meer vectoren willen oplossen, moeten we de polygoonmethode gebruiken.

Dus, en zonder verder oponthoud, vindt u hieronder de uitleg van al deze methoden.

Parallellogrammethode of regel

De parallellogramregel of parallellogrammethode is een procedure waarmee u op een zeer eenvoudige manier de aftrekking van twee vectoren kunt vinden via de grafische weergave. De stappen die u moet volgen om dit proces toe te passen, zijn als volgt:

1. Eerst vertegenwoordigen we de twee vectoren in de grafiek en plaatsen ze op hetzelfde toepassingspunt, dat wil zeggen dat we de oorsprong van beide vectoren op hetzelfde punt plaatsen.
2. Ten tweede tekenen we de tegenovergestelde vector van de vector die wordt afgetrokken in de bewerking, of met andere woorden: we keren de vector om die wordt afgetrokken.
3. Vervolgens trekken we een lijn evenwijdig aan de vector met tekenverandering aan het einde van de vector die wordt toegevoegd. En we herhalen het proces met de andere vector. Zodat we de tekening van een parallellogram krijgen (vandaar de naam van de regel).
4. Ten slotte zal het resultaat van de aftrekking de vector zijn die loopt van de gemeenschappelijke oorsprong van de twee vectoren naar het punt waar de twee parallelle lijnen elkaar snijden.

Beschouw het volgende algemene voorbeeld waarin twee vectoren worden afgetrokken met behulp van de parallellogrammethode:

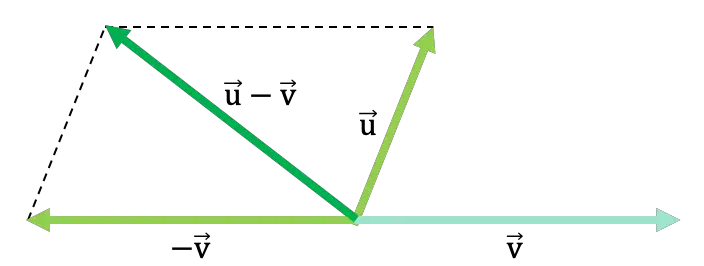
Driehoeksmethode of regel

De driehoeksmethode is een andere procedure waarmee twee vectoren van hun grafiek kunnen worden afgetrokken. In dit geval zijn de te volgen stappen:

1. Plaats de twee vectoren op hetzelfde toepassingspunt, dat wil zeggen zo dat de twee vectoren hetzelfde punt hebben als hun oorsprong.
2. Het resultaat van vectoraftrekking is het segment dat van het einde van de aftrekkende vector naar het einde van de andere vector gaat. Als je goed kijkt, wordt een driehoek voltooid waarbij de twee vectoren worden afgetrokken en de vector wordt afgetrokken.

Hier is een voorbeeld van vectoraftrekken met behulp van de driehoeksmethode:

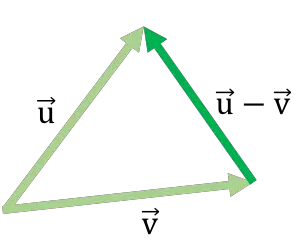
Deze manier om vectoren af te trekken is vergelijkbaar met de kop-staartmethode die wordt gebruikt om vectoren op te tellen .

veelhoek methode

Als we eenmaal hebben gezien hoe we het aftrekken van twee vectoren grafisch kunnen oplossen, zullen we zien hoe het moet als we meer dan twee vectoren hebben.

Als je drie of meer vectoren wilt aftrekken, is er een techniek om sneller te gaan in de berekening en alle vectoren in één keer af te trekken. Deze techniek wordt de polygoonmethode genoemd en bestaat uit het achtereenvolgens toepassen van de kop-staartmethode van vectoroptelling.

Nu denk je waarschijnlijk: vectoren toevoegen ? Het is verkeerd gecorrigeerd… Nou nee! eh eh

Het blijkt dat het aftrekken van twee vectoren hetzelfde is als het optellen van een vector plus de tegenovergestelde (of negatieve) vector van de aftrekkende vector. Dit komt door de optellings- en aftrekkingseigenschappen van vectoren:

Daarom zijn de stappen die we moeten volgen om 3 of meer vectoren af te trekken met de polygoonmethode:

1. Eerst moeten we de inverse vector van elke aftrekvector vinden. Het is zo simpel als het omkeren van de richting en richting van alle vectoren die worden afgetrokken.
2. Vervolgens plaatsen we elke tegengestelde vector naast de vector die u niet aftrekt, de een na de ander. Zodat de oorsprong van een vector samenvalt met het einde van een andere vector.
3. Ten slotte is het resultaat van vectoraftrekking de vector die wordt verkregen door het begin van de eerste vector te verbinden met het einde van de laatste vector.

Kijk naar het volgende voorbeeld waarin een aftrekking wordt gedaan met 4 vectoren:

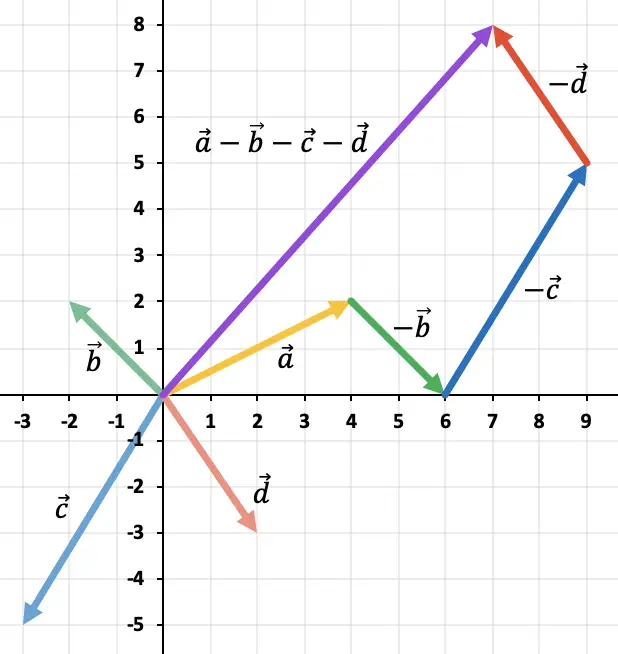
Merk op dat om de tegengestelde vector van een vector te vinden, de twee componenten van de vector van teken moeten veranderen.

Hoe bereken je numeriek het aftrekken van twee vectoren?

Zodra we al weten hoe we vectoren van de grafiek moeten aftrekken, zullen we zien hoe we een vectoraftrekking numeriek of algebraïsch kunnen berekenen.

Bijvoorbeeld aftrekken tussen vectoren

En

Oosten:

Opgeloste vectoraftrekkingsproblemen

Oefening 1

Bereken vectoraftrekking grafisch

minder

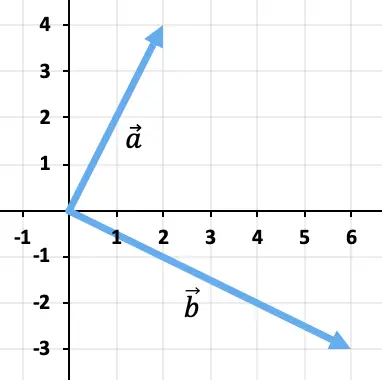
Om de twee vectoren van elkaar af te trekken, gebruiken we de driehoeksmethode. De punten zijn al op hetzelfde toepassingspunt geplaatst (de oorsprong van de coördinaten), dus het resultaat van het aftrekken zal de vector zijn die loopt vanaf het einde van

aan het einde van

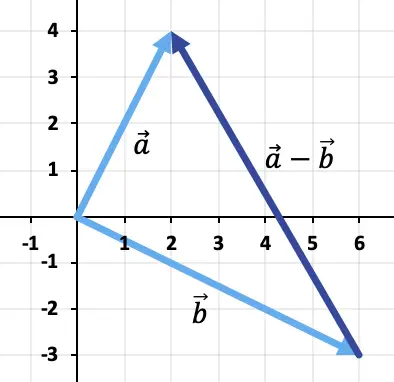
Oefening 2

Vind het aftrekken van vectoren grafisch

minder

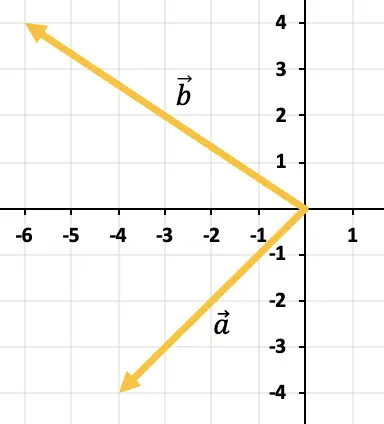
Om de twee vectoren van elkaar af te trekken, gebruiken we de driehoeksregel. De punten zijn al op hetzelfde toepassingspunt geplaatst (aan het begin van de X-as en de Y-as), dus het resultaat van het aftrekken zal de vector zijn die loopt vanaf het einde van

aan het einde van

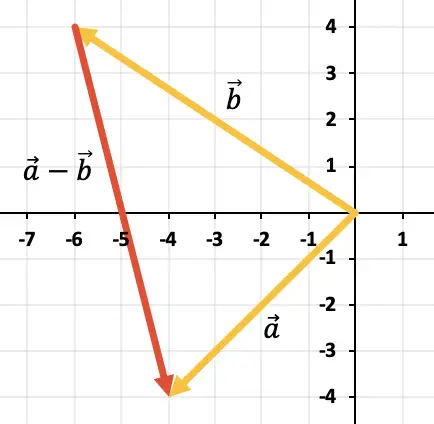
Oefening 3

Los de volgende vectorbewerking grafisch op:

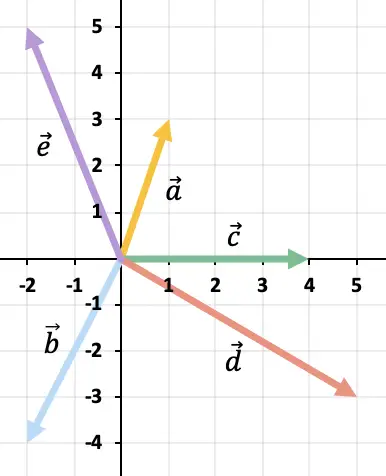
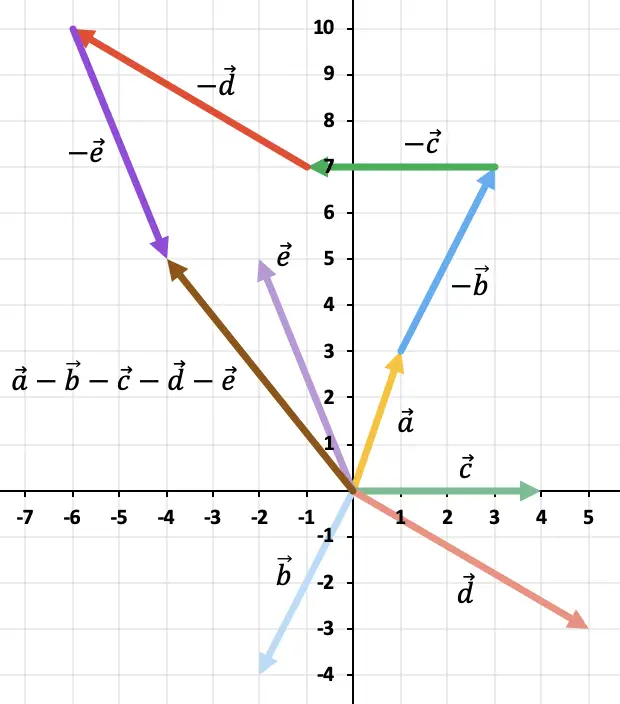
Omdat er meer dan twee vectoren zijn, zullen we de polygoonregel gebruiken om de vectoraftrekking op te lossen. Om dit te doen, moeten we de tegengestelde vectoren van de resterende vectoren na elkaar weergeven. En het resultaat zal de vector zijn die begint bij de oorsprong van de vector

tot waar de laatste tegengestelde vector eindigt.

Oefening 4

Bepaal numeriek het resultaat van het aftrekken van de volgende vectoren:

Om twee vectoren numeriek af te trekken, moet u hun respectievelijke coördinaten aftrekken:

Oefening 5

Los analytisch de volgende vectorbewerking op:

Om vectoren numeriek (of analytisch) af te trekken, moeten we hun respectieve componenten aftrekken: