Stelsels van vergelijkingen zijn sets van twee of meer vergelijkingen met meer dan één onbekende. Om systemen op te lossen kunnen we dus vier methoden gebruiken: substitutie, egalisatie, reductie en grafieken. Maar voordat we beginnen met het uitleggen van de oplossingsprocedures, zullen we de soorten systemen definiëren die bestaan op basis van het aantal oplossingen:
- Bepaald compatibel systeem: het heeft slechts één oplossing en kan worden weergegeven door twee lijnen die elkaar in één punt snijden (wat de oplossing is).
- Onbepaald compatibel systeem: het heeft oneindige oplossingen en dit komt door het feit dat er twee lijnen zijn die op dezelfde punten samenvallen.
- Incompatibel systeem: het heeft geen oplossing, aangezien de lijnen evenwijdig zijn en daarom geen gemeenschappelijk punt hebben.
Methoden voor het oplossen van stelsels van lineaire vergelijkingen
We zullen nu de verschillende systemen uitleggen die we kunnen gebruiken om stelsels vergelijkingen op te lossen. In de uitleg vind je de theorie en enkele voorbeelden, waardoor alle uitgelegde concepten duidelijker zullen zijn. Merk op dat we in dit artikel alleen zullen praten over systemen van 2×2 vergelijkingen , wat betekent dat we eenvoudigweg te maken zullen hebben met systemen die uit twee vergelijkingen bestaan. Dat gezegd hebbende, laten we beginnen met de uitleg.
vervangingsmethode
De substitutiemethode bestaat uit het isoleren van een van de onbekenden in een van de vergelijkingen en het vervolgens vervangen van de verkregen uitdrukking in de tegenovergestelde vergelijking. Deze methode wordt het meest aanbevolen als ten minste één van de onbekenden de waarde van de coëfficiënt gelijk heeft aan 1. De te volgen stappen zijn dus heel eenvoudig:
- Isoleer een onbekende grootheid uit een van de twee vergelijkingen.
- Vervang in de andere vergelijking de uitdrukking die equivalent is aan het onbekende die we uit de eerste vergelijking hebben geëlimineerd.
- Wis de tegenovergestelde onbekende in de vergelijking die we hebben verkregen.
- Zodra we de waarde van de eerste variabele hebben, moeten we deze gebruiken om de tweede te vinden.
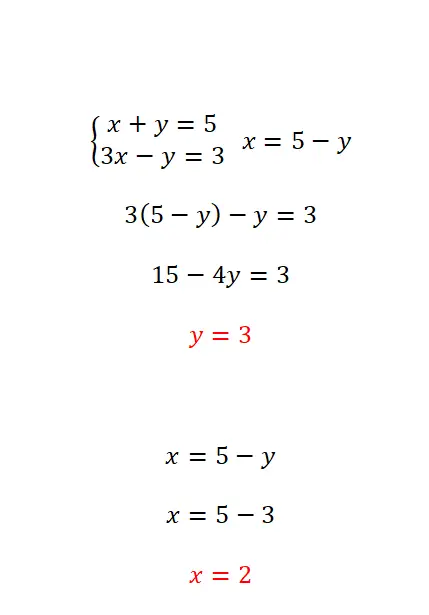
egalisatie methode
De matchingmethode bestaat uit het isoleren van dezelfde variabele in de twee vergelijkingen en het matchen van de twee verkregen uitdrukkingen. Deze methode wordt aanbevolen als dezelfde onbekende gemakkelijk in beide vergelijkingen kan worden geïsoleerd, omdat de hele berekening hierdoor eenvoudiger wordt. De procedure die u in dit geval moet volgen is als volgt:
- We isoleren het onbekende dat we hebben gekozen in de twee vergelijkingen.
- We assimileren de equivalente uitdrukkingen voor dit onbekende.
- We lossen de vergelijking normaal op.
- De andere onbekende berekenen we met de door ons berekende waarde.
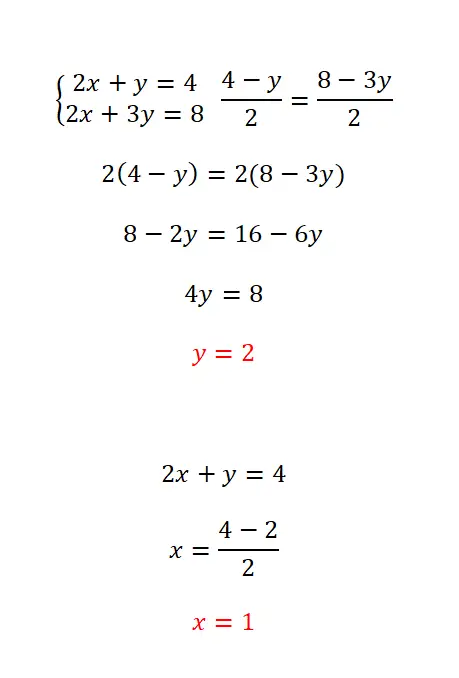
reductie methode
De reductiemethode is gebaseerd op het vermenigvuldigen van beide vergelijkingen met twee getallen, waardoor we dezelfde coëfficiënt kunnen verkrijgen met een ander teken van een van de variabelen in beide uitdrukkingen. Deze methode wordt het meest aanbevolen als dezelfde onbekende dezelfde coëfficiënt heeft in alle vergelijkingen of als er dezelfde coëfficiënten van tegengestelde tekens zijn. En de oplossingsprocedure is als volgt:
- De twee vergelijkingen worden vermenigvuldigd met de benodigde getallen (je moet twee getallen vinden die het mogelijk maken dezelfde coëfficiënt te verkrijgen voor een van de twee variabelen in de twee vergelijkingen, maar met tegengesteld teken).
- Vervolgens worden de vergelijkingen afgetrokken of opgeteld om dit onbekende met hun respectieve coëfficiënten te elimineren.
- Vervolgens wordt de resterende vergelijking opgelost.
- En we gebruiken het resultaat van deze vergelijking om de numerieke waarde te krijgen die we missen in de andere variabele.
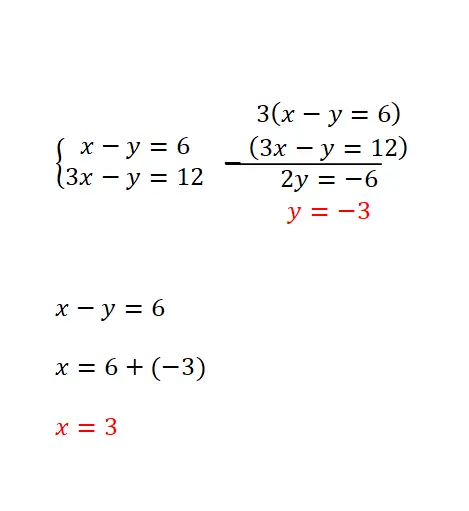
grafische methode
Ten slotte kunnen we ervoor kiezen om een stelsel vergelijkingen op te lossen door middel van een grafische weergave . Deze methode verschilt nogal van de andere, omdat ze geen complex wiskundig gedeelte heeft, maar bijna volledig grafisch is. Om de waarden van de onbekenden te kennen, moeten we dus de twee vergelijkingen structureren in de vorm van de vergelijking van de lijn: y = mx + b . Op deze manier kunnen we de representatie maken, we zullen de waarden van de coördinaten van het snijpunt tussen de twee functies associëren met de onbekenden. Hier is een uitgewerkt voorbeeld:
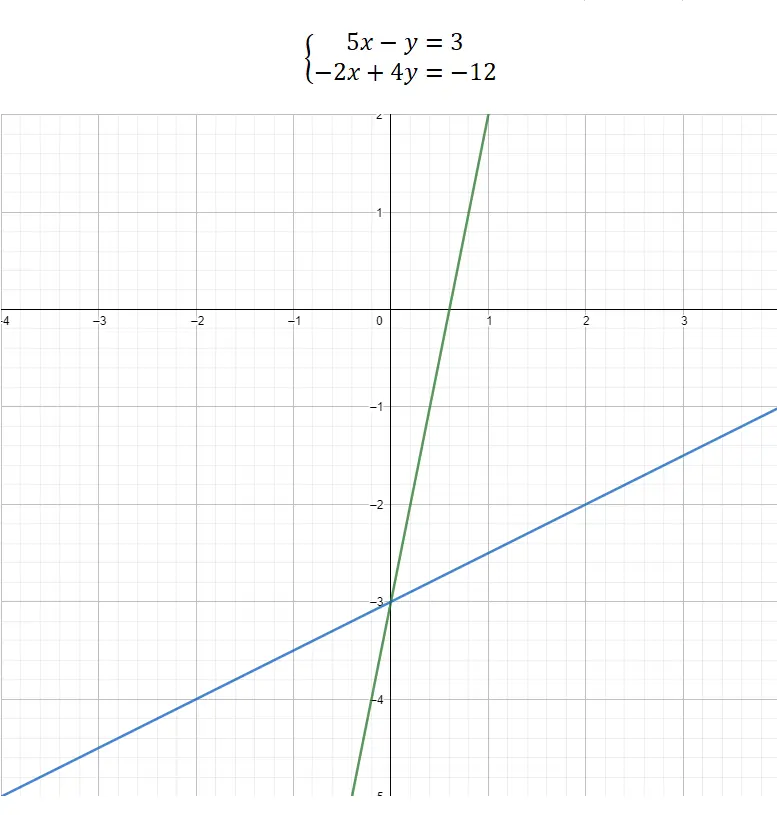
Zoals u in de grafiek kunt zien, is het grenspunt tussen de twee functies (0, -3). Daarom is de waarde van x = 0 en de waarde van y = -3. Dit is hoe een stelsel vergelijkingen grafisch wordt opgelost.
Hoe los je een stelsel kwadratische vergelijkingen op?
Om stelsels kwadratische vergelijkingen op te lossen, kunnen we de methoden gebruiken die we zojuist hebben besproken. Persoonlijk raden wij graag de substitutiemethode aan, omdat we hierdoor snel een vergelijking kunnen krijgen met één enkele onbekende. Aan de andere kant, als we de reductie- of egalisatiemethoden gebruiken, wordt de berekening behoorlijk ingewikkeld. Dus zodra u een van de twee variabelen heeft vervangen, hoeft u alleen de resulterende kwadratische vergelijking of kwadratische vergelijking op te lossen. Hier is een voorbeeld zodat u het hele proces kunt zien:
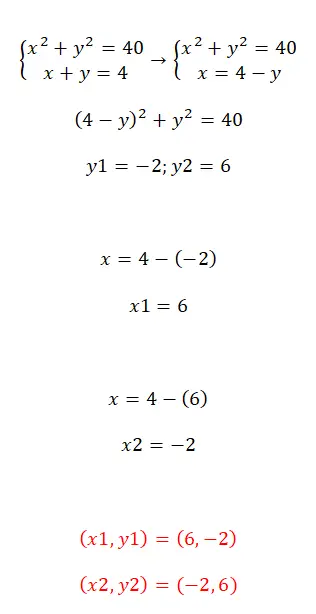
Oefeningen over het oplossen van stelsels vergelijkingen
We bieden je nu enkele oefeningen aan over stelsels van lineaire en kwadratische vergelijkingen, zodat je de uitgelegde theorie kunt toepassen. Op deze manier zul je alle concepten die verband houden met het berekenen van stelsels van vergelijkingen beter begrijpen. We raden u aan deze eerst op te lossen voordat u naar de antwoorden kijkt die wij bieden. Op deze manier haalt u het meeste uit de oefeningen:
Oefening 1
Los dit stelsel vergelijkingen op met behulp van de substitutiemethode:
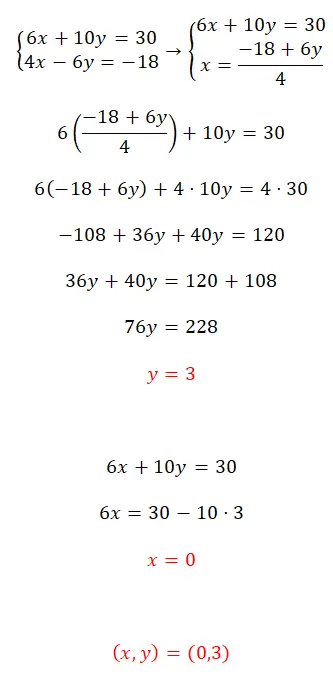
- We beginnen met het isoleren van een van de twee onbekenden in een vergelijking.
- Vervolgens vervangen we de uitdrukking verkregen in de tegenovergestelde vergelijking door het onbekende dat we eerder hebben opgelost.
- We verkrijgen dan het resultaat van de tegenovergestelde variabele.
- Vervolgens vervangen we de eerste ontdekte waarde in een van de twee vergelijkingen om de waarde van de eerste onbekende te berekenen.
- Ten slotte drukken we het resultaat van de twee variabelen uit.
Oefening 2
Los dit stelsel vergelijkingen op met behulp van de substitutiemethode:
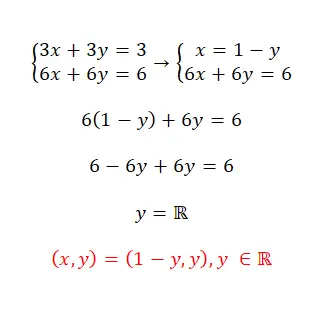
- In dit geval volgen we dezelfde procedure: isoleren een onbekende, vervangen deze in de andere uitdrukking en isoleren de tweede variabele.
- Zoals we kunnen zien, is dit een onbepaald compatibel systeem, omdat het oneindig veel oplossingen heeft.
Oefening 3
Los dit stelsel vergelijkingen op met behulp van de egalisatiemethode:
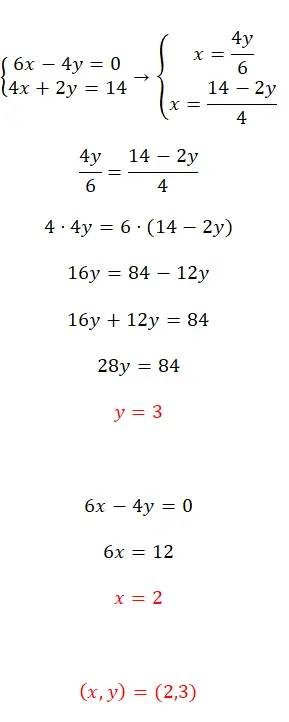
- De eerste stap is het isoleren van dezelfde variabele in beide vergelijkingen, in dit geval hebben we x gekozen.
- Vervolgens matchen we de resulterende uitdrukkingen en beginnen we met oplossen.
- Zo verkrijgen we de waarde van de eerste onbekende.
- En als we dit in een van de twee oorspronkelijke vergelijkingen vervangen, kunnen we de tweede onbekende berekenen.
- Ten slotte drukken we het resultaat van de twee variabelen uit.
Oefening 4
Los dit stelsel vergelijkingen op met behulp van de egalisatiemethode:
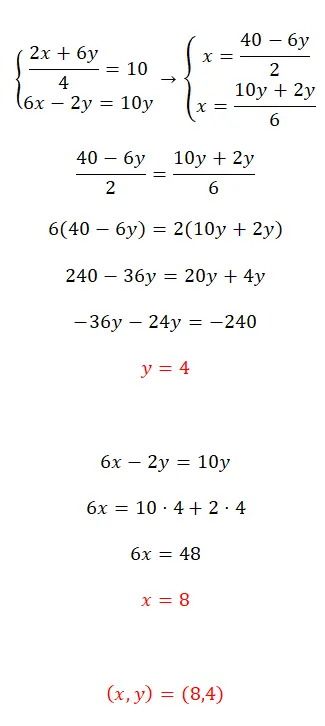
- Eerst isoleren we de x in beide vergelijkingen.
- Vervolgens matchen we de uitdrukkingen die we hebben verkregen.
- We verkrijgen de waarde van de eerste onbekende.
- We vervangen deze waarde in een van de twee initiële vergelijkingen en berekenen de tweede onbekende.
- Ten slotte drukken we de waarde van de twee vreemden uit.
Oefening 5
Los dit stelsel vergelijkingen op met behulp van de reductiemethode:
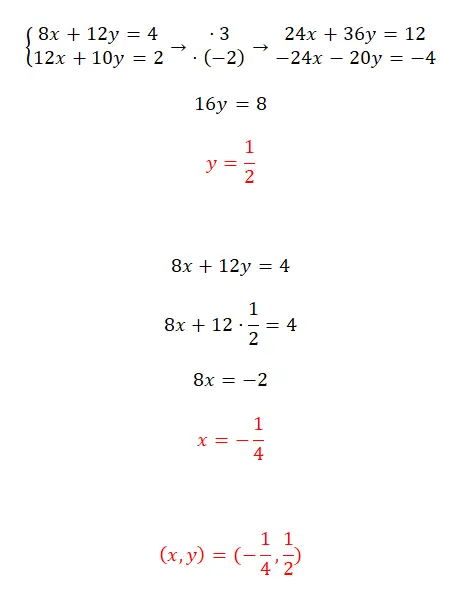
- Je moet zoeken naar twee getallen die het mogelijk maken dezelfde coëfficiënt te verkrijgen voor een van de twee variabelen in de twee vergelijkingen, maar met tegengesteld teken .
- Los vervolgens eenvoudigweg de vergelijking op die we verkrijgen door de twee verkregen uitdrukkingen bij elkaar op te tellen.
- Vervolgens vervangen we de y in een van de twee oorspronkelijke vergelijkingen om de x te berekenen.
- Ten slotte drukken we het resultaat van het systeem uit.
Oefening 6
Los dit stelsel vergelijkingen op met behulp van de reductiemethode:
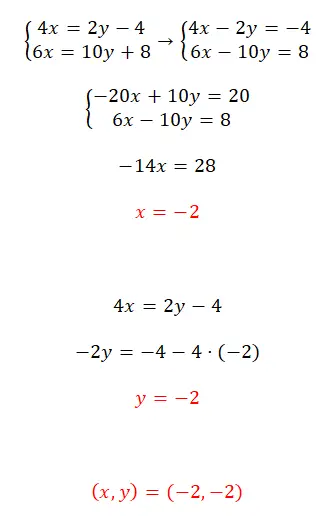
- We beginnen met het rangschikken van de vergelijkingen (alle variabelen naar links doorgeven).
- Vervolgens vermenigvuldigen we de eerste vergelijking met -5.
- We lossen de vergelijking die we verkrijgen op door de twee vergelijkingen op te tellen en de waarde van x te verkrijgen.
- We gebruiken deze bekende waarde om de waarde van y te verkrijgen.
- We drukken het resultaat van het systeem van vergelijkingen uit.
Oefening 7
Los dit stelsel vergelijkingen op met behulp van de substitutiemethode:
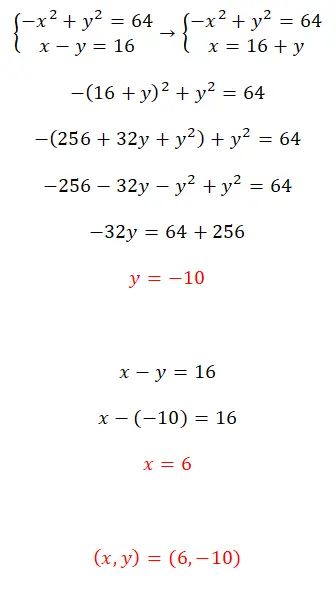
- Om dit systeem van niet-lineaire vergelijkingen op te lossen, raden we aan de substitutiemethode te gebruiken.
- Je construeert dus een vergelijking met de uitdrukking gelijk aan x.
- Je krijgt de waarde van de onbekende y.
- Je berekent de waarde van x met de waarde die je eerder hebt berekend.
- En je hebt beide waarden al.
Oefening 8
Los dit stelsel vergelijkingen op met de methode van jouw keuze:
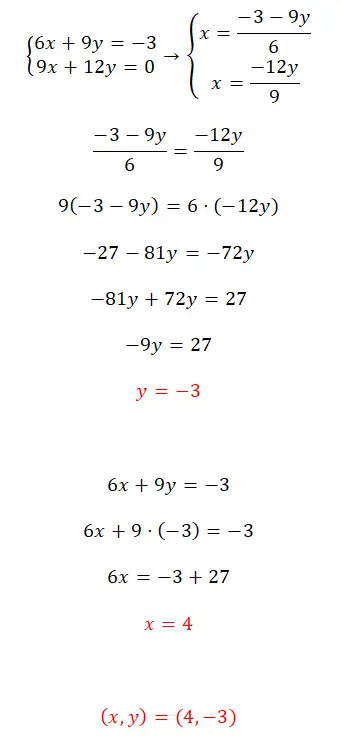
- In dit geval krijgen we een bepaald compatibel systeem te zien en zullen we het oplossen met behulp van de egalisatiemethode.
- Daarom lossen we x op in beide vergelijkingen en stellen we de twee resulterende uitdrukkingen gelijk.
- Nadat we de vergelijking hebben opgelost, krijgen we de waarde van y.
- We gebruiken deze waarde om de waarde van x te vinden.
- Ten slotte drukken we het resultaat van het systeem uit.