▷ Hoe weet ik of 3 (of meer) punten op één lijn liggen? ✅

Op deze pagina vindt u de uitleg van wat uitgelijnde punten zijn. U ziet ook alle beschikbare methoden om te bepalen of 3 (of meer) punten op één lijn liggen. En bovendien vind je er diverse voorbeelden en zelfs opgeloste oefeningen waarmee je kunt oefenen.

Wat betekent het dat de punten op één lijn liggen?

In de analytische meetkunde zijn drie of meer punten uitgelijnd als ze allemaal op dezelfde lijn liggen, dat wil zeggen als ze met elkaar verbonden kunnen worden door er een rechte lijn tussen te trekken.

Uiteraard zullen 2 punten altijd op één lijn liggen, omdat je altijd een lijn tussen twee punten kunt trekken. Drie punten hoeven echter niet op dezelfde lijn te liggen. Er zijn hoofdzakelijk twee methoden om te weten of 3 of meer punten op één lijn liggen:

Vectormethode : bestaat uit het kijken of de vectoren die de punten vormen proportioneel zijn.
Lijnvergelijkingsmethode : deze bestaat uit het bepalen of de punten tot dezelfde lijn behoren.

Hieronder vindt u de uitleg van elke procedure en voorbeelden, zodat u kunt beslissen welke het beste bij u past.

Hoe weet u of 3 (of meer) punten zijn uitgelijnd met de vectormethode?

Drie punten overwegen:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

De drie punten zijn uitgelijnd als de vectoren

$\vv{AB}$

$\vv{BC}$

ze hebben dezelfde richting, dat wil zeggen als hun componenten proportioneel zijn.

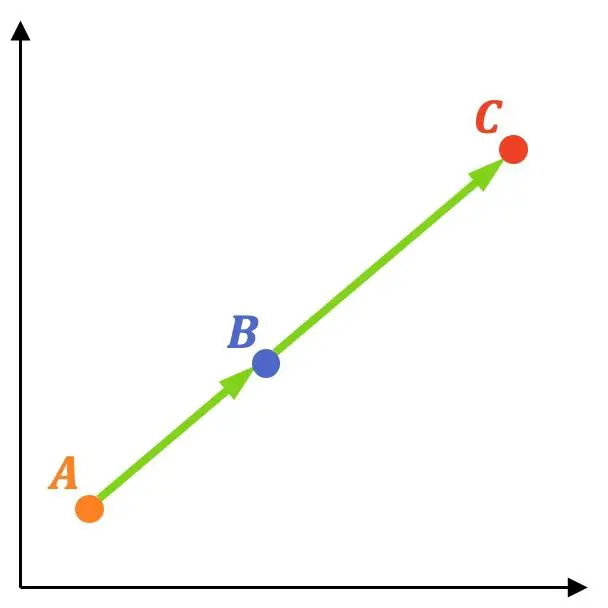
Laten we een voorbeeld bekijken van hoe dit wordt gedaan:

Bepaal of de volgende 3 punten op één lijn liggen:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Eerst berekenen we de vectoren tussen de punten. Het volstaat om twee verschillende vectoren te berekenen:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

En dan controleren we of de coördinaten van de vectoren proportioneel zijn:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Door de X-componenten en de Y-componenten van de twee vectoren te delen, verkrijgen we hetzelfde resultaat (-2), daarom hebben de vectoren dezelfde richting en daarom zijn de punten uitgelijnd .

Deze methode kan ook worden gebruikt om erachter te komen of drie of meer punten in de ruimte op één lijn liggen (in R3). Het enige dat hoeft te worden toegevoegd is om te controleren of de derde component van de twee vectoren (Z-component) ook proportioneel is.

Als dit artikel nuttig voor u is, zult u waarschijnlijk ook geïnteresseerd zijn om te weten hoe u het middelpunt tussen twee punten kunt berekenen, aangezien het vinden van het middelpunt van twee punten uiteraard een manier is om een derde punt te bepalen dat op één lijn ligt met de andere twee punten. Hoe het werkt, ziet u op de gelinkte pagina. Daarnaast ziet u ook stap voor stap opgeloste voorbeelden en oefeningen.

Hoe u kunt bepalen of 3 (of meer) punten op één lijn liggen met de vergelijkingsmethode met rechte lijnen

Zoals we zojuist in de vorige sectie hebben gezien, is een manier om de uitlijning van 3 of meer punten te bestuderen het gebruik van de vectoren die zich daartussen kunnen vormen. Een andere methode is om te beginnen met de vergelijking van een lijn:

Drie punten overwegen:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

De drie punten zijn uitgelijnd als ze allemaal tot dezelfde lijn behoren. Om te weten of drie of meer punten op één lijn liggen, moeten daarom de volgende stappen worden gevolgd:

Zoek de vergelijking van de lijn die door twee van de drie punten gaat.
Controleer of het derde punt ook bij de lijn hoort. In dit geval betekent dit dat de 3 punten op één lijn liggen. Als echter niet aan de voorwaarde wordt voldaan, betekent dit dat de punten niet op één lijn liggen.

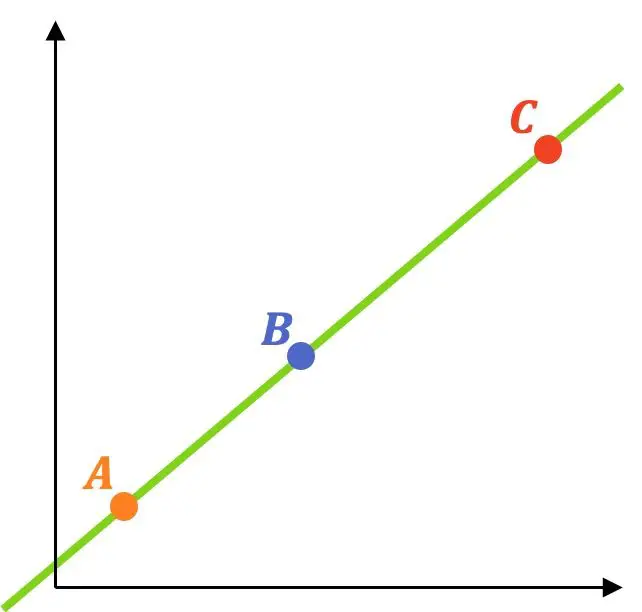
Als voorbeeld lossen we een oefening op met behulp van deze methode:

Controleer of de volgende 3 punten op één lijn liggen:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Allereerst moeten we de vergelijking berekenen van de lijn die door de punten A en B gaat. We vinden daarom de richtingsvector van de lijn:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Nu moet je de vergelijking van de lijn construeren, je kunt het gewenste type kiezen: parametrisch, impliciet, algemeen, enz. Maar in dit geval zullen we de continue vergelijking gebruiken. Dus de continue vergelijking van de lijn die door punt A en punt B gaat, is:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Zodra we de vergelijking van de lijn hebben, moeten we controleren of het andere punt ook tot dezelfde lijn behoort. Om dit te doen, vervangen we de coördinaten van punt C in de vergelijking van de lijn:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

We hebben een gelijkspel, dus het punt voldoet aan de vergelijking van de lijn. En daarom zijn de 3 punten collineair .

Opgemerkt moet worden dat een reeks uitgelijnde punten niet op gelijke afstanden hoeft te liggen, dat wil zeggen dat de afstand tussen verschillende uitgelijnde punten verschillend kan zijn. Het verschil tussen de twee concepten kun je zien in de uitleg van de afstand tussen twee punten (geometrie) , waar je ook voorbeelden en oefeningen kunt zien die stap voor stap worden opgelost.

Opgeloste oefeningen met uitgelijnde stippen

Oefening 1

Bepaal of de volgende 3 punten op één lijn liggen:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Zie de oplossing

We kunnen een van de twee methoden kiezen die we hebben gezien om het probleem op te lossen. In dit geval gebruiken we de vectormethode.

Eerst berekenen we de vectoren tussen de punten:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

En nu controleren we of de cartesische coördinaten van de vectoren proportioneel zijn:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Door de X-componenten en de Y-componenten van de twee vectoren door elkaar te delen krijgen we hetzelfde resultaat (-4), dus de vectoren hebben dezelfde richting. Feit dat aangeeft dat de punten op één lijn liggen .