Trigonometrische verhoudingen van een hoek zijn de verhoudingen verkregen uit de drie zijden van een rechthoekige driehoek. Met andere woorden, dit zijn de waarden die het resultaat zijn van het vergelijken van de drie zijden met behulp van quotiënten (verdelingen). Al moet worden opgemerkt dat deze redenen alleen bestaan bij rechthoekige driehoeken (driehoeken met een hoek van 90º).
Trigonometrische verhoudingen in een rechthoekige driehoek
De zes belangrijkste trigonometrische verhoudingen zijn: sinus, cosinus, tangens, cosecans, secans en cotangens. Vervolgens zullen we in detail uitleggen hoe elk van deze redenen wordt gedefinieerd en zullen we praten over de formule die hen kenmerkt. Om de volgende uitleg te begrijpen, zullen we rekening houden met de volgende rechthoekige driehoek:

Borst
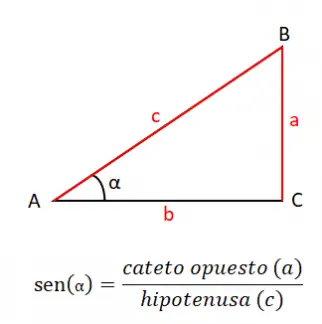
De sinus van een hoek (sin of sin) is gelijk aan het quotiënt van het tegenoverliggende been (a) tussen de hypotenusa (c), daarom is de sinusformule: sin (α) = a / c . Het is erg belangrijk om deze definitie van sinus te kennen, omdat deze de basis vormt van alle trigonometrie, samen met de andere redenen die we in deze sectie zullen bespreken.
Trav Het is vanuit de sinusstelling dat we elke zijde van de driehoek kunnen berekenen, we kunnen dit doen door de quotiënten van een bepaalde hoek te verbinden met de overeenkomstige zijde. Als we bijvoorbeeld zijde a willen berekenen en we hebben de zijdewaarden van de hoeken A en B, kunnen we dit doen met behulp van de formule: a / sin (A) = b / sin (B) . Door deze eenvoudige vergelijking op te lossen, verkrijgen we de waarde die overeenkomt met de variabele die we willen berekenen.
Cosinus
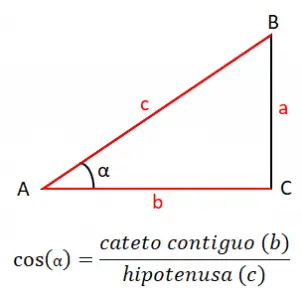
De cosinus van een hoek (cos) is gelijk aan het quotiënt van het aangrenzende been (b) tussen de hypotenusa (c), daarom is de cosinusformule: cos (α) = b / c . In dit geval bestaat de formule uit de twee zijden van de driehoek die in contact staan met de hoek die we willen bestuderen, in dit voorbeeld de hoek A of α.
Met cosinus hebben we ook een manier om de zijden van de driehoek te berekenen, wat voortkomt uit de cosinusstelling. Hierdoor kunnen we de zijkanten met de hoeken verbinden en krijgen we de volgende drie uitdrukkingen:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Raaklijn
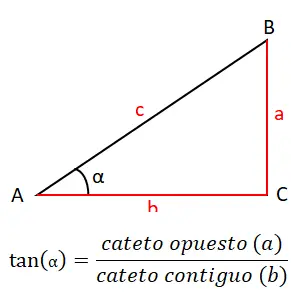
De derde belangrijkste reden, waarmee we de reeks oorspronkelijke redenen zullen afsluiten, is de raaklijn (tan of tg). Dit wordt berekend door te delen tussen het tegenoverliggende been (a) en het aangrenzende been (b). Daarom is de raaklijnformule: tan (α) = a / b . Hieronder kun je het grafisch zien:
De raaklijn heeft ook zijn eigen stelling, de raaklijnstelling genoemd. Hierdoor kunnen we de lengtes van twee zijden van een driehoek in verband brengen met de raaklijnen van de hoeken . De verklaring luidt als volgt: “het quotiënt van de som van twee zijden tussen hun aftrekkingen is gelijk aan het quotiënt tussen de raaklijn van het gemiddelde van de twee hoeken tegenover deze zijden en de raaklijn van de helft van het verschil hiervan” .
Afgeleide trigonometrische verhoudingen
Uit de drie trigonometrische verhoudingen die we zojuist hebben besproken, kunnen we andere afgeleide trigonometrische verhoudingen verkrijgen. Deze worden verkregen door de omgekeerde verhouding te nemen met betrekking tot de sinus, cosinus en tangens.
- Cosecans: is de inverse verhouding van sinus en wordt berekend met de formules: cosec (α) = c / a en cosec (α) = 1 / sin (α).
- Secans: is de inverse verhouding van de cosinus en wordt berekend met de formules: sec (α) = c / b en sec (α) = 1 / cos (α).
- Cotangens: is de inverse verhouding van de raaklijn en wordt berekend met de formules: cotg (α) = b / a en cotg (α) = 1 / tan (α).
Tabel met trigonometrische verhoudingen
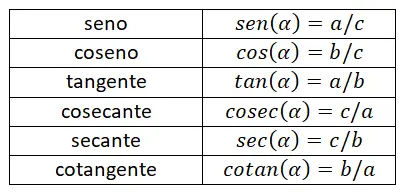
Hieronder ziet u een tabel met een samenvatting van alle redenen die tot nu toe zijn uitgelegd. Met deze tabel kunt u alle formules effectief onthouden, omdat u hierdoor gemakkelijk de verschillen tussen elke wiskundige uitdrukking kunt onderscheiden.
Trigonometrische verhoudingen in een cirkel
Een andere manier om trigonometrie te bestuderen is via de goniometrische omtrek of eenheidscirkel , deze omtrek heeft een straal gelijk aan 1 en de oorsprong is het punt (0, 0). De tekening bestaat uit een cirkel en een rechthoekige driehoek afgebeeld in de cirkel, preciezer gezegd, de hoek die we gaan bestuderen moet het oorspronkelijke punt raken.
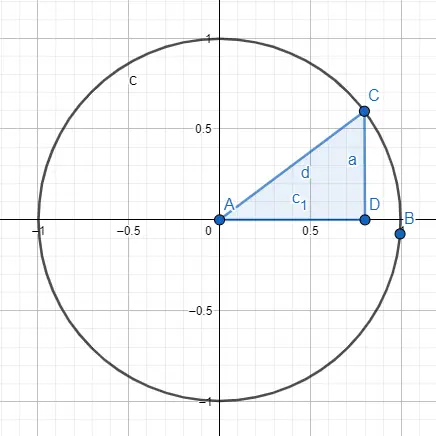
Als we dit beeld hebben, weten we dat de straal gelijk is aan de hypotenusa, die gelijk is aan 1. Dus als we de sinus en cosinus willen berekenen, gebruiken we de waarde van de straal en de waarde van de andere zijden van de driehoek. Om de sinus te berekenen, zullen we de volgende berekening uitvoeren: sin (A) = CD / AC = CD / straal = CD / 1 = CD , dus de sinus van A is a. Aan de andere kant, om de cosinus te berekenen, zullen we de berekening uitvoeren: cos (A) = AD / AC = AD / straal = AD / 1 = AD , daarom is de cosinus van A c1.
Het is heel belangrijk om twee dingen in gedachten te houden. De eerste is dat het gebruik van deze cirkel bij de studie van goniometrische verhoudingen te wijten is aan de noodzaak om met hoeken om te gaan die groter zijn dan die welke met de driehoek kunnen worden bestudeerd. De hoek van 150º kan bijvoorbeeld niet door een eenvoudige driehoek worden bestudeerd, omdat deze te groot is. En het tweede dat je in gedachten moet houden is dat sinus en cosinus nooit waarden groter dan 1 en kleiner dan -1 kunnen aannemen.
Teken van trigonometrische verhoudingen
Zoals we eerder zeiden, gebruiken we de goniometrische omtrek om met hoeken groter dan een driehoek om te gaan, om te gaan. Om dit te doen, vertegenwoordigen we een driehoek binnen de cirkel precies in een van de vier kwadranten die de omtrek verdelen, in de volgende afbeelding zie je de vier kwadranten weergegeven.
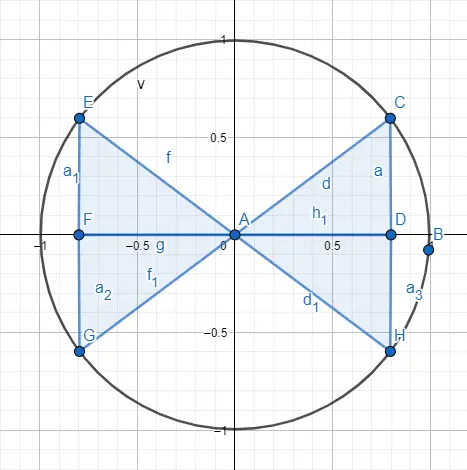
Dus om onderscheid te maken tussen een hoek van 30 en een van 210, die hetzelfde worden over de verdeling binnen de driehoek , zullen we een verdeling van tekens gebruiken volgens het kwadrant waarin de driehoek zich bevindt. Hieronder ziet u de borden die bij elk kwadrant horen en een getekend voorbeeld.
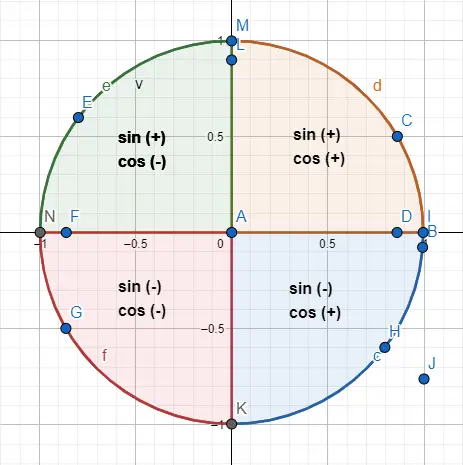
De hoeken 30º en 210º delen bijvoorbeeld dezelfde numerieke waarde , maar hun sinus en cosinus hebben tegengestelde tekens. Dus: sin(30) = 1/2 en cos(30) = √3/2, terwijl sin(210) = -1/2 en cos(210) = -√3/2. Om dit resultaat te bereiken vertegenwoordigen we de twee hoeken op de omtrek (afbeelding hieronder) en volgden we de aanwijzingen van de borden.
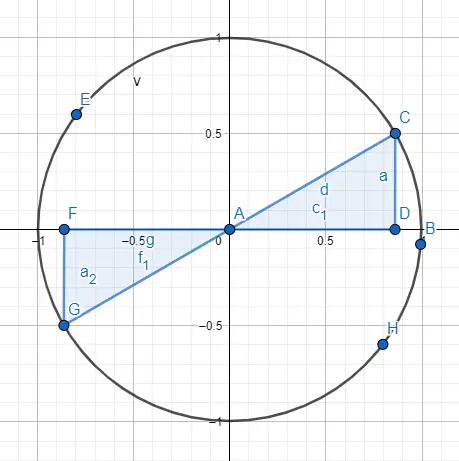
Tenslotte, hoe het mogelijk is om hoeken groter dan 360° te hebben, ook al lijkt dat misschien niet zo omdat de omtrek slechts 360° is. Maar als we een hoek van 750º willen oplossen, kunnen we reduceren tot een hoek tussen 0º en 360º. We delen eenvoudigweg 750 bij 360 en de rest is de resterende hoek, in het geval van 750º krijgen we een hoek van 30º.
Soorten hoeken afhankelijk van het kwadrant
Er zijn relaties tussen verschillende hoeken, waardoor we de verhoudingen kunnen berekenen trigonometrische waarden van alle hoeken die tot de cirkel behoren. Laten we deze redenen achterhalen van de reductie naar het eerste kwadrant . Dit betekent dat we vanuit een bepaalde hoek een vereenvoudiging maken naar het eerste kwadrant en vervolgens de bijbehorende tekens toepassen. Hieronder vindt u de verschillende procedures uitgelegd (afhankelijk van het kwadrant):
eerste kwadrant
In dit eerste kwadrant (0º – 90º) hoeven we alleen de trigonometrische verhouding op te lossen met de ons gegeven hoek. En als we naar de afbeelding kijken, hebben we beide eerder uitgelegd over symbolen, sinus en cosinus hebben een positief voor zich (het resultaat dat we krijgen wordt niet beïnvloed door het teken).
Reductie van het tweede kwadrant naar het eerste
In het tweede kwadrant (90° – 180°) hebben we te maken met aanvullende hoeken, wat betekent dat de twee hoeken samen 180° vormen. Daarom moeten we een reductie maken van het tweede kwadrant naar het eerste en dat doen we met de formule 180 – α = β , waarbij α de hoek van het eerste kwadrant is en β de oorspronkelijke hoek.
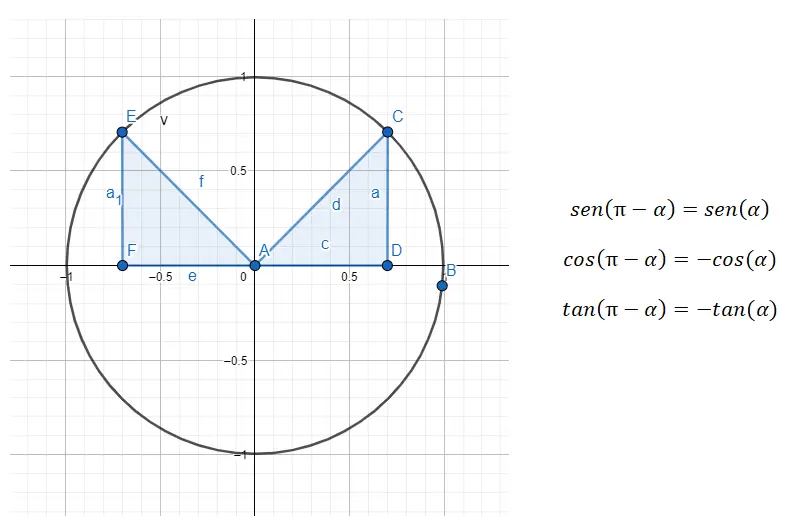
Als we bijvoorbeeld de hoek 135º krijgen (die bij het tweede kwadrant hoort), moeten we eerst de hoek uit het eerste kwadrant vinden die hiermee verband houdt. In dit voorbeeld is de hoek (α) die we zoeken 45º, aangezien 180 – 45 = 135. Dit zal dus waar zijn: sin (135) = sin (180 – 45) = sin (45), cos (135). ) = cos (180 – 45) = -cos (45) en tan (135) = tan (180 – 45) = -tan (45).
Reducering van het derde kwadrant tot het eerste
In het derde kwadrant (180º – 270º) hebben we te maken met hoeken die 80º van elkaar verschillen, wat betekent dat de hoeken 180º uit elkaar liggen. Dus als we van het derde kwadrant naar het eerste willen verkleinen, moeten we de formule 180 + α = β gebruiken, waarbij α de hoek van het eerste kwadrant is en β de oorspronkelijke hoek.
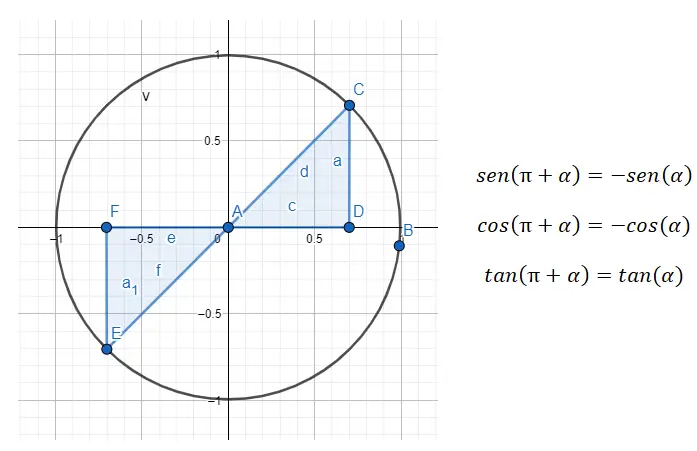
Als we bijvoorbeeld de hoek 225º krijgen (die bij het derde kwadrant hoort), moeten we de hoek van het eerste kwadrant vinden die daarmee overeenkomt. In het geval van 225º is de hoek (α) die we zoeken opnieuw 45º, aangezien 180 + 45 = 225. Dus sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) en tan (225) = tan (180 + 45) = tan (45) zal worden voldaan. ).
Reducering van het vierde kwadrant naar het eerste
In het vierde kwadrant (270º – 360º) hebben we te maken met tegengestelde hoeken, wat betekent dat de hoeken numeriek gelijk zijn, maar tegengestelde tekens hebben , zoals 30º en -30º (equivalent aan 330º, aangezien 360º – 30º = 330º) . Het is belangrijk om te onthouden dat tegengestelde hoeken kunnen worden geschreven als een positieve hoek en een negatieve hoek of als twee positieve hoeken (in het voorbeeld dat we zojuist hebben besproken, hebben we het verschil uitgelegd).
Dus als we een reductie willen uitvoeren van het vierde kwadrant naar het eerste, moeten we de formule 360 – α = β gebruiken, waarbij α de hoek van het eerste kwadrant is en β de oorspronkelijke hoek.
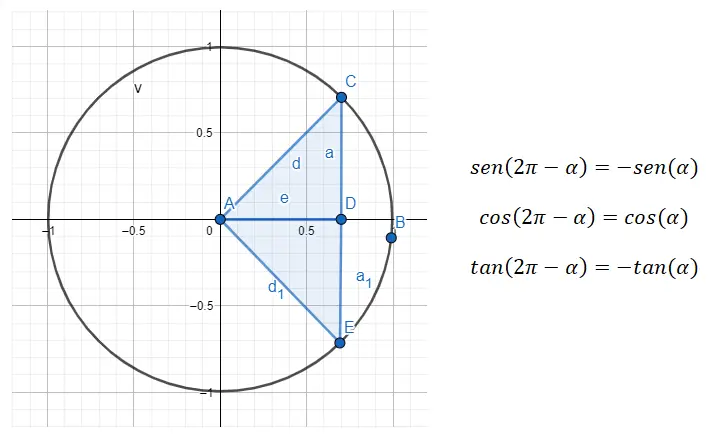
Als we bijvoorbeeld de hoek 315º krijgen (die bij het vierde kwadrant hoort), moeten we eerst de hoek van het eerste kwadrant vinden die hiermee verband houdt. In het geval van de hoek (α) die we zoeken, is deze nog steeds 45º, aangezien 360 – 45 = 315. Dus sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) en bruin (315) = bruin (360 – 45) = -bruin (45). Concluderend hebben we de hoeken gezien die zijn afgeleid van 45º van alle kwadranten.
Trigonometrische verhoudingen van de belangrijkste hoeken
Er zijn een aantal hoeken, opmerkelijke hoeken genoemd, die het meest voorkomen in de trigonometrie. Het wordt ten zeerste aanbevolen om uw goniometrische verhoudingen uit uw hoofd te kennen. Daarom hebben we hieronder een tabel gemaakt met de trigonometrische verhoudingen van deze hoeken en hun afgeleiden (dezelfde hoeken, maar met een verschil van 90, 180 of 270 graden):
| Hoek (°) | Hoek (rad) | Borst | Cosinus | Raaklijn |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 πrad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60º | 1/3 πrad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 πrad | -√2/2 | √2/2 | -1 |
Verband tussen trigonometrische verhoudingen
Er zijn verschillende manieren om de verschillende trigonometrische verhoudingen met elkaar in verband te brengen. Uit deze relaties verkrijgen we een soort gelijkheid tussen de verschillende trigonometrische functies, die we trigonometrische identiteiten noemen. Dankzij dit soort identiteiten kunnen we een verhouding berekenen op basis van elke andere. Opgemerkt moet worden dat er veel verschillende soorten trigonometrische identiteiten zijn, die worden geclassificeerd op basis van het type relatie dat de uitdrukking zelf ondersteunt.
Trigonometrische verhoudingen opgeloste problemen
Vervolgens bieden we je een reeks oefeningen aan waarmee je alle theorie die in dit artikel wordt uitgelegd in de praktijk kunt brengen. Onthoud dat als u op enig moment vastzit of vragen heeft, u het artikel kunt herlezen en bij een tweede lezing zult u alles zeker veel beter begrijpen. Dat gezegd hebbende, kun je beginnen met oefenen:
Oefening 1
Bereken de zes trigonometrische verhoudingen van de hoek 225º:
We beginnen met het berekenen van de hoek (α), die gelijk is aan: 180 + α = 225º, dus α = 45º.
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
bruin(225) = bruin(180 + 45) = bruin(45) = 1
Oefening 2
Bereken de zes trigonometrische verhoudingen van de hoek 120º:
We beginnen met het berekenen van de hoek (α), die gelijk is aan: 180 – α = 120º, dus α = 60º.
zonde(120) = zonde(180 – 60) = zonde(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
bruin(120) = bruin(180 – 60) = -bruin(60) = -√3
Oefening 3
Bereken de zes trigonometrische verhoudingen van de hoek 510º:
Voordat u begint, moet u de hoekverkleining uitvoeren: 510 / 360 = 1 slag en er blijft een hoek van 150 over. Vervolgens berekenen we de hoek (α), die gelijk is aan: 180 – α = 150, dus α = 30º.
zonde(150) = zonde(180 – 30) = zonde(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
bruin(150) = bruin(180 – 30) = -bruin(30) = -√3/3