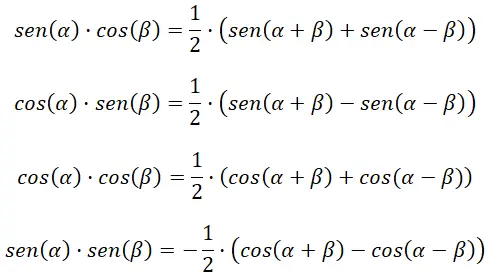Trigonometrische identiteiten zijn gelijkheden tussen verschillende trigonometrische functies. Dankzij deze trigonometrische equivalenties kunnen we een bepaalde trigonometrische verhouding afleiden op basis van elke andere. Daarom is het noodzakelijk om de formules van deze verhoudingen te kennen om de formules van trigonometrische identiteiten te begrijpen. Als u ze in uw geval niet kent, raden wij u aan de laatste link te bezoeken.
Tabel met trigonometrische identiteiten
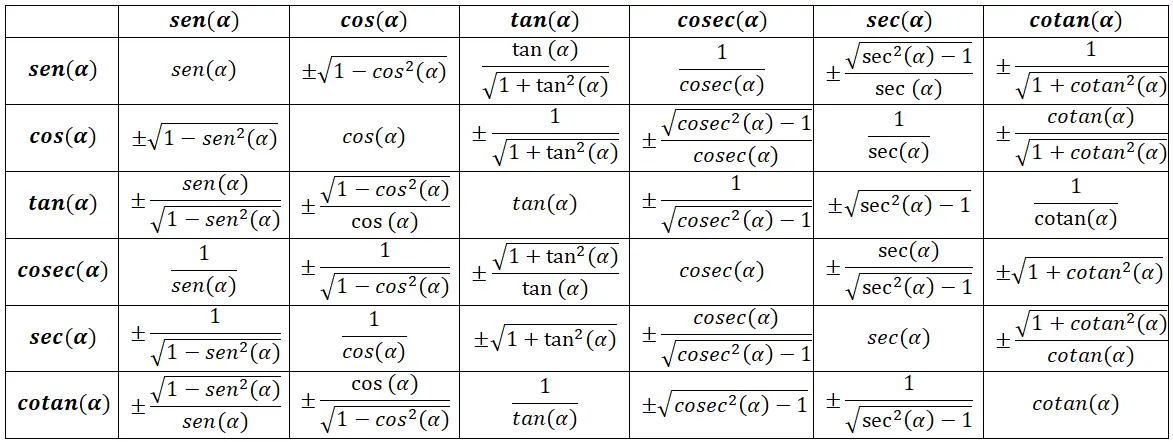
Fundamentele trigonometrische identiteiten
Er is een reeks fundamentele trigonometrische identiteiten die als de belangrijkste worden beschouwd omdat ze de theoretische basis vormen voor de andere. Deze zijn het meest gebruikelijk om te vinden en waarschijnlijk het gemakkelijkst te onthouden, omdat ze vrij intuïtief zijn. Houd er rekening mee dat alle formules gebaseerd zijn op de volgende afbeelding:

Fundamentele trigonometrische identiteit
De eerste identiteit van allemaal is wat bekend staat als de fundamentele trigonometrische identiteit , ook bekend als de relatie tussen sinus en cosinus. Hieronder vindt u het wiskundige bewijs: sin² (α) + cos² (α) = 1.
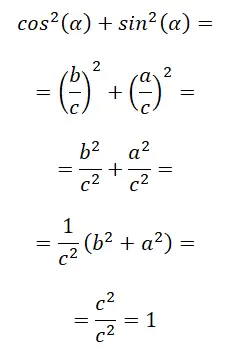
In de laatste stap passen we feitelijk de stelling van Pythagoras toe, omdat c² = a² + b², we houden dan c² / c² over wat gelijk is aan 1. Concluderend kunnen we stellen dat: sin² (α) + cos² (α) = 1.
Relatie tussen secans en raaklijn (secans in het kwadraat)
Ten tweede hebben we een trigonometrische identiteit die de secans relateert aan de raaklijn, de uitdrukking ervan is als volgt: sec² (α) = 1 + tan² (α) . In de volgende afbeelding ziet u enkele herinneringsformules waaruit deze identiteit bestaat en vervolgens de procedure die u moet volgen om tot de uiteindelijke formule te komen:
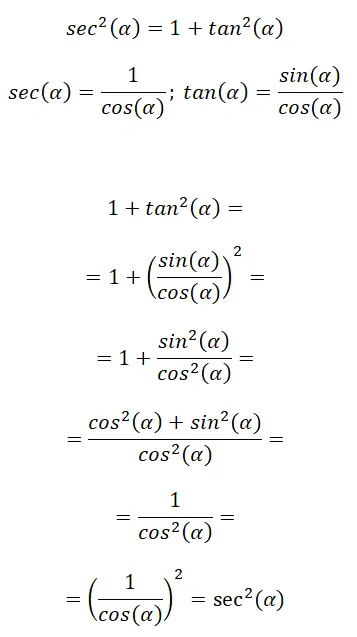
In dit geval gebruiken we de trig-verhoudingsformules om andere verhoudingen te vinden. Concluderend kunnen we zeggen dat: sec²(α) = 1 + tan²(α).
Relatie tussen cosecans en cotangens (cosecant kwadraat)
Uit de definitie van cosecans en cotangens kunnen we een verband vinden in de raaklijnformule. Dankzij dit kunnen we een andere trigonometrische identiteit afleiden: cosec² (α) = 1 + cotg² (α) .
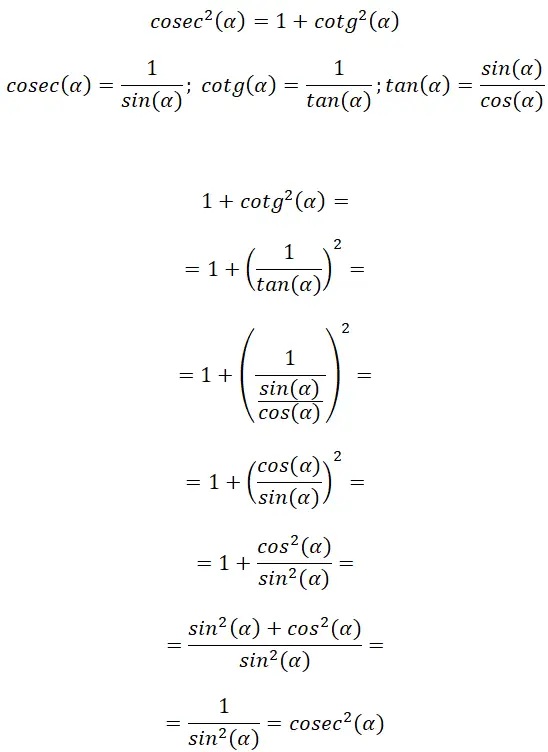
Met deze demonstratie kunnen we verifiëren dat: cosec² (α) = 1 + cotg² (α). Bovendien kunnen we zien dat deze relatie enige gelijkenis vertoont met de vorige, wat te wijten is aan de gelijkenis tussen raaklijn en cotangens.
Trigonometrische verhoudingen van somhoek en aftrekhoek
Hoeksom- of hoekaftrekverhoudingen zijn een soort identiteiten die worden verkregen door de trigonometrische verhoudingen te berekenen van het optellen of aftrekken van twee hoeken. Als we bijvoorbeeld de sinus van 90 + 60 willen berekenen, is er een reeks formules die deze berekening eenvoudiger maken. Hieronder staat een lijst met alle formules voor trigonometrische identiteiten van deze stijl:
Sinus van de som van de hoeken: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Sinus van hoekaftrekken: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Cosinus van de som van de hoeken: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Aftrekken van de hoekcosinus: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Raaklijn van de som van de hoeken: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Hoektangens aftrekken: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
Het is duidelijk dat het berekenen van de sinus van 150º eenvoudiger is dan het gebruik van de formules die we zojuist hebben uitgelegd om de sinus van (90º + 60º) te berekenen. Dus waarom zijn deze formules belangrijk? Het antwoord is dat deze identiteiten ons in staat stellen de trigonometrische verhoudingen van complexe hoeken vanuit eenvoudiger hoeken te berekenen. Als we dus de verhoudingen van opmerkelijke (meest relevante) hoeken onthouden, hoeven we de rekenmachine niet te gebruiken om de verhoudingen van complexere hoeken zoals 150º te berekenen.
Trigonometrische verhoudingen met dubbele hoek
Als we de goniometrische verhoudingen van een dubbele hoek (2α) willen berekenen, kunnen we dat doen aan de hand van een reeks identiteiten. Om precies te zijn, we kunnen dit doen met behulp van formules die sterk lijken op de formules die we zojuist in de vorige sectie hebben besproken. Omdat, als we β in α veranderen, we in de voorgaande uitdrukkingen (α + α) overhouden, wat equivalent is aan (2α). Met dit in gedachten kunnen we de volgende identiteiten afleiden:
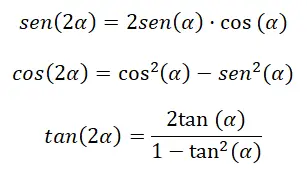
Hieronder kun je de demo’s bekijken:
Sinus van de dubbele hoek: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Cosinus van de dubbele hoek: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Dubbele raakhoek: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Trigonometrische verhoudingen van de halve hoek
Er zijn ook identiteiten waarmee we de trigonometrische verhoudingen van de halve hoek (α/2) kunnen berekenen:
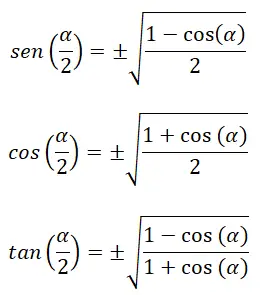
Onder de volgende reeds bekende formules:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
Als we β = α/2 maken, kunnen we deze identiteiten bewijzen door de twee uitdrukkingen af te trekken in het geval van sinus, ze op te tellen in het geval van cosinus, en de twee verkregen formules te delen (die van sinus en die van cosinus) in het geval van de raaklijn. Het blijft echter nodig om de verhouding die we willen berekenen te isoleren in de formules die we hieronder verkrijgen:
Halve sinushoek: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
Halve hoekcosinus: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
Trigonometrische verhoudingen van de drievoudige hoek
In het geval dat we een drievoudige hoek (3α) hebben, kunnen we ook bepaalde identiteiten gebruiken om hun trigonometrische verhoudingen te berekenen. Deze identiteiten komen voort uit de volgende formules die al zijn uitgelegd: dubbele hoekidentiteiten, somhoekidentiteiten en de fundamentele identiteit van trigonometrie.
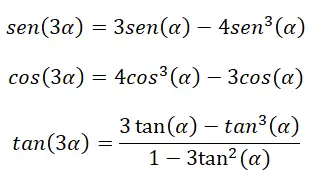
Om deze identiteiten te bewijzen, moeten we de hoeksomformules gebruiken:
Sinus van de som van de hoeken: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Cosinus van de som van de hoeken: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Dus als we de formules voor dubbele hoeken toepassen in de uitdrukkingen waar we het zojuist over hadden en de fundamentele identiteit van trigonometrie toepassen, kunnen we de identiteiten bewijzen. Het is de moeite waard te vermelden dat het gebruik van de fundamentele trigonometrische identiteit ons in staat stelt alle verhoudingen in de uitdrukking in één om te zetten. Dit is de reden waarom de formule voor de sinus van de drievoudige hoek alleen uit sinussen bestaat en die van de cosinus alleen cosinussen bevat. Hieronder ziet u de volledige procedure:
Sinus van de drievoudige hoek: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= zonde (α) · (1 – sin² (α)) – zonde³ (α) + 2 zonde (α) · (1 – sin² (α)) =
= zonde (α) – zonde³ (α) – zonde³ (α) + 2 zonde (α) – 2 zonde³ (α) =
= 3 zonde (α) – 4 zonde³ (α)
Cosinus van de drievoudige hoek: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Ten slotte kan de raaklijn van de drievoudige hoek op twee manieren worden berekend: de eerste door de sinusformule te delen door de cosinusformule en de tweede door de uitdrukking voor de raaklijn van de dubbele hoek te vervangen door de volgende formule voor de raaklijn van de somhoek: bruin (α + 2α) = (bruin (α) + bruin (2α)) ÷ (1 – bruin (α) bruin (2α)).
Trigonometrische identiteiten volgens hoektype
Het is belangrijk commentaar te geven op een reeks formules die in zekere zin regels zijn die de directe en snelle berekening van trigonometrische verhoudingen mogelijk maken. In feite kunnen ze ook als trigonometrische identiteiten worden beschouwd, omdat ze aan dezelfde kenmerken voldoen als alle uitdrukkingen waar we zojuist over gesproken hebben. Preciezer gezegd, deze formules stellen ons in staat de trigonometrische relaties van een hoek te bepalen op basis van de relatie die deze heeft met een andere hoek.
Complementaire hoeken
De complementaire hoeken (α en β ) zijn de hoeken waarvan de som gelijk is aan 90º, dus als we ze optellen, krijgen we een rechte hoek. Om te bepalen dat α de complementaire hoek van β is, moeten we een heel eenvoudige vergelijking oplossen: α = 90 – β . Als het resultaat van deze gelijkwaardigheid overeenkomt, kunnen we bevestigen dat ze complementair zijn. Dankzij deze identiteiten kunnen we de trigonometrische verhoudingen van de ene hoek afleiden van die van de andere.
Sinus van de complementaire hoek: sin (90º – α) = cos (α)
Cosinus van de complementaire hoek: cos (90º – α) = sin (α)
Raaklijn van de complementaire hoek: tan (90º – α) = cotan (α)
Cosecans van de complementaire hoek: cosec (90º – α) = sec (α)
Secans van de complementaire hoek: sec (90º – α) = cosec (α)
Cotangens van de complementaire hoek: cotan (90º – α) = tan (α)
extra hoeken
De aanvullende hoeken (α en β ) zijn die welke een som hebben gelijk aan 180º of π radialen, we kunnen daarom de formule α + β = 180º afleiden. Of, met andere woorden, als de aanvullende hoek van α β is, dan moet aan de volgende uitdrukking β = 180 – α worden voldaan. Dan kun je de lijst met identiteiten zien die we vanuit deze invalshoeken kunnen afleiden:
Sinus van de aanvullende hoek: sin (180º – α) = sin (α)
Cosinus van de extra hoek: cos (180º – α) = -cos (α)
Raaklijn van de aanvullende hoek: tan (180º – α) = -tan (α)
Cosecans van de extra hoek: cosec (180º – α) = cosec (α)
Secans van de aanvullende hoek: sec (180º – α) = -sec (α)
Cotangens van de aanvullende hoek: cotan (180º – α) = -cotan (α)
hoeken vervoegen
De geconjugeerde hoeken (α en β ) zijn de hoeken die een som hebben die gelijk is aan 360º of 2π radialen. Daarom kunnen we de formule α + β = 360º afleiden. En vanuit deze eerste formule kunnen we een van de hoeken als volgt uitdrukken in termen van de andere: α = 360º – β of β = 360º – α. We laten u nu de gelijkheden van geconjugeerde hoeken zien:
Sinus van de geconjugeerde hoek: sin (360º – α) = – sin (α)
Cosinus van de geconjugeerde hoek: cos (360º – α) = cos (α)
Raaklijn van de geconjugeerde hoek: tan (360º – α) = – tan (α)
Cosecans van de geconjugeerde hoek: cosec (360º – α) = – cosec (α)
Secans van de geconjugeerde hoek: sec (360º – α) = sec (α)
Cotangens van de geconjugeerde hoek: cotan (360º – α) = – cotan (α)
tegenovergestelde hoeken
Tegengestelde hoeken of negatieve hoeken (α en β ) zijn hoeken die dezelfde numerieke waarde hebben, maar verschillende tekens hebben. Een voorbeeld van dit type hoek is 30º en -30º. Houd er rekening mee dat het negatieve teken aangeeft dat de rotatie met de klok mee plaatsvindt, terwijl een positieve hoek tegen de klok in draait.
Sinus van de tegenovergestelde hoek: sin (-α) = – sin (α)
Cosinus van de tegenovergestelde hoek: cos (-α) = cos (α)
Raaklijn van de tegenovergestelde hoek: tan (-α) = – tan (α)
Cosecans van de tegenovergestelde hoek: cosec (-α) = – cosec (α)
Secans van de tegenovergestelde hoek: sec (-α) = sec (α)
Cotangens van de tegenovergestelde hoek: cotan (-α) = – cotan (α)
Hoeken die afwijken van 90º of hoeken plus/minus π/2
Hoeken die 90º verschillen of hoeken plus/minus π/2 (α en β ) zijn hoeken met een verschil van 90º. Daarom kunnen ze worden uitgedrukt als β – α = 90º, waarbij β 90º groter is dan α . Deze hoeken hebben ook een reeks formules die de trigonometrische verhoudingen van de twee hoeken met elkaar in verband brengen.
Sinus van de hoek die afwijkt van 90º: sin (90º + α) = cos (α)
Cosinus van de hoek die afwijkt van 90º: cos (90º + α) = -sin (α)
Raaklijn van de hoek die afwijkt van 90º: tan (90º + α) = – cotan (α)
Cosecans van de hoek die afwijkt van 90º: cosec (90º + α) = sec (α)
Secans van de hoek die afwijkt van 90º: sec (90º + α) = -cosec (α)
Cotangens van de hoek die afwijkt van 90º: cotan (90º + α) = -cotan (α)
Hoeken die afwijken van 180º of hoeken plus/minus π
De plus/minus-hoeken π (α en β ) zijn equivalent aan hoeken die 180º verschillen. Daarom kunnen ze worden uitgedrukt met behulp van de volgende formule: β – α = 180º, waarbij β 180º groter is dan α . Vervolgens laten we u de goniometrische identiteiten zien die de goniometrische verhoudingen van deze hoeken met elkaar in verband brengen:
Sinus van de hoek die afwijkt van 180º: sin (180º + α ) = -sin ( α )
Cosinus van de hoek die afwijkt van 180º: cos (180º + α ) = -cos ( α )
Raaklijn van de hoek die afwijkt van 180º: tan (180º + α ) = tan ( α )
Cosecans van de hoek die afwijkt van 180º: cosec (180º + α ) = -cosec ( α )
Secans van de hoek die afwijkt van 180º: sec (180º + α ) = -sec ( α )
Cotangens van de hoek die afwijkt van 180º: cotan (180º + α ) = cotan ( α )
Transformaties van trigonometrische verhoudingen
Ten slotte zijn er trigonometrische identiteiten die ons in staat stellen een bepaalde trigonometrische verhouding uit te drukken door middel van andere bewerkingen . Dus als we een som van verhoudingen hebben en deze als een product willen uitdrukken, kunnen we onze toevlucht nemen tot deze formules. Hoewel er helaas geen uitdrukking is voor elke rekenkundige bewerking, kun je alleen van optellen of aftrekken naar product gaan en omgekeerd .
Converteer optellen of aftrekken naar product
De volgende vier formules helpen ons bij het berekenen van het optellen en aftrekken van goniometrische functies:
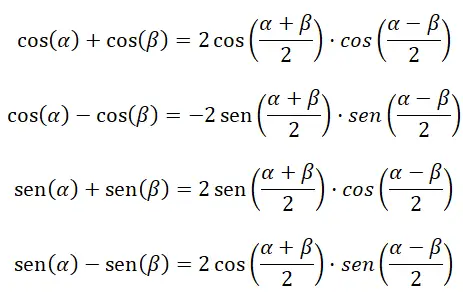
Transformeer het product in optellen of aftrekken
De volgende vier formules helpen ons de producten van trigonometrische functies te berekenen: