Hier leert u hoe u trigonometrische limieten oplost. Je zult verschillende voorbeelden van limieten van goniometrische functies kunnen zien en zelfs oefenen met opgeloste stapsgewijze oefeningen over goniometrische limieten.
Wat zijn trigonometrische limieten?
Trigonometrische limieten zijn limieten die worden berekend op basis van goniometrische functies. Om trigonometrische limieten op te lossen, moet een voorbereidende procedure worden toegepast, omdat deze doorgaans aanleiding geven tot onbepaaldheid.
Bovendien bestaan er geen oneindige limieten voor trigonometrische functies, omdat het periodieke functies zijn. Dat wil zeggen dat de grafieken voortdurend periodiek worden herhaald zonder naar een specifieke waarde te neigen.
Trigonometrische limietformules
Alle trigonometrische limieten worden berekend op basis van de volgende twee formules:
![]()
Als we de limiet proberen te berekenen door middel van substitutie, verkrijgen we de nulbepaaldheid tussen nul:
![]()
Maar deze trigonometrische formule kan worden gedemonstreerd door waarden te berekenen van de dichtstbijzijnde functie en dichter bij x=0 (hoeken in radialen).
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
De twee laterale grenzen van de goniometrische functie geven 1, dus de limiet op het punt x=0 is 1:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
De trigonometrische limiet van de sinus van x gedeeld door x, aangezien x naar 0 neigt, is dus gelijk aan 1.
Deze formule kan ook voor verschillende hoeken worden toegepast:
![]()
![]()
Als we proberen de limiet te vinden door directe substitutie, krijgen we de onbepaalde vorm nul tussen nul:
![]()
Maar we kunnen de gelijkheid controleren aan de hand van de bovenstaande formule. Om dit te doen, moet je eerst de teller en de noemer van de breuk vermenigvuldigen met 1 plus de cosinus van x:
![]()
We hebben nu een opmerkelijke identiteit in de teller van de breuk, dus we kunnen deze vereenvoudigen:
![]()
![]()
Vertrekkend van de fundamentele trigonometrische identiteit herschrijven we de teller:
![]()
![]()
We kunnen de breuk daarom omzetten in een product van breuken:
![]()
![]()
Met behulp van de eigenschappen van limieten kunnen we de bovenstaande uitdrukking omzetten in een product van limieten:
![]()
Met behulp van de hierboven gedemonstreerde formule kunnen we de trigonometrische limiet eenvoudig vereenvoudigen:
![]()
![]()
![]()
En ten slotte berekenen we de resulterende limiet:
![]()
Daarom wordt de trigonometrische limietformule geverifieerd:
![]()
Net als de andere formule kan deze ook voor meerdere hoeken worden gebruikt:
![]()
Om trigonometrische limieten op te lossen, moeten we daarom rekenkunde gebruiken om de functies te transformeren en soortgelijke uitdrukkingen te verkrijgen. Op deze manier kunnen we een van de twee formules gebruiken en de waarde van de limiet vinden.
Aan de andere kant moeten we soms bepaalde trigonometrische identiteiten toepassen, dus laten we alle onderstaande formules aan u over
Formule die de drie belangrijkste trigonometrische verhoudingen met elkaar verbindt:
![]()
Fundamentele trigonometrische identiteit:
![]()
Trigonometrische relaties afgeleid van de fundamentele:
![]()
![]()
Tegenovergestelde hoeken:
![]()
![]()
![]()
Som van twee hoeken:
![]()
![]()
![]()
Verschil van twee hoeken:
![]()
![]()
![]()
Dubbele hoek:
![]()
![]()
![]()
Halve hoek:
![]()
![]()
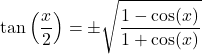
Optellen en aftrekken van sinus en cosinus:
![]()
![]()
![]()
![]()
Product van sinussen en cosinussen:
![]()
![]()
![]()
Om u precies te laten zien hoe trigonometrische limieten worden berekend, hebben we hieronder een stapsgewijs voorbeeld samengesteld.
Voorbeeld van trigonometrische limiet
Laten we eens kijken hoe een trigonometrische limiet wordt opgelost aan de hand van het volgende voorbeeld:
![]()
Als we proberen de trigonometrische limiet te berekenen, verkrijgen we de onbepaaldheid van nul tussen nul:
![]()
➤ Zie: nulgrenzen tussen nul
Het is daarom noodzakelijk om de trigonometrische functie te transformeren om de limiet op te lossen. De tangensfunctie is gelijk aan de sinus gedeeld door de cosinus, dus:
![]()
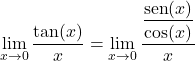
We kunnen de functie nu als een product uitdrukken door de eigenschappen van breuken toe te passen:
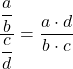
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
Met behulp van de eigenschappen van limieten kunnen we de limiet van twee vermenigvuldigde functies omzetten naar het product van twee limieten:
![]()
Zoals we hierboven hebben laten zien, geeft de eerste trigonometrische limiet 1:
![]()
![]()
Voer dus gewoon de volgende berekening uit:
![]()
Opgeloste oefeningen over trigonometrische limieten
Oefening 1
Los de volgende trigonometrische limiet op:
![]()
Eerst proberen we de trigonometrische limiet te berekenen door directe evaluatie:
![]()
Maar we krijgen nul boven nul onbepaaldheid. We moeten dus transformaties op de functie toepassen.
Eerst laten we de x in de noemer staan door het volgende te doen:
![]()
Nu vermenigvuldigen en delen we de breuk door 4 om een uitdrukking te verkrijgen waarmee de eerste formule voor trigonometrische limieten kan worden toegepast:
![]()
Ten slotte passen we de formule toe die we aan het begin hebben gezien en lossen we de trigonometrische limiet op:
![]()
![]()
Oefening 2
Bereken de volgende trigonometrische limiet:
![]()
Eerst proberen we de trigonometrische limiet te vinden:
![]()
Maar de onbepaalde vorm nul komt overeen met nul is bereikt.
Vervolgens zetten we de raaklijn om in een quotiënt van de sinus en de cosinus:
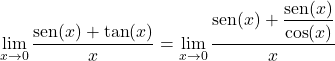
We vermenigvuldigen en delen door de cosinus van x:
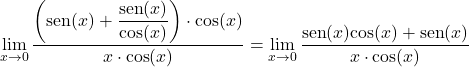
We nemen een gemeenschappelijke factor in de teller en scheiden de trigonometrische limiet in tweeën:
![]()
En tenslotte vinden we het resultaat van de trigonometrische limiet:
![]()
Oefening 3
Los de limiet van de volgende trigonometrische functie op als x nul nadert:
![]()
Door de directe berekening uit te voeren, verkrijgen we de onbepaalde limiet 0 tussen 0:
![]()
We zullen dus de limiet vereenvoudigen door elke term te delen door de tangens van x:
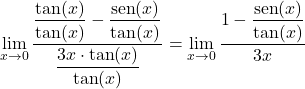
Ten tweede kunnen we uit de fundamentele trigonometrische identiteit afleiden dat de breuk van de teller equivalent is aan de cosinus van x:
![]()
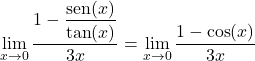
En door de tweede formule toe te passen die wordt gedemonstreerd in de theorie van trigonometrische limieten, kunnen we de limiet gemakkelijk oplossen:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
Oefening 4
Bepaal de oplossing van de volgende trigonometrische limiet op het punt x=0:
![]()
Als we de limiet proberen op te lossen, vinden we de onbepaalde vorm 0/0:
![]()
De algebraïsche uitdrukking voor de teller kan worden herschreven met behulp van de trigonometrische identiteit van de sinus van een dubbele hoek:
![]()
![]()
Laten we nu de limiet van de trigonometrische functie in een product scheiden:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
En ten slotte lossen we de trigonometrische limiet op door de eigenschappen van limieten toe te passen:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)