Tartaglia (of Pascal) driehoek

Op deze pagina leggen we uit wat de Tartaglia-driehoek, ook wel de driehoek van Pascal genoemd, is. We leren hoe we de Tartaglia (of Pascal) driehoek wiskundig kunnen construeren, evenals waarvoor deze wordt gebruikt en wat al zijn eigenschappen zijn. Ten slotte laten we zien hoe en wanneer deze zeer belangrijke driehoek tot stand is gekomen.

Wat is de driehoek van Tartaglia (of Pascal)?

De Tartaglia-driehoek , ook wel de driehoek van Pascal genoemd, is een wiskundige weergave van geordende gehele getallen in de vorm van een driehoek. De Tartaglia (of Pascal) driehoek wordt gebruikt om wiskundige berekeningen te maken.

Dit is de definitie van de Tartaglia- of Pascal-driehoek, maar je begrijpt het concept zeker beter met een afbeelding van de driehoek:

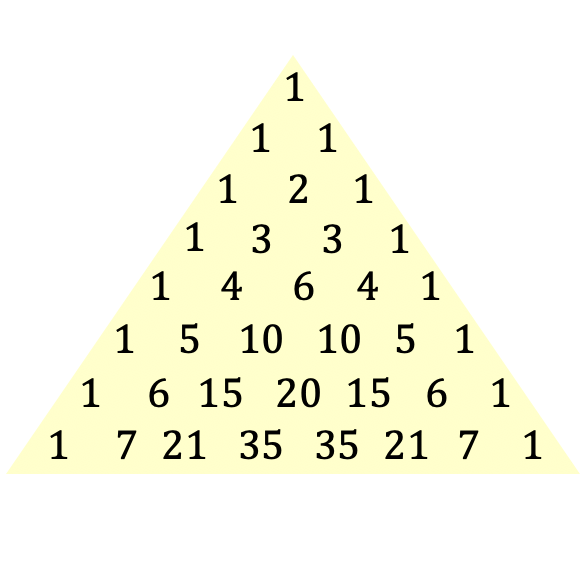
De driehoek van Tartaglia wordt ook wel de driehoek van Pascal genoemd, naar de Franse filosoof en wiskundige Blaise Pascal, die deze driehoekige uitdrukking in 1654 introduceerde, hoewel deze driehoek al sinds de oudheid bekend is. Hieronder gaan we dieper in op de geschiedenis van deze specifieke driehoek.

Hoe is de driehoek van Tartaglia of Pascal opgebouwd?

Zoals je in de driehoek van Pascal (of Tartaglia) hebt gezien, zijn er veel getallen, maar dat betekent niet dat we ze uit ons hoofd moeten kennen (godzijdank). Er is een formule waarmee je eenvoudig alle getallen in de Pascal- of Tartaglia-driehoek kunt vinden, je hoeft alleen maar eenvoudige sommen op te lossen.

Om de Tartaglia- of Pascal-driehoek te construeren, begin je bovenaan de driehoek, wat altijd een 1 is, en vervolgens worden de lijnen eronder berekend. Elk getal in de volgende regels is de som van de twee getallen er direct boven, behalve de uiteinden van de regels die altijd 1 zijn.

Daarom kun je zoveel lijnen van de Tartaglia-driehoek berekenen als je wilt, omdat je achtereenvolgens lijnen kunt toevoegen door de getallen op te tellen.

Waar wordt de driehoek van Tartaglia of Pascal voor gebruikt?

Weten hoe je de Tartaglia-driehoek moet construeren is heel goed, maar… waar wordt deze rekenkundige driehoek voor gebruikt? Welnu, de driehoek van Tartaglia (of Pascal) heeft veel toepassingen in de wiskunde, vooral op het gebied van de algebra.

combinatorische getallen

Allereerst wordt de Tartaglia-driehoek gebruikt om direct combinatorische getallen te berekenen, ook wel binomiale coëfficiënten genoemd. Als u niet weet wat dit soort operaties zijn, kunt u ernaar zoeken op onze website (we hebben een zoekmachine rechtsboven) omdat we een gedetailleerd artikel hebben geschreven waarin we uitleggen hoe ze worden opgelost en u daar. vindt u ook voorbeelden en oefeningen die stap voor stap worden opgelost. Maar samengevat is de algebraïsche uitdrukking voor een combinatorisch getal als volgt:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Welnu, alle combinatorische getallen kunnen eenvoudig worden bepaald met de Tartaglia-driehoek, omdat de oplossing van elke binomiale coëfficiënt equivalent is aan een getal van deze driehoekige uitdrukking, zoals weergegeven in de volgende afbeelding:

combinatorische getallen van de Tartaglia- of Pascal-driehoek

Bijvoorbeeld het combinatorische getal

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

geeft 6 terug, omdat er in de Tartaglia-driehoek een 6 staat.

Dus als je weet hoe je de driehoek van Tartaglia of Pascal moet construeren, kun je elk combinatorisch getal snel berekenen zonder de formule ervan te gebruiken.

De binomiaal van Newton

Een ander gebruik van de Tartaglia (of Pascal) driehoek is om machten van binomialen te kunnen berekenen (klik op deze link om erachter te komen wat een binomiaal is).

Een voorbeeld van de versterking van een binomiaal zijn opmerkelijke identiteiten, zoals:

$(a+b)^2$

Opmerkelijke identiteiten zijn erg belangrijk voor de wiskunde, omdat ze ons in staat stellen veel berekeningen op te slaan en ingewikkelde bewerkingen direct en snel op te lossen. Daarom raden we je aan de volgende link te bekijken als je nog steeds niet weet wat Opmerkelijke Identiteiten zijn .

Zoals je in de vorige link hebt gezien, kunnen opmerkelijke producten rechtstreeks worden opgelost met hun formules. Maar… wat gebeurt er als het paar wordt verhoogd naar de kubus of naar een hoger niveau?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Welnu, deze binomialen kunnen op een heel eenvoudige manier worden berekend met de Tartaglia-driehoek dankzij de binomiale stelling (of de binominale stelling van Newton). Eenmaal onder de knie, is de methode snel toe te passen, om het goed uit te leggen heb je een hele pagina nodig. Dus als je meer geïnteresseerd bent in het oplossen van dit soort binomialen, klik dan op de gelinkte pagina en je kunt zien hoe je dat doet.

Combinatoriek

De driehoek van Tartaglia, of de driehoek van Pascal, kan ook worden gebruikt om combinaties en kansen te bepalen.

Als we ooit een probleem tegenkomen waarbij we moeten bepalen hoeveel verschillende groepen uit een groep kunnen worden gemaakt, ongeacht de volgorde, kunnen we de Tartaglia-driehoek gebruiken.

Als we bijvoorbeeld 5 kaarten hebben, om te weten op hoeveel manieren we er 3 kunnen kiezen, ga dan naar de derde kolom (de eerste kolom is nul) van de vijfde rij (de eerste rij is ook rij 0) van de Tartaglia-driehoek. Het getal op deze positie (10) komt overeen met het aantal mogelijkheden dat er is om 3 kaarten te kiezen.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Dus uit 5 kaarten kunnen 10 verschillende groepen van drie kaarten worden gevormd.

Eigenschappen van de Tartaglia- of Pascal-driehoek

De Tartaglia-driehoek, ook wel de driehoek van Pascal genoemd, heeft de volgende kenmerken:

De Tartaglia (of Pascal) driehoek is symmetrisch, dat wil zeggen dat de verticale lijn die de hele driehoek in twee gelijke gelijkzijdige driehoeken verdeelt, een symmetrieas is.

De horizontale som van alle getallen in een willekeurige lijn van de driehoek van Pascal is gelijk aan een macht van 2.

eigenschappen van de driehoek van tartaglia of pascal

De diagonalen van de Tartaglia-driehoek zijn ook belangrijk: de getallen op de eerste diagonaal (buitenste diagonaal) zijn enen, de tweede diagonaal wordt gevormd door de reeks van alle natuurlijke getallen, de derde diagonaal komt overeen met driehoekige getallen en de vierde diagonaal is samengesteld van tetragonale (of tetraëdrische) getallen.

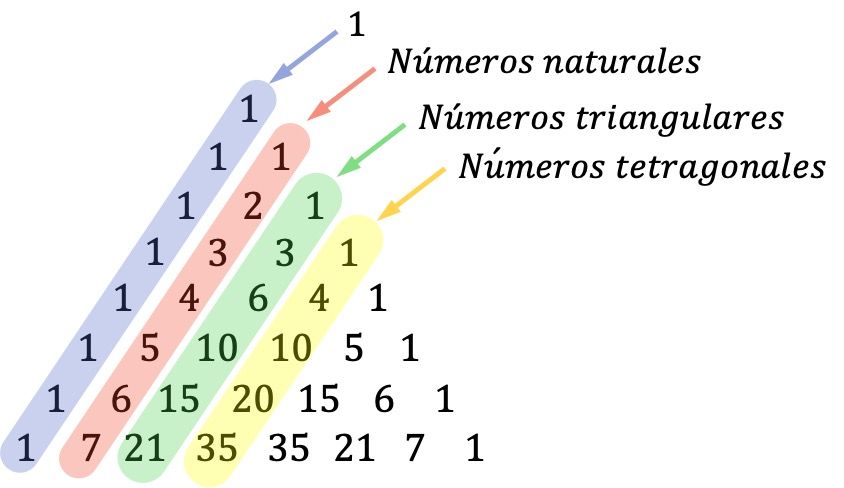
tartaglia-driehoek of pascal driehoekige en tetragonale getallen

Driehoekige getallen zijn getallen die kunnen worden weergegeven in de vorm van een driehoek. En tetragonale getallen zijn getallen die driehoekige piramides vormen.

Als je niet weet wat driehoekige of tetragonale getallen zijn, gebeurt er niets, het is gewoon een curiosum over de Tartaglia-driehoek. U moet echter de betekenis kennen van natuurlijke getallen (getallen die worden gebruikt om elementen te tellen).

Als het eerste getal in een rij een priemgetal is, met uitzondering van het getal 1, zijn alle getallen op diezelfde regel deelbaar door dat getal. In de achtste rij (1-7-21-35-35-21-7-1) kunnen bijvoorbeeld de getallen 7, 21 en 35 worden gedeeld door 7 (zeven is een priemgetal).

Een andere bijzonderheid van de Tartaglia-driehoek is dat de Fibonacci-reeks kan worden gevonden door de diagonalen op een bepaalde manier op te tellen:

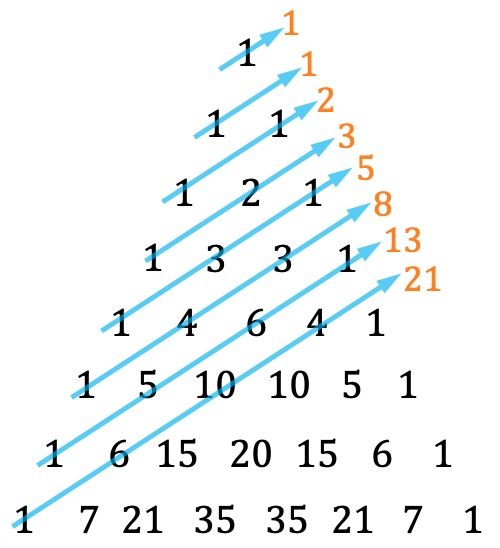
tartaglia of pascal driehoek fibonacci-reeks

Onthoud dat elke term van de Fibonacci-reeks gelijk is aan de som van de twee voorgaande, waarbij de eerste twee termen 1 en 1 zijn. De getallen die tot de Fibonacci-reeks behoren zijn dus: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…

Als we twee opeenvolgende getallen uit de derde diagonaal van de driehoek van Pascal (1-3-6-10-15-…) optellen, krijgen we een perfect vierkant (1, 4, 9, 16, 25,…).

Als we de even getallen van de driehoek van Pascal in één kleur schilderen en de oneven getallen in een andere kleur, krijgen we de figuur van de Sierpinski-driehoek, een beroemde geometrische reeks. Hieronder zie je de driehoek van Pascal met een hoogte van 512, weergegeven met de oneven getallen zwart gekleurd en de even getallen wit gekleurd:

sierpinski-driehoek van tataglia of pascal-driehoek

Het vermoeden van de Singmaster zegt dat het aantal keren dat elk getal groter dan 1 voorkomt eindig is. Of met andere woorden: hoewel het aantal rijen in de Tartaglia-driehoek oneindig is, is het aantal keren dat elk getal voorkomt, behalve 1, eindig. Uit curiositeit blijkt dat het getal 3003 het enige getal is waarvan tot nu toe bekend is dat het tot acht keer in de driehoek voorkomt.

Geschiedenis van de Tartaglia- of Pascal-driehoek

Nu we weten hoe de Tartaglia-driehoek eruit ziet, laten we eens kijken wanneer deze zeer speciale wiskundige driehoek werd uitgevonden.

Hoewel de naam van de rekendriehoek vooral wordt toegeschreven aan de beroemde wetenschappers Tartaglia en Pascal, werd deze algebraïsche driehoek al eerder gebruikt.

Het eerste record van een driehoek gevormd door binominale coëfficiënten dateert uit de 10e eeuw in India. De Perzen begonnen echter de eigenschappen ervan te bestuderen, met name de wiskundigen Al-Karaji (953-1029) en Omar Khayyam (1048-1131). Dit is de reden waarom het in Iran gepopulariseerd werd als de Khayyam-Pascal-driehoek of zelfs simpelweg de Khayyam-driehoek .

Deze driehoek werd in de 11e eeuw door de wiskundige Jia Xian in China geïntroduceerd, maar het was later in de 13e eeuw dat Yang Hui hem introduceerde als de rekenkundige driehoek . En om deze reden noemen ze het in het Aziatische land de Yang Hui-driehoek .

De wiskundige driehoek bereikte het Europese continent later via de Duitser Petrus Apianus, specifiek gepubliceerd in het jaar 1527 in zijn boek Rechnung . Van daaruit bestudeerde de beroemde Italiaanse algebraïst Niccolò Fontana Tartaglia de driehoek diepgaand tijdens de eerste helft van de 16e eeuw, en ter ere van hem staat deze in landen als Italië bekend als de Tartaglia-driehoek.

Ten slotte demonstreerde de Fransman Blaise Pascal veel van de eigenschappen van de bestudeerde driehoek in zijn publicatie van de Verhandeling over de Arithmetische Driehoek in 1654, vandaar de naam Pascal’s driehoek. Opgemerkt moet worden dat sommige van deze eigenschappen al bekend waren, maar het was Pascal die de demonstratie ervan uitvoerde door middel van wiskundige inductie.

De driehoek van tartaglia (of pascal).