Op deze pagina vind je alles over de raaklijnfunctie: wat is het, wat is de formule, hoe je het in een grafiek weergeeft, de kenmerken van de functie, de periode ervan, enz. Bovendien kunt u voorbeelden van raaklijnfuncties zien om het concept volledig te begrijpen. Hij legt zelfs de raaklijnstelling uit en de relaties die de raaklijnfunctie heeft met andere trigonometrische relaties.
Tangens-functieformule
De raaklijnfunctie van een hoek α is een trigonometrische functie waarvan de formule wordt gedefinieerd als de verhouding tussen de tegenoverliggende tak en de aangrenzende (of aangrenzende) tak van een rechthoekige driehoek (driehoek met een rechte hoek).

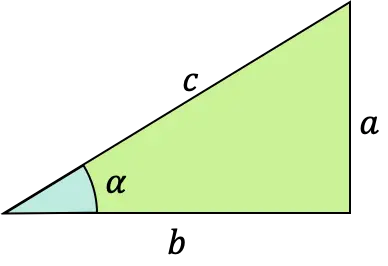
Dit type wiskundige functie wordt ook wel een tangentoïde, tangenoïde of tangentiële functie genoemd. En het kan worden uitgedrukt met de afkorting “tg” of zelfs “tan”.
De tangensfunctie is een van de drie bekendste trigonometrische verhoudingen, samen met de sinus en cosinus van een hoek.
Karakteristieke waarden van de raaklijnfunctie
Er zijn bepaalde hoeken die vaak worden herhaald en daarom is het handig om de waarde van de raaklijnfunctie bij deze hoeken te kennen:
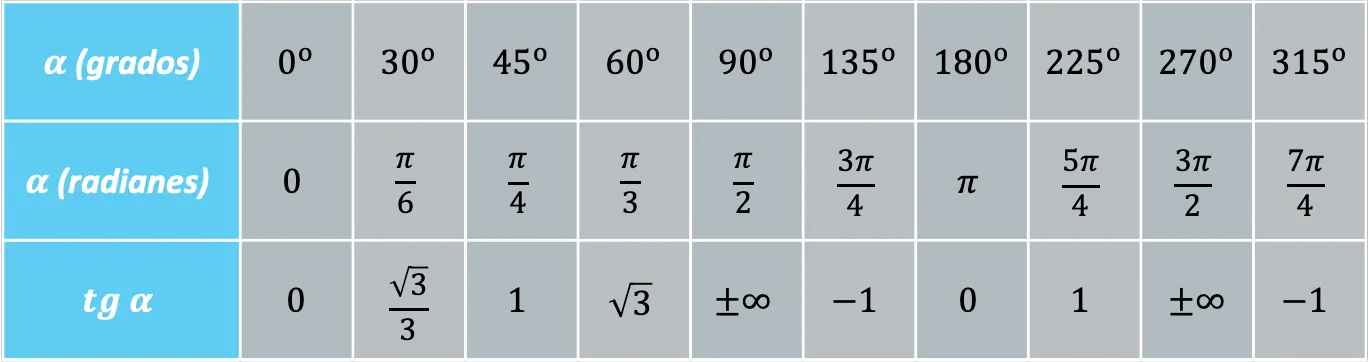
Aan de andere kant kan de raaklijnfunctie worden gekoppeld aan de sinus- en cosinusfuncties door de volgende fundamentele trigonometrische identiteit:
![]()
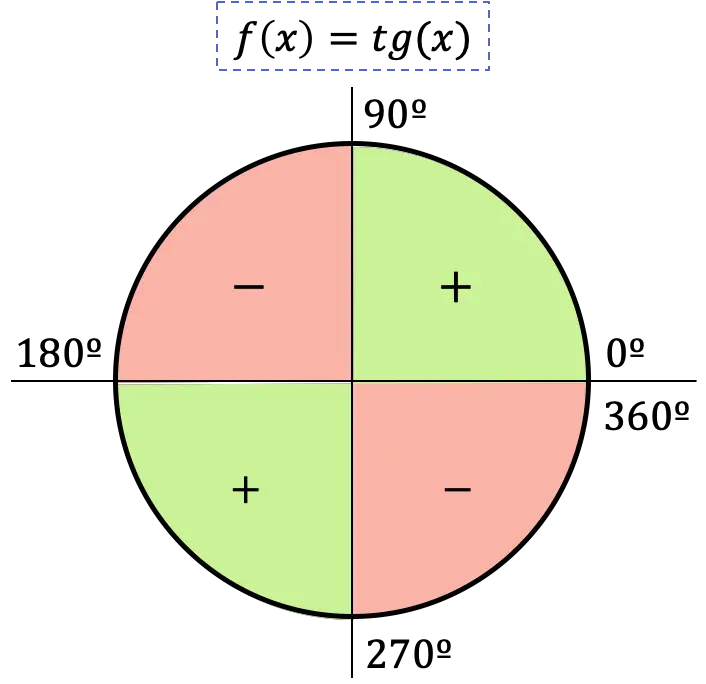
Het teken van de raaklijnfunctie hangt dus af van het kwadrant waarin de hoek zich bevindt:
- Als de hoek tot het eerste kwadrant behoort, zal de raaklijn positief zijn, aangezien in dit kwadrant de sinus en de cosinus ook positief zijn.
- Als de hoek in het tweede kwadrant valt, zal de raaklijn negatief zijn, omdat in dit kwadrant de sinus positief is, maar de cosinus negatief.
- Als de hoek zich in het derde kwadrant bevindt, zal de raaklijn positief zijn, omdat in dit kwadrant de sinus en de cosinus negatief zijn.
- Als de hoek zich in het vierde kwadrant bevindt, zal de raaklijn negatief zijn, aangezien in dit kwadrant de sinus negatief is en in plaats daarvan de cosinus positief.
Grafische weergave van de raaklijnfunctie
Met de waardentabel die we in de vorige sectie hebben gezien, kunnen we de tangensfunctie in een grafiek weergeven. En door de tangensfunctie in een grafiek weer te geven, verkrijgen we:
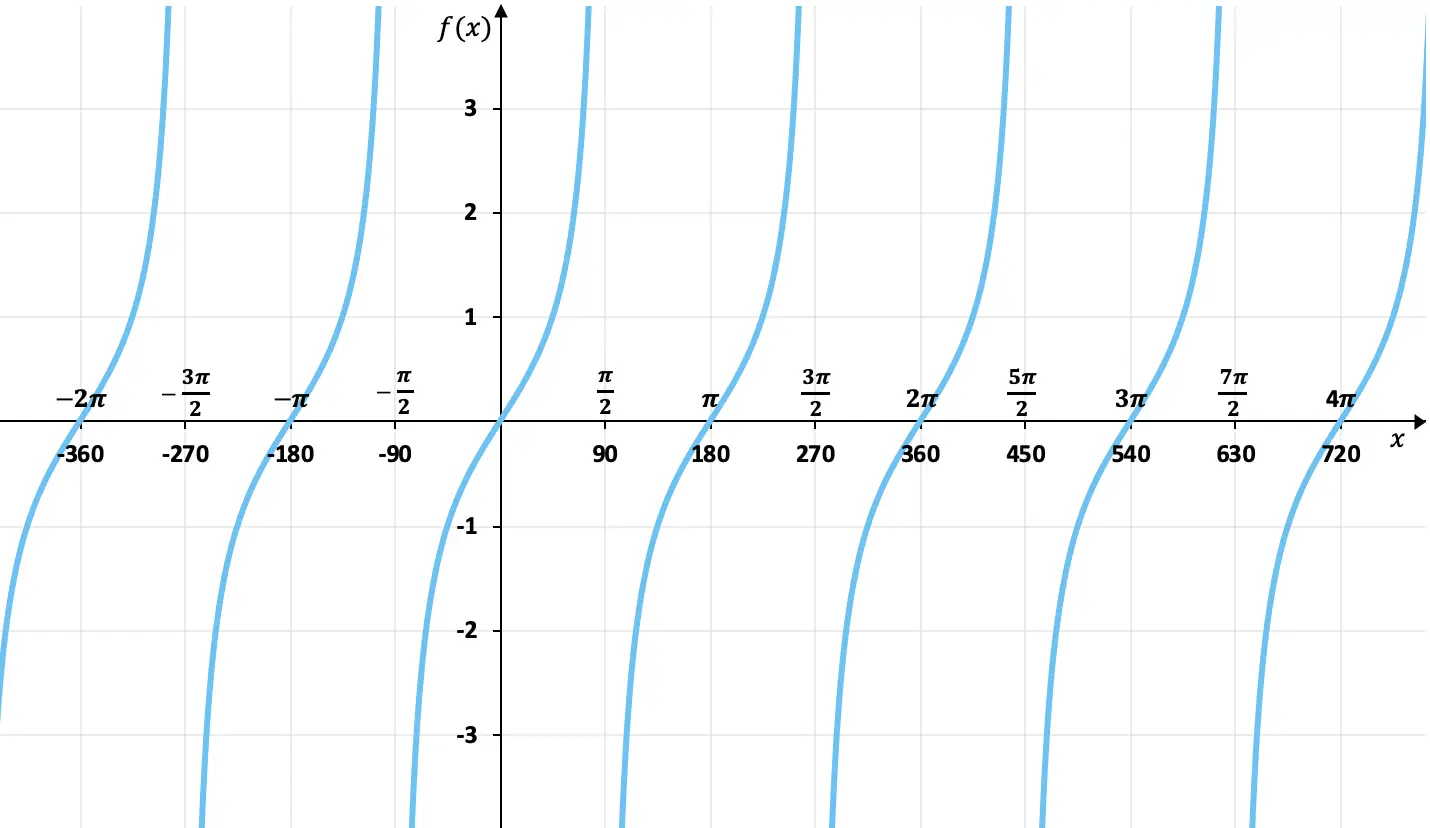
Zoals je in de grafiek kunt zien, zijn de waarden van de afbeeldingen van de raaklijnfunctie niet begrensd, in tegenstelling tot de sinus- en cosinusfuncties. Bovendien worden de waarden elke 180 graden herhaald (π radialen), dus het is een periodieke functie waarvan de periode 180 graden is.
Aan de andere kant kunnen we in deze grafiek zien dat de tangensfunctie oneven is, omdat de tegenovergestelde elementen ervan tegengestelde afbeeldingen hebben, of met andere woorden, hij is symmetrisch ten opzichte van de oorsprong (0,0). De tangens van 45° is bijvoorbeeld 1 waard en die van -45° is -1 waard.
Ten slotte kunnen we ook zien dat de raaklijnfunctie verticale asymptoten heeft. Het komt bijvoorbeeld heel dicht bij de x=90º-lijn, maar raakt deze nooit, en hetzelfde gebeurt elke 180 graden. Dit betekent dat de limiet van de functie op deze punten naar oneindig neigt.
Eigenschappen van de tangensfunctie
De tangensfunctie heeft de volgende kenmerken:
- Het domein van de raaklijnfunctie bestaat uit alle reële getallen, behalve punten waar sprake is van een verticale asymptoot:
![]()
![]()
- Het bereik of bereik van de raaklijnfunctie zijn allemaal reële getallen.
![]()
- Het is een continue en oneven functie met periodiciteit π.
![]()
- Dit type trigonometrische functie heeft één snijpunt met de y-as (Y-as) op het punt (0,0).
![]()
- In plaats daarvan onderschept het periodiek de abscis (X-as) op verschillende coördinaten van pi.
![]()
- De functie is strikt stijgend over het gehele domein en heeft dus geen maximum of minimum.
- De afgeleide van de raaklijn is:
![]()
- Ten slotte is de integraal van de raaklijnfunctie:
![]()
Periode van de tangensfunctie
In tegenstelling tot andere trigonometrische functies zoals sinus en cosinus, heeft de tangensfunctie geen grootte, aangezien deze geen maximale of minimale waarde heeft. Het is echter een periodieke functie, dat wil zeggen dat de waarden ervan worden herhaald met een frequentie zoals we in de grafiek zagen.
![]()
- De periode van de raaklijnfunctie is de afstand tussen twee punten waarop de grafiek wordt herhaald, en wordt berekend met de volgende formule:
![]()
raaklijnstelling
Hoewel de raaklijnformule normaal gesproken wordt gebruikt in rechthoekige driehoeken, is er ook een stelling die op elk type driehoek kan worden toegepast: de raaklijnstelling.
De raaklijnstelling relateert de zijden en hoeken van elke driehoek als volgt:
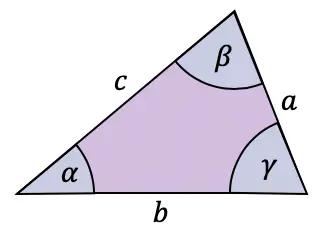
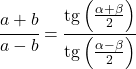
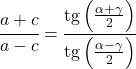
Relaties van de raaklijnfunctie met andere trigonometrische verhoudingen
Hieronder heb je de relaties van de raaklijn met de belangrijkste goniometrische verhoudingen van de trigonometrie.
Relatie met de borst
- De raaklijn en de sinus van een hoek zijn als volgt met elkaar verbonden:
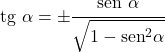
Cosinus verhouding
- Op dezelfde manier zijn de raaklijn en de cosinus van een hoek gerelateerd aan de volgende gelijkheid:
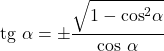
Relatie met de cosecans
- Hoewel het moeilijk te bewijzen is, kan de raaklijn zo worden opgelost dat deze alleen van de cosecans afhangt:
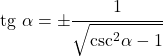
Relatie met de secans
- De raaklijn en de secans van een hoek zijn gerelateerd aan de volgende vergelijking:
![]()
Relatie met de cotangens
- Tangens en cotangens zijn multiplicatieve inverses:
![]()