Symmetrische matrix

Op deze pagina vind je de uitleg van wat symmetrische matrices zijn. Bovendien laten we u zien hoe u snel kunt identificeren wanneer een matrix symmetrisch is, samen met verschillende voorbeelden, zodat u geen twijfels heeft. Je vindt er ook alle eigenschappen van symmetrische matrices. En ten slotte leggen we een specifiek kenmerk uit dat elke vierkante matrix heeft: deze kan worden ontleed in de som van een symmetrische matrix en een antisymmetrische matrix.

Wat is een symmetrische matrix?

De definitie van een symmetrische matrix is als volgt:

Een symmetrische matrix is een vierkante matrix waarvan de transpositie gelijk is aan de matrix zelf.

$A^t = A$

Goud

$A^t$

vertegenwoordigt de getransponeerde matrix van

$A$

Zodra we het concept van een symmetrische matrix kennen, zullen we zien hoe elke symmetrische matrix gemakkelijk kan worden geïdentificeerd:

Wanneer is een matrix symmetrisch?

Het herkennen van de structuur van een symmetrische matrix is heel eenvoudig: het element van rij i en kolom j moet identiek zijn aan het element van rij j en kolom i . En de waarden van de hoofddiagonaal van de matrix kunnen elk zijn.

Voorbeelden van symmetrische matrices

Hier zijn verschillende voorbeelden van symmetrische matrices om u te helpen begrijpen:

Voorbeeld van een symmetrische matrix van orde 2 × 2

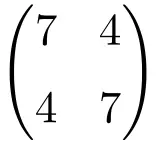
voorbeeld van een symmetrische matrix met afmeting 2x2

Voorbeeld van een symmetrische matrix met afmeting 3×3

voorbeeld van een symmetrische matrix met afmeting 3x3

Voorbeeld van een symmetrische matrix van maat 4×4

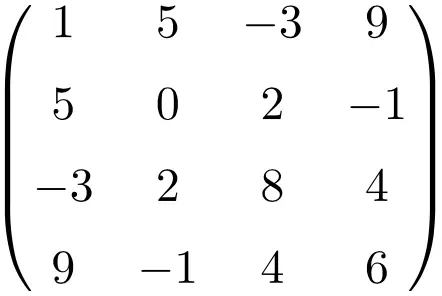
voorbeeld van een symmetrische matrix met afmeting 4x4

Door deze drie matrices te transponeren, verifiëren we dat ze symmetrisch zijn, omdat de getransponeerde matrices equivalent zijn aan hun respectieve originele matrices.

Waarom wordt het een symmetrische matrix genoemd?

Als je goed naar de voorgaande voorbeelden kijkt, is de hoofddiagonaal van een symmetrische matrix een symmetrieas, of met andere woorden, deze fungeert als een spiegel tussen de getallen boven de diagonaal en die eronder. Om deze reden worden dit soort matrices symmetrisch genoemd.

Eigenschappen van symmetrische matrices

De kenmerken van symmetrische matrices zijn als volgt:

Het optellen (of aftrekken) van twee symmetrische matrices levert nog een symmetrische matrix op. Omdat het transponeren van twee opgetelde (of afgetrokken) matrices gelijk staat aan het afzonderlijk transponeren van elke matrix:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Elke symmetrische matrix vermenigvuldigd met een scalair geeft ook aanleiding tot een andere symmetrische matrix.

Op dezelfde manier is het matrixproduct tussen twee symmetrische matrices niet altijd gelijk aan een andere symmetrische matrix, alleen dan en slechts dan als de twee matrices kunnen worden omgezet. Deze voorwaarde kan worden bewezen met de getransponeerde matrixvermenigvuldigingseigenschap:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

De macht van een symmetrische matrix geeft aanleiding tot een andere symmetrische matrix, zolang de exponent een geheel getal is.

Het is duidelijk dat de unitaire matrix en de nulmatrix voorbeelden zijn van symmetrische matrices.

Een matrix die congruent is aan een symmetrische matrix moet ook symmetrisch zijn.

Als een symmetrische matrix regelmatig of inverteerbaar is, dan is de inverse matrix ook symmetrisch.

Hetzelfde geldt voor de adjunct van een symmetrische matrix: de adjunct-matrix van een symmetrische matrix geeft een andere symmetrische matrix als oplossing.

Een echte symmetrische matrix is ook een normale matrix.

Omdat symmetrische matrices een speciaal geval zijn van Hermitische matrices, zijn alle eigenwaarden (of eigenwaarden) van een symmetrische matrix reële getallen.

De spectrale stelling vertelt ons dat alle matrices waarvan de elementen reëel zijn, diagonaliseerbare matrices zijn en bovendien wordt de diagonalisatie uitgevoerd door middel van een orthogonale matrix. Daarom zijn alle echte symmetrische matrices orthogonaal diagonaliseerd.

Aan de andere kant kunnen symmetrische matrices met complexe getallen worden gediagonaliseerd via een unitaire matrix.

De Hessische matrix is altijd symmetrisch.

Ontleding van een vierkante matrix in een symmetrische matrix en een antisymmetrische matrix

Een speciaal kenmerk van vierkante matrices is dat ze kunnen worden ontleed in de som van een symmetrische matrix plus een antisymmetrische matrix.

De formule waarmee we dit kunnen doen is als volgt:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Waar C de vierkante matrix is die we willen ontleden, ^wordt C getransponeerd, en tenslotte zijn S en A respectievelijk de symmetrische en antisymmetrische matrices waarin de matrix C wordt ontleed.

Hieronder heb je een opgeloste oefening om te zien hoe dit wordt gedaan. Laten we de volgende matrix ontleden:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

We berekenen de symmetrische en antisymmetrische matrix met de formules:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

En we kunnen controleren of aan de vergelijking is voldaan door de twee matrices op te tellen:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅