Op deze pagina vindt u de uitleg hoe het optellen van polynomen in zijn werk gaat. Bovendien kunt u voorbeelden zien van sommen van polynomen en zelfs oefeningen die stap voor stap worden opgelost. Tenslotte leggen we ook uit wat de eigenschappen zijn van dit soort bewerkingen met polynomen.
Hoe polynomen toevoegen?
Om in de wiskunde twee of meer polynomen op te tellen, moeten de termen van de polynomen die vergelijkbaar zijn bij elkaar worden opgeteld. Dat wil zeggen dat het optellen van polynomen bestaat uit het optellen van termen die hetzelfde letterlijke deel hebben (dezelfde variabelen en dezelfde exponenten).
Een som van polynomen kan dus op twee verschillende manieren worden gedaan: met de verticale methode of met de horizontale methode. Hieronder vindt u de uitleg van beide procedures, maar we raden u aan eerst te leren hoe u polynomen verticaal optelt en vervolgens overgaat naar de horizontale methode. Blijf uiteraard bij degene die u verkiest.
Verticale polynomen toevoegen
Vervolgens zullen we zien hoe twee polynomen verticaal worden opgeteld aan de hand van een voorbeeld:
- Voeg de volgende twee polynomen toe:
![]()
![]()
Het eerste dat we moeten doen is de ene polynoom onder de andere plaatsen, zodat de soortgelijke termen van de twee polynomen in kolommen worden uitgelijnd:
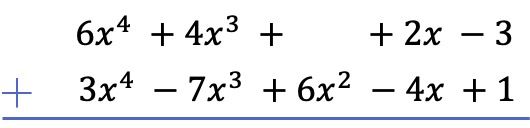
Waarschuwing: Als een polynoom geen term van een bepaalde graad heeft, moet de ruimte leeg worden gelaten. Bijvoorbeeld
![]()
U beschikt niet over een monomial van graad 2, daarom is er een lege ruimte op uw site.
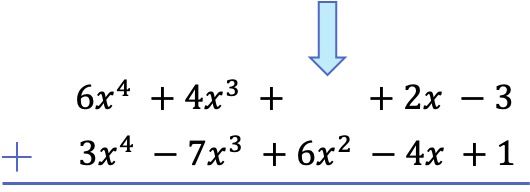
Nadat we alle termen van de hoogste graad naar de laagste graad hebben geordend, voegen we de coëfficiënten in elke kolom toe, waarbij de letterlijke delen gelijk blijven:
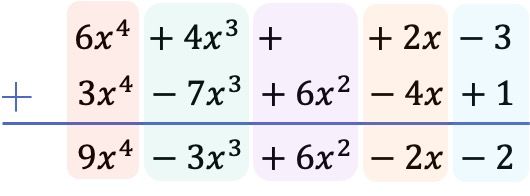
Het resultaat verkregen uit de som van de 2 polynomen is dus:
![]()
Nu je de optelling van polynomen begrijpt, weet je dat je ook breuken kunt optellen die uit polynomen bestaan. Dit type bewerking wordt algebraïsche breukoptelling genoemd. Klik op deze link en leer niet alleen hoe de sommen van algebraïsche breuken worden berekend, maar ook hoe alle bewerkingen met algebraïsche breuken worden opgelost.
Horizontale toevoeging van polynomen
We hebben zojuist gezien hoe je polynomen verticaal kunt optellen, maar nu gaan we kijken naar de andere methode voor het optellen van polynomen: horizontaal optellen van polynomen. Deze procedure is zeker sneller dan de vorige, maar het is noodzakelijk om de concepten van polynomen beter te beheersen.
Laten we aan de hand van een voorbeeld eens kijken waaruit deze methode voor het optellen van polynomen bestaat. En zodat je de verschillen tussen de twee methoden kunt zien, voegen we dezelfde polynomen toe als in het vorige voorbeeld:
- Bereken de som van de volgende twee polynomen:
![]()
![]()
Je moet eerst de twee polynomen in dezelfde bewerking positioneren, dat wil zeggen de een na de ander:
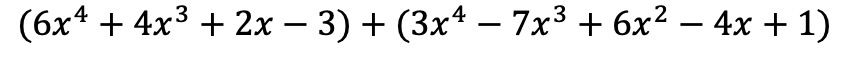
En nu voegen we de termen toe die identieke letterlijke delen hebben, dat wil zeggen de termen met dezelfde variabelen (letters) en dezelfde exponenten. Termen die niet vergelijkbaar zijn, kunnen niet worden toegevoegd.
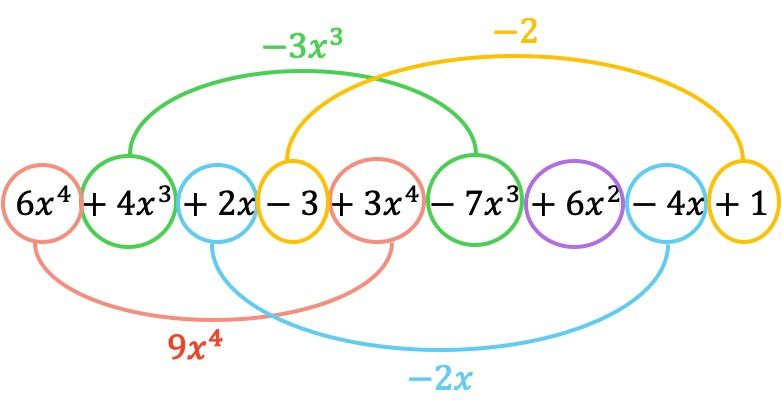
De polynoom die voortvloeit uit de optelling is daarom:

Zoals u kunt zien, kregen we met beide methoden hetzelfde resultaat, dus bij het optellen van polynomen kunt u de methode gebruiken die het beste bij u past.
Problemen met het optellen van polynomen opgelost
Zodat je kunt oefenen, laten we je een aantal opgeloste oefeningen van sommen van veeltermen achter. Als u vragen heeft, kunt u deze stellen in de opmerkingen op de pagina en wij zullen deze zo snel mogelijk beantwoorden.
Oefening 1
Voeg de volgende twee polynomen toe:
![]()
![]()
In dit geval tellen we de twee polynomen verticaal op. Om dit te doen, ordenen we de polynomen op graad en voegen we de monomialen toe die zich in dezelfde kolom bevinden:
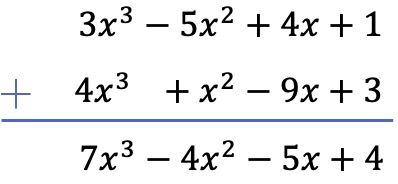
Oefening 2
Los de som op van de volgende twee polynomen:
![]()
![]()
We zullen de twee polynomen optellen met behulp van de verticale methode. We ordenen daarom de polynomen op graad en voegen de termen toe die zich in dezelfde kolom bevinden:
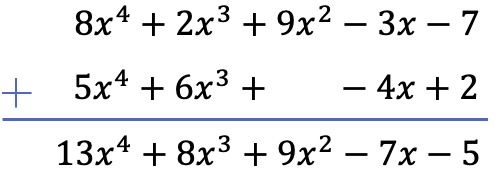
Merk op dat in dit specifieke geval een lege ruimte moet worden gelaten in de kolom van graad 2 van de tweede polynoom, omdat deze geen kwadratische term heeft.
Oefening 3
Wat is de som van de volgende twee polynomen?
![]()
![]()
We zullen de optelling van de twee polynomen uitvoeren met behulp van de verticale methode. DUS:
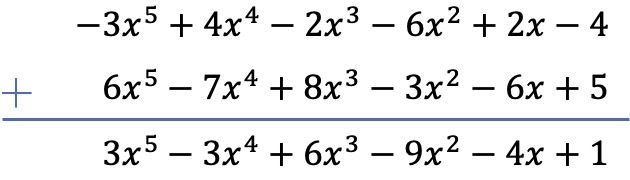
Oefening 4
Bereken de som van de volgende drie polynomen:
![]()
![]()
![]()
We zullen de som van de 3 polynomen berekenen met behulp van de verticale methode. We plaatsen daarom de polynomen geordend op graad en voegen de termen toe die zich in dezelfde kolom bevinden:
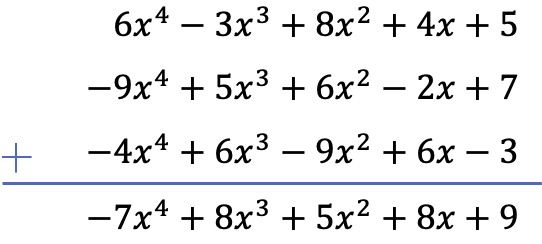
👉👉👉Nu je hebt gezien hoe twee polynomen optellen, ben je misschien geïnteresseerd in een andere karakteristieke bewerking van polynomen: de gemeenschappelijke factor. Het extraheren van een gemeenschappelijke factor uit een polynoom is behoorlijk ingewikkeld (en moeilijk te begrijpen). Daarbij worden zelfs veel fouten gemaakt. Daarom hebben we een handleiding opgesteld waarin we stap voor stap uitleggen hoe u de gemeenschappelijke factor kunt extraheren , zodat u deze perfect begrijpt en geen fouten maakt bij het uitvoeren van deze handeling. Ontdek wat de tips zijn voor het extraheren van de gemeenschappelijke factor uit een polynoom door op de link te klikken.
Eigenschappen van het toevoegen van polynomen
De som van polynomen heeft de volgende kenmerken:
- Associatieve eigenschap : Bij het optellen van 3 of meer polynomen maakt het niet uit hoe de polynomen gegroepeerd zijn, omdat het resultaat altijd hetzelfde is. Dat wil zeggen, de volgende gelijkheid wordt geverifieerd:
![]()
- Commutatieve eigenschap : bij de optelling van polynomen verandert de volgorde van de optellingen het resultaat van de optelling niet.
![]()
- Neutraal element : Het is duidelijk dat het optellen van een polynoom plus een ander polynoom met een numerieke waarde nul gelijk is aan het eerste polynoom.
![]()
- Tegenoverliggend element : Het resultaat van het optellen van een polynoom plus zijn tegengestelde polynoom is altijd nul.
![]()
Wat vind jij van de uitleg? Vond je dit nuttig? Welke methode voor het optellen van polynomen heeft uw voorkeur, verticaal of horizontaal? We lezen je in de reacties! 👀