▷ Schuine asymptoot van een functie (opgeloste oefeningen)

In dit artikel leggen we uit wat de schuine asymptoten van een functie zijn. Je leert wanneer een functie een schuine asymptoot heeft en hoe deze wordt berekend. En bovendien kun je voorbeelden van schuine asymptoten zien en oefenen met oefeningen die stap voor stap worden opgelost.

Wat is een schuine asymptoot?

De schuine asymptoot van een functie is een hellende lijn die de grafiek voor onbepaalde tijd nadert zonder deze ooit te overschrijden. Bijgevolg zijn alle schuine asymptoten lijnen met de vergelijking y=mx+n .

De helling en oorsprong van een schuine asymptoot worden berekend met behulp van de volgende formules:

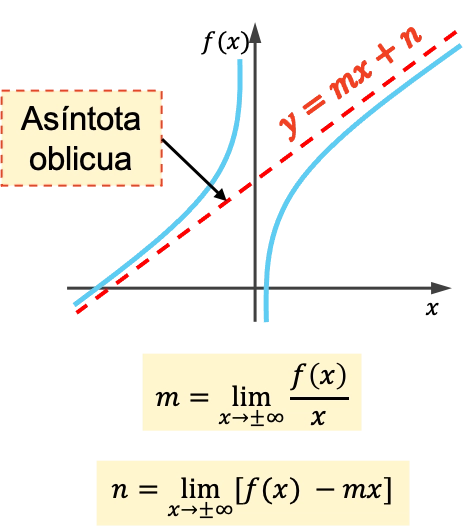
Hoe de schuine asymptoot van een functie te berekenen

Om de schuine asymptoot van een functie te berekenen, moeten de volgende stappen worden uitgevoerd:

Bereken de limiet tot oneindig van de functie gedeeld door x.
Als de bovenstaande limiet resulteert in een reëel getal dat niet nul is, betekent dit dat de functie een schuine asymptoot heeft. En bovendien zal de helling van de schuine asymptoot de waarde zijn die bij de limiet wordt verkregen.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

In dit geval hoeft u alleen nog maar het snijpunt van de schuine asymptoot te berekenen door de volgende limiet op te lossen:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Let op: de limieten moeten worden berekend op plus en min oneindig, maar normaal gesproken geven ze hetzelfde resultaat en daarom vereenvoudigen we door ±∞ te plaatsen. Maar als de grenzen bij plus en min oneindig verschillend waren, zouden de linker schuine asymptoot en de rechter schuine asymptoot afzonderlijk moeten worden berekend.

Schuin asymptootvoorbeeld

Vervolgens nemen we de schuine asymptoot van de volgende rationale functie, zodat u een voorbeeld kunt zien van hoe dit wordt gedaan:

$f(x)=\cfrac{x^2+1}{x}$

De schuine asymptoten zijn van het type

$y=mx+n.$

We berekenen dus eerst de helling van de lijn

$m$

met de bijbehorende formule:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

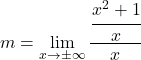
Om deze limiet op te lossen moeten we de eigenschappen van breuken toepassen:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

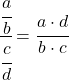
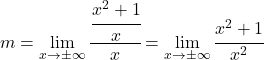
En nu berekenen we de limiet:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

In dit geval is het resultaat van de onbepaaldheid van oneindigheid tussen oneindigheid de verdeling van de coëfficiënten van x van de hoogste graad, aangezien de teller en de noemer van dezelfde orde zijn.

De bovenstaande limiet geeft een reëel getal dat niet nul is, dus de functie heeft een schuine asymptoot. We zullen nu het y-snijpunt berekenen

$n$

van de asymptoot met behulp van de overeenkomstige formule:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

We proberen de limiet te berekenen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Maar we krijgen onbepaaldheid oneindig min oneindig. Het is daarom noodzakelijk om de termen terug te brengen tot een gemeenschappelijke noemer. Om dit te doen, vermenigvuldigen en delen we de x door de noemer van de breuk:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Nu de twee termen dezelfde noemer hebben, kunnen we ze groeperen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

We werken met de teller:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

En ten slotte lossen we de limiet op:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Dus n =0. Daarom is de schuine asymptoot een lineaire functie:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

De bestudeerde functie wordt weergegeven in de onderstaande grafiek. Zoals je kunt zien, komt de functie heel dicht bij de lijn y=x, maar raakt deze nooit, omdat deze een schuine asymptoot is:

Opgeloste oefeningen op schuine asymptoten

Oefening 1

Zoek de schuine asymptoot van de volgende rationale functie:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Zie de oplossing

De schuine asymptoten hebben de vorm

$y=mx+n$

is het daarom noodzakelijk om de parameters m en n te berekenen. We berekenen eerst m door de formule toe te passen:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

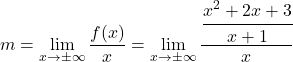
We vereenvoudigen de breuk door de eigenschappen van breuken toe te passen:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

En we lossen de limiet op:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Dus m =1. Laten we nu het snijpunt van de schuine asymptoot berekenen door de formule ervan toe te passen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

We proberen de limiet te berekenen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Maar we krijgen de onbepaalde vorm oneindig min oneindig. We moeten daarom de termen terugbrengen tot een gemeenschappelijke noemer en ze vervolgens groeperen:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

En ten slotte lossen we de limiet op:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

Kortom, de schuine asymptoot van de functie is:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Oefening 2

Vind alle schuine asymptoten van de volgende rationale functie:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Zie de oplossing

Eerst gebruiken we de formule voor de helling van de schuine asymptoot:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

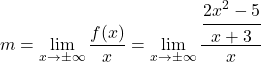
We vereenvoudigen de breuk door de eigenschappen van breuken toe te passen:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

En we bepalen de limiet:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

De limiet geeft een ander reëel getal dan nul, dus het is een rationale functie met een schuine asymptoot waarvan de helling 2 is.

Laten we nu het snijpunt berekenen door de overeenkomstige formule toe te passen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

We proberen de limiet te berekenen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Maar we verkrijgen het verschil-onbepaaldheid van oneindigheden. Daarom reduceren we de termen tot een gemeenschappelijke noemer en gaan we als volgt te werk:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

En ten slotte lossen we de limiet op:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

Samenvattend is de schuine asymptoot van de fractionele functie:

$y = mx+n$

$\bm{y=2x-6}$

Wat is een schuine asymptoot?

Hoe de schuine asymptoot van een functie te berekenen

Schuin asymptootvoorbeeld

Opgeloste oefeningen op schuine asymptoten

Oefening 1

Oefening 2

Laat een reactie achter Reactie annuleren