De regel van Ruffini is een wiskundige procedure , ontwikkeld door Paolo Ruffini , waarmee we polynomen van de vorm (x – a) kunnen verdelen. Deze wiskundige methode wordt ook wel synthetische deling genoemd. Maar hoe wordt deze procedure gebruikt en wat zijn de stappen? En hoe los je een Ruffini-oefening op met de rekenmachine? We zullen je dit alles op een samengevatte en gemakkelijk te begrijpen manier in dit artikel uitleggen, daarnaast zullen we de beste rekenmachines voor Ruffini aanbevelen.
Ruffini-calculator online
Als u een polynoom wilt ontbinden in factoren, kunt u deze rekenmachine gebruiken, waarmee u elke uitdrukking kunt ontbinden, zolang u deze maar schrijft met de volgende symbolen: ^ (verhogen) en / (delen). En u kunt gerust zijn, want deze rekenmachine kan polynomen van graad 3 en zelfs hogere graden ontbinden. Het is daarom de ultieme rekentool voor het online ontbinden van polynomen.
Hoe Ruffini aanbrengen?
In deze sectie leggen we uit hoe je Ruffini uitvoert en lossen we een specifiek voorbeeld op met behulp van de methode. Op deze manier kun je de hele procedure duidelijk en grafisch zien. Hierdoor kun je dit concept bij de wortel begrijpen en later tijdens het examen onthouden. Daarnaast hebben we een verklarende video toegevoegd waarmee u dit concept kunt begrijpen, zelfs als u twijfels heeft over de schriftelijke uitleg.
Vereisten voor het gebruik van de Ruffini-methode
Voordat u begint met het oplossen van een deling van polynomen of voordat u een polynoom ontbindt in factoren , moet u naar de deler kijken. Als het de eerste graad is, kunnen we doorgaan met de Ruffini-methode. Aan de andere kant, als de deler een graad groter dan 1 heeft, kunnen we de berekening niet oplossen door deze procedure te volgen. Daarom moeten we een andere methode gebruiken om polynomen te delen. Dit is een factor die moet worden gecontroleerd voordat u met de berekeningen begint, omdat u anders veel tijd kunt verliezen.
Procedure voor het delen van polynomen met behulp van de regel van Ruffini
Nu we weten wanneer dit wiskundige hulpmiddel kan worden gebruikt, zullen we zien welke verschillende stappen we moeten volgen om een polynoom te kunnen ontbinden in factoren. Dus vanuit het voorbeeld (x³+3x²-1) / (x-2) moeten we eerst de dividendcoëfficiënten op een horizontale lijn schrijven , waarbij de ontbrekende termen met een nul worden weergegeven. En dan plaatsen we de onafhankelijke term van de deler in het afzonderlijke tegengestelde teken, zoals weergegeven in de afbeelding.
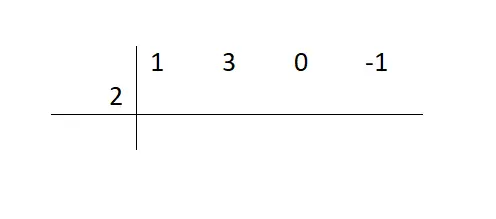
Vervolgens moeten we de eerste coëfficiënt verlagen (de coëfficiënt die gepaard gaat met de variabele die naar een hogere exponent is verhoogd). We zullen niets met dit aantal doen, omdat we het zullen verminderen en doorgaan naar de volgende stap.
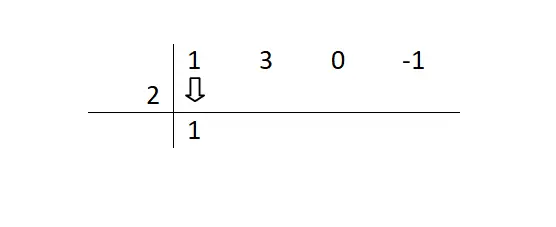
Vervolgens beginnen we met een reeks tamelijk repetitieve stappen: we vermenigvuldigen het getal dat we hebben verlaagd met de deler en plaatsen het resultaat onder de volgende term. Vervolgens voegen we de volgende term toe tussen dit resultaat en schrijven deze naast het eerste getal dat we hebben opgeschreven.
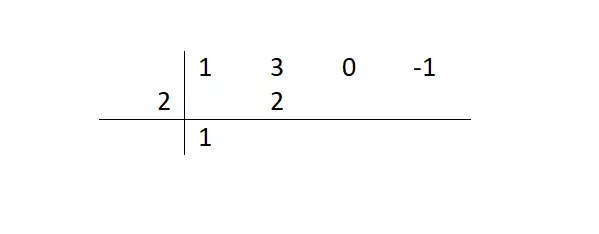
Als we deze reeks stappen volgen totdat we de tabel hebben voltooid, krijgen we de volgende lay-out. Op deze manier weten we dat de rest gelijk is aan 19 (laatste getal dat we hebben berekend) en dat de restuitdrukking (quotiënt) x²+5x+10 zal zijn. Al deze informatie hebben we verkregen uit de cijfers in de onderste rij . En als we een polynoom ontbinden in factoren, moeten we dit quotiënt gebruiken om door te gaan met het vinden van de andere wortels.
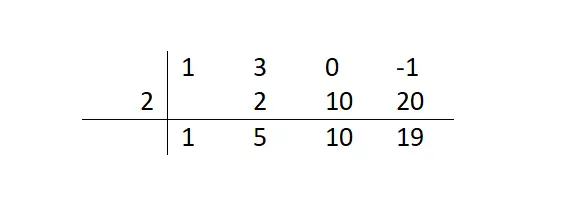
Hoe zet je Ruffini in de rekenmachine?
Om polynomen met Ruffini op de rekenmachine te kunnen delen , hoeft u alleen maar naar de oplossers van de rekenmachine te gaan, dat wil zeggen naar de modus voor het berekenen van vergelijkingen. En eenmaal binnen selecteren we de optie polynoomvergelijkingen, omdat we een polynoom in factoren willen ontbinden. Vervolgens selecteren we de mate van de uitdrukking en kunnen we de wiskundige editor openen, daarom introduceren we de uitdrukking. Dus als we de wortels van de polynoom hebben, hoeven we deze alleen maar in de vorm (x – a) te schrijven. Deze hele procedure (behalve het wortelgedeelte) is identiek aan degene die we zullen gebruiken om de vergelijkingen met de rekenmachine op te lossen .
De beste rekenmachines voor het berekenen van de stelling van Ruffini
Momenteel zijn er veel rekenmachines die bewerkingen met polynomen kunnen oplossen en deze in factoren kunnen ontbinden. Er zijn echter enkele modellen die eruit springen qua gebruiksgemak en prijs . Twee goede voorbeelden zijn de Casio FX-991SPX II en de Casio FX-991ES PLUS , sterker nog, de uitleg die we in de vorige sectie hebben gegeven is gebaseerd op de werking van deze twee modellen. Hoewel je, zoals we al hebben gezegd, andere wetenschappelijke rekenmachines kunt vinden die je ook zullen helpen Ruffini perfect uit te voeren.
Ruffini-voorbeelden en oefeningen
De regel van Ruffini kan in praktijk worden gebracht door twee polynomen willekeurig te nemen, zolang ze maar de regels volgen die we in het begin hebben besproken. Hoewel je via deze wiskundige procedure ook polynomen met een graad groter dan één kunt ontbinden. Je gaat dus hetzelfde wiskundige mechanisme doornemen en op zijn beurt het concept van de wortel van een polynoom. Vervolgens laten we u twee polynomen zien die u moet ontbinden en een vrij eenvoudige deling, die u moet oplossen met behulp van de methode van Ruffini.
Oefening 1
Ontbind de polynoom in factoren: 2x³-7x²+8x-3
Wortels: x=1 en x=1, we houden dus (x-1)²(2x-3) over
Oefening 2
Ontbind de polynoom in factoren: x³+2x²-x-2
Wortels: x=-2, x=-1 en x=1, dus we houden (x+2)(x+1)(x-1) over
Oefening 3
Los de volgende verdeling tussen polynomen op: (3x³-5x²+2) / (x-2)
Quotiënt: 3x²+x+2, rest: 6
Als je meer Ruffini-oefeningen wilt, raden we je aan dit Superprof-artikel te bekijken, waarin dezelfde procedures worden uitgelegd als in dit artikel. Maar met voorbeelden en oefeningen die enigszins verschillen van die van Ruffini, kun je met meer oefening misschien enkele twijfels oplossen. Hoe dan ook, we hopen dat je onze inhoud en de Ruffini-calculator nuttig vond.