▷ Reststelling: wat het is, voorbeelden en opgeloste oefeningen ✅

Hier vindt u de uitleg van wat de reststelling (of reststelling) is en hoe deze wordt toegepast op polynomen. Ook krijg je voorbeelden te zien en daarnaast te oefenen met stap voor stap opgeloste oefeningen op de reststelling.

Wat is de reststelling?

In de wiskunde zegt de reststelling dat de rest van de deling van een polynoom P(x) door een ander polynoom van de vorm (xa) gelijk is aan de numerieke waarde van het polynoom P(x) voor de waarde x=a. met andere woorden, de rest van de deling P(x):(xa) is equivalent aan P(a).

Voorbeeld van de reststelling

Als we eenmaal hebben gezien wat de reststelling is, gaan we kijken naar een praktisch voorbeeld van de toepassing ervan:

Bereken de rest van de verdeling tussen de volgende twee polynomen:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Om de rest (of residu) van de polynoomdeling te vinden, kunnen we profiteren van de reststelling, omdat in dit geval de delende polynoom de vorm (xa) heeft, dat wil zeggen van de eerste graad is, de coëfficiënt van de variabele x is 1 en heeft een onafhankelijke term.

We passen dus de reststelling toe, die zegt dat de rest van een deling als deze gelijk is aan de numerieke waarde van het dividendpolynoom, geëvalueerd in de onafhankelijke term van het teken-veranderde delerpolynoom, dat wil zeggen P (1).

Om de rest van de deling te vinden, moeten we daarom de polynoom op x = 1 evalueren:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

De rest van de verdeling tussen de polynomen is dus 2 .

Aan de andere kant kunnen we ook met de regel van Ruffini voor delende polynomen controleren of de rest samenvalt met het gevonden resultaat:

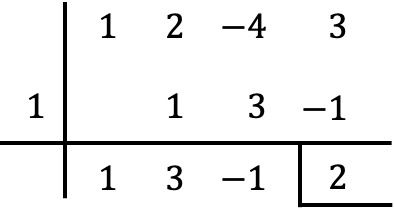
Zoals je kunt zien, is het veel sneller en gemakkelijker om de rest van een deling van een polynoom door een binomiaal te bepalen met de reststelling dan met de regel van Ruffini, omdat er veel minder berekeningen worden uitgevoerd.

Rest- en factorstelling

Uit de reststelling en de definitie van de wortel (of nul) van een polynoom kunnen we de factorstelling afleiden. De factorstelling impliceert dus het volgende:

De factorstelling zegt dat een polynoom P(x) deelbaar is door een andere polynoom van de vorm (xa) als en slechts als P(a)=0. En in dit geval betekent dat dat a een wortel of nul is van de polynoom P(x).

Bovendien betekent dit volgens de reststelling dat als een polynoom deelbaar is door een andere polynoom, de rest van de deling nul is, aangezien P(a) = 0.

Als we bijvoorbeeld een bepaald polynoom hebben:

$P(x)=x^2+2x-8$

Dit polynoom is deelbaar door de binominale (x-2) omdat P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Omdat x=2 de polynoom P(x) opheft, betekent dit dat x=2 een wortel is van genoemde polynoom.

En verder, aangezien P(2)=0, kunnen we dankzij de reststelling weten dat de rest van de deling

$\cfrac{x^2+2x-8}{x-2}$

is gelijk aan 0.

Opgeloste oefeningen van de reststelling

Om het begrip van de reststelling af te ronden, hebben we een aantal oefeningen voorbereid die stap voor stap zijn opgelost, zodat u kunt oefenen. Wij adviseren je om de oefening eerst zelf te proberen en daarna te controleren of je het goed hebt gedaan.

Oefening 1

Vind, met behulp van de reststelling, de rest van de polynomiale deling

$\cfrac{P(x)}{Q(x)}$

, zijnde de polynomen die bij de bewerking betrokken zijn:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Zie de oplossing

Het delerpolynoom bestaat alleen uit een term van de eerste graad en een onafhankelijke term, en bovendien is de coëfficiënt van de term van de eerste graad 1. We kunnen daarom de reststelling gebruiken.

En om de reststelling toe te passen, volstaat het om het dividendpolynoom te evalueren in de onafhankelijke term van het delerpolynoom met veranderd teken, of met andere woorden: we moeten P(2) berekenen.

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

De rest van de verdeling tussen de twee polynomen is dus 21 .

Oefening 2

Gegeven de polynoom

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Vind de verkregen rest door deze te delen door elk van de volgende polynomen:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Zie de oplossing

Omdat alle delende polynomen voldoen aan de voorwaarden van de reststelling, kunnen we deze stelling gebruiken om de rest van elke deling te bepalen:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Oefening 3

Bereken hoeveel de parameter waard moet zijn

$m$

zodat de rest van de verdeling van polynomen

$\cfrac{P(x)}{Q(x)}$

gelijk zijn aan 3, beide zijn polynomen:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Zie de oplossing

In dit specifieke geval bestaat de delende polynoom uit een monomiaal van de eerste graad en een onafhankelijke term, en bovendien is de coëfficiënt van de monomiaal van de eerste graad 1. We kunnen daarom de reststelling gebruiken.

En om de reststelling te gebruiken, vervangt u eenvoudigweg de onafhankelijke term van de delende polynoom door een verandering van teken waarbij er in de verdeelde polynoom een x staat, we moeten daarom P(-3) oplossen.

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Maar uiteraard verkrijgen we een resultaat gebaseerd op het onbekende

$m.$

De probleemstelling vertelt ons echter dat de rest gelijk moet zijn aan drie, dus moeten we de gevonden rest gelijk stellen aan 3:

$3m-63 = 3$

En tenslotte lossen we de vergelijking op:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Oefening 4

Bepaal met de factor- en reststelling of het polynoom is

$P(x)$

deelbaar is door de polynoom

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Zie de oplossing

Dus dat is de polynoom

$P(x)$

deelbaar zijn door de polynoom

$Q(x)$

de verdeling tussen deze twee polynomen moet exact zijn en daarom moet de rest nul zijn.

Dan, aangezien het delerpolynoom is

$(x+2),$

Door de factorstelling en de reststelling weten we dat de polynoom

$P(x)$

deelbaar zal zijn door de polynoom

$Q(x)$

als deze gevuld is

$P(-2)=0.$

We moeten daarom kijken of deze gelijkheid wordt geverifieerd:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

De rest van de divisie inderdaad

$\cfrac{P(x)}{Q(x)}$

is gelijk aan 0, dus de polynoom

$P(x)$

Ja, het is deelbaar door de andere polynoom

$Q(x).$

Wat vind jij van de uitleg? Vond je het leuk? Laten we hopen! Vergeet niet dat u uw suggesties of vragen in de reacties kunt achterlaten. ⬇⬇⬇ We lezen jullie allemaal! 😁😁

Rest (of residu) stelling

Wat is de reststelling?

Voorbeeld van de reststelling

Rest- en factorstelling

Opgeloste oefeningen van de reststelling

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren