Relatieve posities van een lijn en een vlak

Op deze pagina vindt u de relatieve posities van een lijn en een vlak. We leggen je uit hoe de relatieve positie tussen een lijn en een vlak wordt berekend (2 methoden) en bovendien kun je stap voor stap voorbeelden en oefeningen zien die zijn opgelost.

Wat zijn de relatieve posities tussen een lijn en een vlak?

Voordat we naar alle mogelijke relatieve posities tussen een lijn en een vlak kijken, moeten we uiteraard weten wat lijnen zijn en wat een vlak is . Dus als u deze twee concepten nog steeds niet helemaal duidelijk heeft, raden wij u aan eerst een kijkje te nemen op de gelinkte pagina’s waar het in detail wordt uitgelegd.

In de analytische meetkunde zijn er dus slechts drie relatieve posities in de ruimte tussen een lijn en een vlak:

Lijn in het vlak : wanneer de lijn in het vlak ligt, betekent dit dat ze een oneindig aantal punten gemeen hebben.
Parallelle lijn en vlak : Een lijn en een vlak zijn evenwijdig als ze geen gemeenschappelijk punt hebben.
Snijlijn en vlak : Een lijn en een vlak snijden elkaar wanneer de lijn het vlak op een punt snijdt. Ze hebben dus maar één ding gemeen.

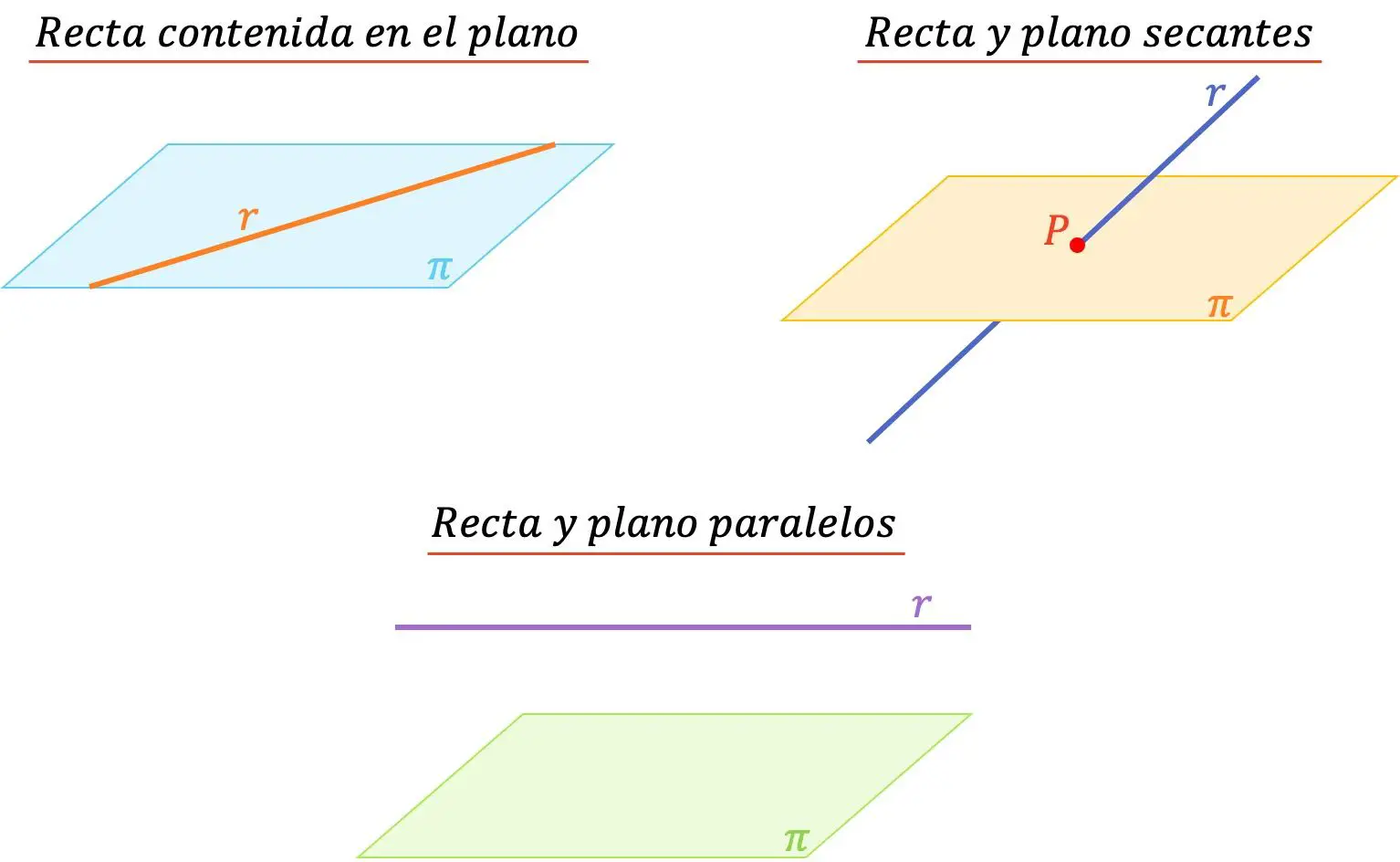
Aan de andere kant, wanneer de lijn zich in het vlak bevindt of wanneer ze evenwijdig aan elkaar zijn, zal de hoek die ze vormen 0° zijn. Aan de andere kant, wanneer de lijn en het vlak elkaar snijden, kan de hoek tussen de twee geometrische elementen variëren van 0° (niet inbegrepen) tot 90° (inclusief).

Hoe bereken je de relatieve positie van een lijn en een vlak?

Er zijn hoofdzakelijk twee methoden om de relatieve positie tussen een lijn en een vlak in de ruimte te vinden: door middel van bereiken of door vectoren .

Wanneer de lijn wordt uitgedrukt als een impliciete (of algemene) vergelijking, is het gemakkelijker om de rangschikkingsmethode te gebruiken. Aan de andere kant, als de lijn wordt gegeven met een ander type vergelijking, bijvoorbeeld als deze de vorm heeft van een vector-, parametrische of continue vergelijking, is het sneller om de vectormethode te gebruiken.

Als u niet meer weet hoe de vergelijkingen van de lijn eruit zien, laten we een pagina achter waarop u alle vergelijkingen van de lijn kunt raadplegen. Hier vind je alle vergelijkingen van de lijn, een formule om snel de vergelijking te vinden van een lijn die door twee punten gaat, voorbeelden en oefeningen die stap voor stap worden opgelost.

Daarom is het praktischer om afhankelijk van het probleem de ene of de andere methode te gebruiken. Om deze reden raden we u aan te weten hoe u beide procedures moet uitvoeren. Hieronder vindt u de uitleg van beide methoden met voorbeelden.

Wanneer de lijn de vorm heeft van een impliciete (of algemene) vergelijking

Eén manier om de relatieve positie tussen een lijn en een vlak te bepalen, is door de rangorde van twee matrices te berekenen.

Als de lijn wordt gedefinieerd door zijn impliciete (of algemene) vergelijkingen:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

En het plan wordt ook uitgedrukt in de vorm van een algemene vergelijking:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

We zullen A de matrix noemen die is samengesteld uit de coëfficiënten A, B en C van de vergelijkingen van het vlak en de lijn:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

En de matrix A’ zal de uitgebreide matrix zijn met alle coëfficiënten van de twee vergelijkingen:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Vervolgens wordt de relatieve positie tussen de lijn en het vlak bepaald door de waarde van de omvang van de twee voorgaande matrices volgens de volgende tabel:

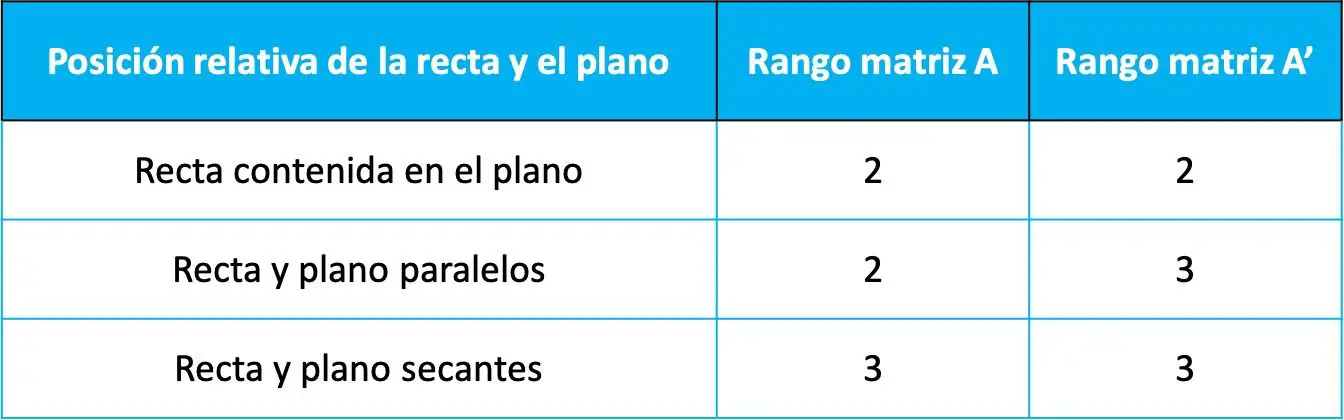
bestudeer de relatieve positie tussen een lijn en een vlak in de ruimte in afstanden

Dat de relatieve posities afhangen van de rangorde van deze twee matrices kan worden aangetoond uit de Rouche-Frobenius toerem (een stelling die wordt gebruikt om stelsels van lineaire vergelijkingen op te lossen). Op deze pagina gaan we de demonstratie echter niet doen omdat het niet nodig is om het te weten en het ook niet veel oplevert.

Voorbeeld van hoe u de relatieve positie van een lijn en een vlak kunt vinden op basis van bereiken

Zodat je precies kunt zien hoe dit moet, lossen we als voorbeeld een oefening op:

Bestudeer de relatieve positie tussen de volgende lijn en het volgende vlak:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

De lijn wordt gedefinieerd door twee elkaar snijdende vlakken, dat wil zeggen dat deze wordt uitgedrukt als een impliciete vergelijking. Daarom zullen we de rangschikkingsmethode gebruiken om de relatieve positie tussen de lijn en het vlak te bestuderen.

Het eerste wat je moet doen is de matrix A en de uitgebreide matrix A’ construeren met de coëfficiënten van de vergelijkingen:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

En nu moeten we de rangorde van elke matrix berekenen. We vinden eerst de omvang van de matrix A aan de hand van determinanten:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

De determinant van matrix A is nul, maar bevat een 2×2-submatrix waarvan de determinant verschilt van nul, dus het is een matrix van rang 2.

Aan de andere kant is het ook noodzakelijk om de rangorde van de matrix A’ te berekenen. En het bereik van de uitgebreide matrix A’ zal altijd minstens hetzelfde zijn als dat van matrix A, dus we hoeven alleen maar te controleren of deze van rang 3 of 2 is:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Aan de andere kant heeft de uitgebreide matrix A’ wel een 3×3-subdeterminant die verschilt van 0, en is daarom van rang 3.

Dus omdat matrix A van rang 2 is en matrix A’ van rang 3 is, zijn de lijn en het vlak evenwijdig .

Wanneer de lijn de vorm heeft van een ander type vergelijking

Wanneer de lijn wordt uitgedrukt door een andere dan de impliciete vergelijking, of het nu een vector-, parametrische of continue vergelijking is, verdient het de voorkeur om de methode te gebruiken die we hieronder uitleggen.

Dus als de lijn wordt gegeven in de vorm van een vectorvergelijking, parametervergelijkingen of een continue vergelijking, betekent dit dat we een punt kennen dat bij de lijn hoort, en ook de richtingsvector ervan.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

Aan de andere kant weten we ook wat de normaalvector (of loodrechte) vector op het vlak is:

$\vv{n} \perp \pi$

Vervolgens kan uit de 2 vectoren en het punt van de lijn de relatieve positie tussen de lijn en het vlak als volgt worden berekend:

Als het scalaire product tussen de richtingsvector van de lijn en de vector loodrecht op het vlak verschillend is van nul, betekent dit dat de lijn secans is ten opzichte van het vlak.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
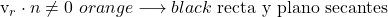
Maar als het scalaire product tussen de richtingsvector van de lijn en de vector loodrecht op het vlak gelijk is aan nul, zijn er twee mogelijkheden: de lijn bevindt zich in het vlak of ze zijn evenwijdig. En om te weten welk geval het is, moeten we de coördinaten van een punt op de lijn vervangen door de vergelijking van het vlak.
- Als het punt voldoet aan de vergelijking van het vlak, bevindt de lijn zich in het vlak.
- Aan de andere kant, als het punt niet voldoet aan de vergelijking van het vlak, zijn de lijn en het vlak evenwijdig.

Voorbeeld van het bepalen van de relatieve positie van een lijn en een vlak met behulp van vectoren

Nadat we de theorie van deze methode hebben gezien, laten we nu een oefening stap voor stap oplossen:

Zoek de relatieve positie tussen de volgende lijn en het volgende vlak:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Ten eerste wordt de lijn gedefinieerd als parametervergelijkingen, dus de richtingsvector en het punt waar de lijn doorheen gaat zijn:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

En aan de andere kant is de vector loodrecht op het vlak:

$\vv{n} =(2,1,-2)$

Zodra we de richtingsvector van de lijn en de vector loodrecht op het vlak kennen, moeten we het scalaire product tussen de twee berekenen:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Het resultaat van het puntproduct is nul, dus de lijn kan alleen in het vlak liggen of evenwijdig daaraan zijn. Om erachter te komen welk geval het is, vervangen we de cartesische coördinaten van het punt op de lijn in de vergelijking van het vlak:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Door het punt van de lijn in de vergelijking van het vlak te vervangen, verkrijgen we een gelijkheid, daarom respecteert het punt de vergelijking van het vlak en bijgevolg bevindt de lijn zich in het vlak .