Relatieve positie van twee lijnen in de ruimte

Hier vind je alle relatieve posities van twee lijnen in de ruimte (in R3). Daarnaast wordt uitgelegd hoe je de relatieve positie tussen twee lijnen kunt vinden met behulp van de twee mogelijke methoden: via bereiken of vanuit een punt en een vector van elke lijn. U kunt zelfs stap voor stap voorbeelden en oefeningen zien die zijn opgelost.

Wat zijn de relatieve posities van twee lijnen in de ruimte?

In analytische meetkunde zijn er bij het werken in een driedimensionale ruimte (in R3) 4 mogelijke relatieve posities tussen twee lijnen: twee lijnen kunnen samenvoegende lijnen , evenwijdige lijnen , secanslijnen of secanslijnen zijn.

Parallelle lijnen

Twee lijnen zijn evenwijdig als ze dezelfde richting hebben, maar geen gemeenschappelijk punt hebben. Bovendien liggen parallelle lijnen altijd op dezelfde afstand van elkaar.

samenvallende lijnen

Twee lijnen vallen samen als ze dezelfde richting hebben en bovendien als al hun punten gemeenschappelijk zijn.

snijdende lijnen

Twee kruisende lijnen hebben verschillende richtingen, maar raken elkaar op één punt.

Snijlijnen

Twee snijdende lijnen hebben verschillende richtingen en kruisen elkaar op geen enkel punt. Daarom liggen twee gekruiste lijnen niet in hetzelfde vlak. Bijvoorbeeld in de grafische weergave boven de lijn

$s$

loopt altijd voorop

$r$

, zodat ze elkaar nooit zullen aanraken.

Er zijn twee manieren om te weten wat de relatieve positie tussen twee lijnen is, aangezien deze afhankelijk zijn van hoe de vergelijkingen van de twee lijnen worden uitgedrukt:

Als de lijnen een vector-, parametrische of continue vergelijkingsvorm hebben, kunt u het beste de relatieve positie berekenen vanuit een punt en een vector van elke lijn (de uitleg van deze methode vindt u hieronder).
Aan de andere kant, als de lijnen worden gedefinieerd in de vorm van impliciete (of algemene) vergelijkingen, is het gemakkelijker om de relatieve positie tussen de twee lijnen te kennen door de rangorde van twee matrices te berekenen (zie de uitleg hieronder).

Bepalen van de relatieve positie van twee lijnen vanuit een punt en een vector

Je kunt vinden welke relatieve positie er is tussen twee lijnen met een punt en een vector van elke lijn. Deze methode is geschikt om te gebruiken wanneer de lijnen worden gedefinieerd in de vorm van een vectorvergelijking, parametervergelijkingen of een continue vergelijking.

Laat de richtingsvector en elk punt op elk van de twee lijnen dus zijn:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Om de relatieve positie van twee lijnen te vinden, moeten we dus de volgende procedure volgen:

‣ Het eerste wat we moeten doen is kijken of de vectoren van de twee lijnen proportioneel zijn of niet, en afhankelijk van het geval doen we het volgende:

Als de twee vectoren proportioneel zijn, kunnen de lijnen evenwijdig zijn of samenvallen. We moeten daarom controleren of het punt van de ene lijn voldoet aan de vergelijking van de andere lijn:
- Als het punt van de ene lijn voldoet aan de vergelijking van de andere lijn, betekent dit dat de twee lijnen samenvallen.
- Anders impliceert dit dat de twee lijnen evenwijdig zijn.
Als de twee vectoren niet proportioneel zijn, kunnen de lijnen elkaar snijden of snijden. In dit geval moeten we de volgende 3×3 determinant oplossen:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Als de vorige determinant gelijk is aan nul, snijden de twee lijnen elkaar in een punt (ze snijden elkaar).
- Als de vorige determinant verschillend is van nul, snijden de twee lijnen elkaar.

De volgende afbeelding vat de hele procedure samen:

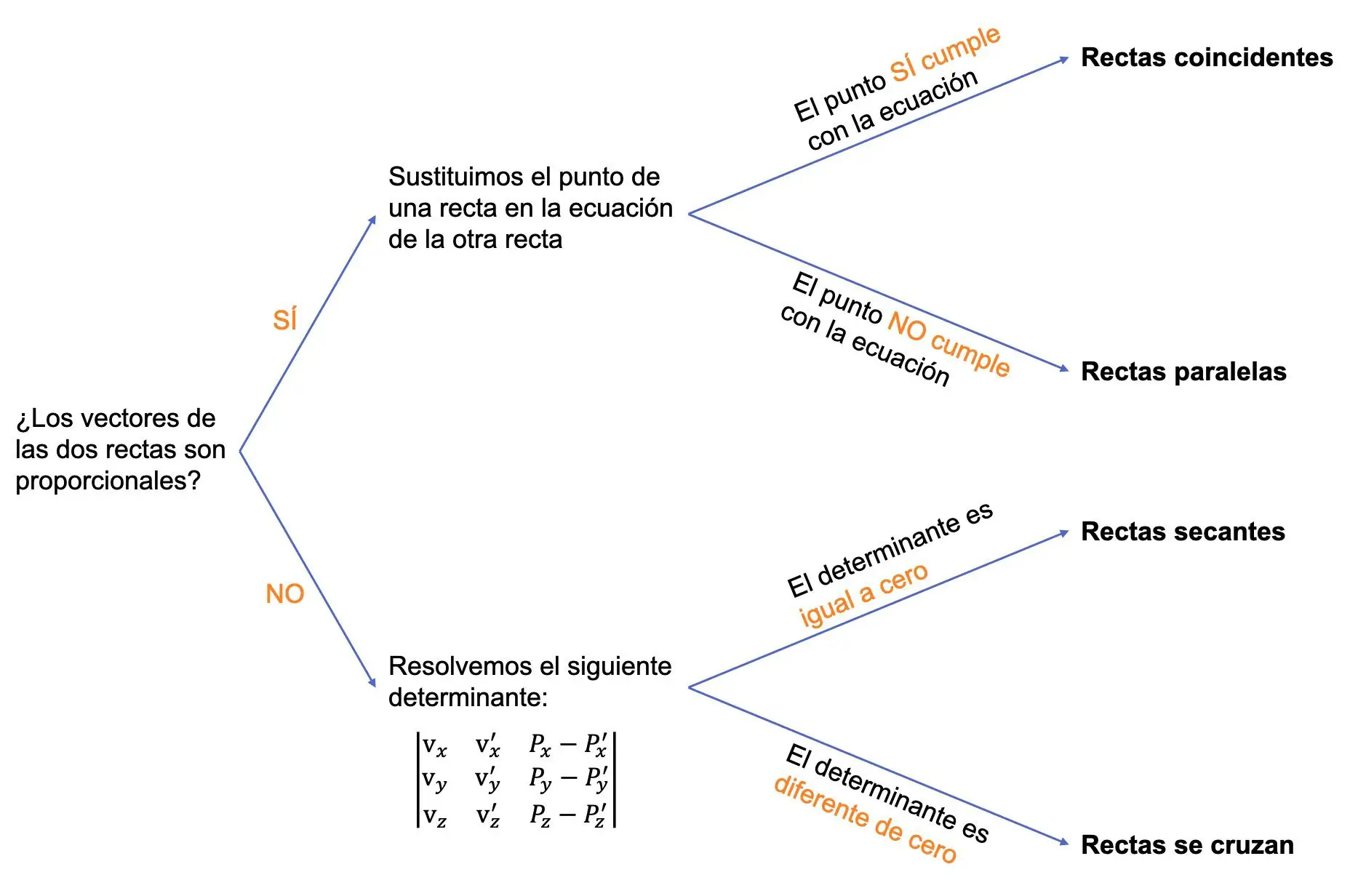
Voorbeeld van het bepalen van de relatieve positie tussen twee lijnen

De vorige procedure lijkt misschien een beetje ingewikkeld, maar zodat u kunt zien dat het tegenovergestelde het geval is, lossen we als voorbeeld een probleem op:

Bepaal de relatieve positie tussen de volgende twee lijnen:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

De twee lijnen worden uitgedrukt als een vectorvergelijking, waarbij de richtingsvector van elke lijn is:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

En een punt waar elke lijn doorheen gaat is:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Zodra we een punt en de richtingsvector van elke lijn kennen, passen we de hierboven beschreven methode toe. Allereerst moeten we controleren of de coördinaten van de vectoren proportioneel zijn:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Omdat de twee vectoren niet evenredig met elkaar zijn, kunnen de lijnen elkaar alleen raken of kruisen. Daarom moeten we nu de volgende determinant oplossen, gevormd door de richtingsvector en een punt op elke lijn:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

We vervangen de waarden in de formule:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

En we berekenen de determinant, hiervoor kunt u elke methode gebruiken (Sarrus-regel, methode van complementen of cofactoren, enz.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Als het resultaat van de bepaling nul zou zijn geweest, zou dit betekenen dat de lijnen elkaar kruisen (ze raken elkaar). Maar de determinant is anders dan 0, dus de lijnen snijden elkaar .

Zoek de relatieve positie van twee lijnen per rij

Een andere manier om de relatieve positie van twee rijen te vinden is door de rangorde van twee betonnen matrices te berekenen, zoals we hierna zullen zien. Deze methode is erg handig als de twee lijnen de vorm van een impliciete (of algemene) vergelijking hebben.

Dus als we twee lijnen hebben uitgedrukt met hun impliciete (of algemene) vergelijkingen in een driedimensionale ruimte (in R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Laat A de matrix zijn die is samengesteld uit de coëfficiënten van de twee lijnen:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

En gegeven de uitgebreide matrix A’, de matrix gevormd door alle parameters van de twee lijnen:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Vervolgens kan de relatieve positie van de twee rijen worden bepaald door het bereik van de twee voorgaande matrices volgens de volgende tabel:

relatieve posities van twee lijnen per rij

Om de relatieve positie tussen twee rijen te vinden, zullen we daarom de rangorde van de twee matrices moeten berekenen en afhankelijk van de rangorde van elke matrix zal het het ene of het andere geval zijn.

Deze stelling kan worden bewezen met behulp van de stelling van Rouché-Frobenius (een methode die wordt gebruikt om stelsels van lineaire vergelijkingen op te lossen), maar op deze pagina zullen we het bewijs niet doen omdat het nogal omslachtig is en niet veel toevoegt.

Voorbeeld van hoe u de relatieve positie van twee lijnen kunt vinden op basis van bereiken

Nadat we de theorie over de relatieve posities tussen twee lijnen per rij hebben gezien, gaan we kijken hoe deze in de praktijk wordt gebracht aan de hand van een voorbeeld:

Zoek de relatieve positie van de volgende twee lijnen:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

De twee lijnen hebben de vorm van algemene (of impliciete) vergelijkingen, dus we zullen de rangschikkingsmethode gebruiken om de relatieve positie tussen de twee lijnen te vinden. We construeren daarom de matrix A en de uitgebreide matrix A’ met de coëfficiënten van de lijnen:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Zodra we beide matrices hebben, moeten we de rangorde van elk berekenen. We berekenen eerst de rangorde van matrix A aan de hand van determinanten:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

Matrix A bevat de determinant van een 3×3-submatrix die niet nul is, dus matrix A heeft rang 3 .

En nu berekenen we de reikwijdte van de uitgebreide matrix A’. De matrix A’ zal altijd minstens de rangorde hebben van de matrix A, die in dit geval 3 waard is, dus het is voldoende om te controleren of deze van rang 4 of van rang 3 is. Om dit te doen, lossen we de determinant op van de 4× matrix 4 door toevoegingen (of cofactoren):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

De determinant van de gehele uitgebreide matrix is nul, dus de matrix A’ is ook van rang 3 .

Dus de matrix A en de matrix A’ hebben rang 3, dus de twee lijnen snijden elkaar . Dat wil zeggen, er is slechts één snijpunt tussen hen.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Bedenk dat je hierboven een tabel hebt die alle mogelijke gevallen van relatieve posities tussen twee lijnen samenvat volgens de bereiken van de matrices A en A’.

Problemen opgelost met de relatieve positie tussen twee lijnen in de ruimte

Oefening 1

Zoek de relatieve positie tussen de volgende twee lijnen:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

zie oplossing

Omdat beide lijnen worden uitgedrukt als een vectorvergelijking, zullen we de relatieve positie tussen de twee lijnen vinden vanuit de één-punt- en één-vectormethode van elke lijn.

De richtingsvector van elke lijn is:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

En een punt dat bij elke lijn hoort is:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Om de procedure toe te passen, moet dus eerst worden gecontroleerd of de componenten van de richtingsvectoren proportioneel zijn:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Omdat de twee vectoren niet evenredig met elkaar zijn, kunnen lijnen elkaar alleen snijden of snijden. Daarom moeten we nu de volgende determinant oplossen, bestaande uit de richtingsvector en een punt op elke lijn:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

We vervangen de waarden in de formule:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

En we berekenen de determinant:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Het resultaat van de bepaler is gelijk aan 0, dus de lijnen snijden .

Oefening 2

Bereken de relatieve positie van de volgende twee lijnen:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

zie oplossing

De eerste lijn heeft de vorm van parametervergelijkingen en de tweede lijn heeft de vorm van een continue vergelijking, waarmee we de relatieve positie tussen de twee lijnen zullen bepalen op basis van de éénpuntsvectormethode van elke lijn.

De coördinaten van de richtingsvector van rechts

$r$

zijn de coëfficiënten vóór de parameter

$t,$

en de coördinaten van de richtingsvector van de lijn

$s$

zijn de getallen van de noemers:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

En een punt dat bij elke lijn hoort is:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Om de procedure toe te passen, moet dus eerst worden gecontroleerd of de componenten van de richtingsvectoren proportioneel zijn:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

De twee vectoren zijn evenredig met elkaar, dus de lijnen kunnen alleen evenwijdig of samenvallend zijn. Om deze twijfel weg te nemen, is het noodzakelijk om het punt op de lijn te vervangen

$r$

in de vergelijking van de lijn

$s$

(of omgekeerd) om te zien of het aan de genoemde vergelijking voldoet:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Door het punt op de lijn te vervangen verkrijgen we een gelijkheid, zodat het punt van de ene lijn voldoet aan de vergelijking van de andere lijn en bovendien zijn hun richtingsvectoren proportioneel. Daarom vallen de twee lijnen samen.

Oefening 3

Zoek de relatieve positie van de volgende twee lijnen:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

zie oplossing

De twee lijnen hebben een algemene (of impliciete) vergelijkingsvorm, dus we zullen de rangschikkingsmethode gebruiken om de relatieve positie tussen de twee lijnen te vinden. We maken daarom de matrix A en de uitgebreide matrix A’ met de coëfficiënten van de lijnen:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Zodra we beide matrices hebben, moeten we de rangorde van elk berekenen. We berekenen eerst de rangorde van matrix A aan de hand van determinanten:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Alle 3×3 determinanten van matrix A zijn nul, maar er bevindt zich een 2×2 determinant die niet nul is in de matrix, dus matrix A heeft rang 2 .

En nu berekenen we de reikwijdte van de uitgebreide matrix A’. De matrix A’ zal altijd minimaal het bereik van matrix A zijn, wat in dit geval 2 is, dus het is noodzakelijk om te controleren of deze een 3×3 determinant heeft die niet opheft en ook hoeveel de determinant is van de gehele matrix:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

De uitgebreide matrix A’ bevat inderdaad 3×3 niet-nul deeldeterminanten en bovendien is de determinant van de gehele uitgebreide matrix gelijk aan 0, dus de matrix A’ heeft rang 3 .

Dus de matrix A heeft rang 2 en de matrix A’ heeft rang 3, dus de twee lijnen zijn evenwijdig . Dat wil zeggen: ze hebben niets met elkaar gemeen.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Bedenk dat je in de uitleg van de methode (hierboven) een tabel hebt die alle mogelijke gevallen van relatieve posities tussen twee lijnen samenvat volgens de rangorde van de matrices A en A’.

Oefening 4

Zoek de relatieve positie van de volgende twee lijnen:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

zie oplossing

In dit geval hebben de twee lijnen de vorm van een cartesiaanse (of impliciete) vergelijking, dus zullen we de ordeningsmethode gebruiken om de relatieve positie tussen de twee lijnen te vinden. We construeren daarom de matrix A en de uitgebreide matrix A’ met de coëfficiënten van de lijnen:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Zodra we de twee matrices kennen, moeten we de rangorde van elk berekenen. We zullen eerst de rangorde van matrix A berekenen aan de hand van determinanten:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

Matrix A bevat een 3×3-submatrix waarvan de determinant niet nul is, dus matrix A heeft rang 3 .

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

De determinant van de gehele uitgebreide matrix is niet nul, dus de matrix A’ heeft rang 4 .

Dus dat de matrix A van rang 3 is en dat de matrix A’ daarentegen van rang 4 is, dus snijden de twee lijnen elkaar in een punt.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Bedenk dat je in de uitleg van de procedure (hierboven) een tabel hebt met alle mogelijke gevallen van relatieve posities tussen twee lijnen volgens de rangorde van de matrices A en A’.

Wat zijn de relatieve posities van twee lijnen in de ruimte?

Bepalen van de relatieve positie van twee lijnen vanuit een punt en een vector

Voorbeeld van het bepalen van de relatieve positie tussen twee lijnen

Zoek de relatieve positie van twee lijnen per rij

Voorbeeld van hoe u de relatieve positie van twee lijnen kunt vinden op basis van bereiken

Problemen opgelost met de relatieve positie tussen twee lijnen in de ruimte

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren