Op deze pagina zie je wat de regel van Cramer is en daarnaast vind je voorbeelden en oefeningen met het oplossen van stelsels vergelijkingen volgens de regel van Cramer.
Wat is de regel van Cramer?
De regel van Cramer is een methode die wordt gebruikt om stelsels vergelijkingen op te lossen met behulp van determinanten. Laten we eens kijken hoe het wordt gebruikt:
Beschouw een systeem van vergelijkingen:
![Rendered by QuickLaTeX.com \begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0141f3451719f665ef28e4061489551_l3.png)
De matrix A en de uitgebreide matrix A’ van het systeem zijn:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d628a13ec7de4b3ba7a301c0a5d8ac6_l3.png)
De regel van Cramer zegt dat de oplossing van een stelsel vergelijkingen is:
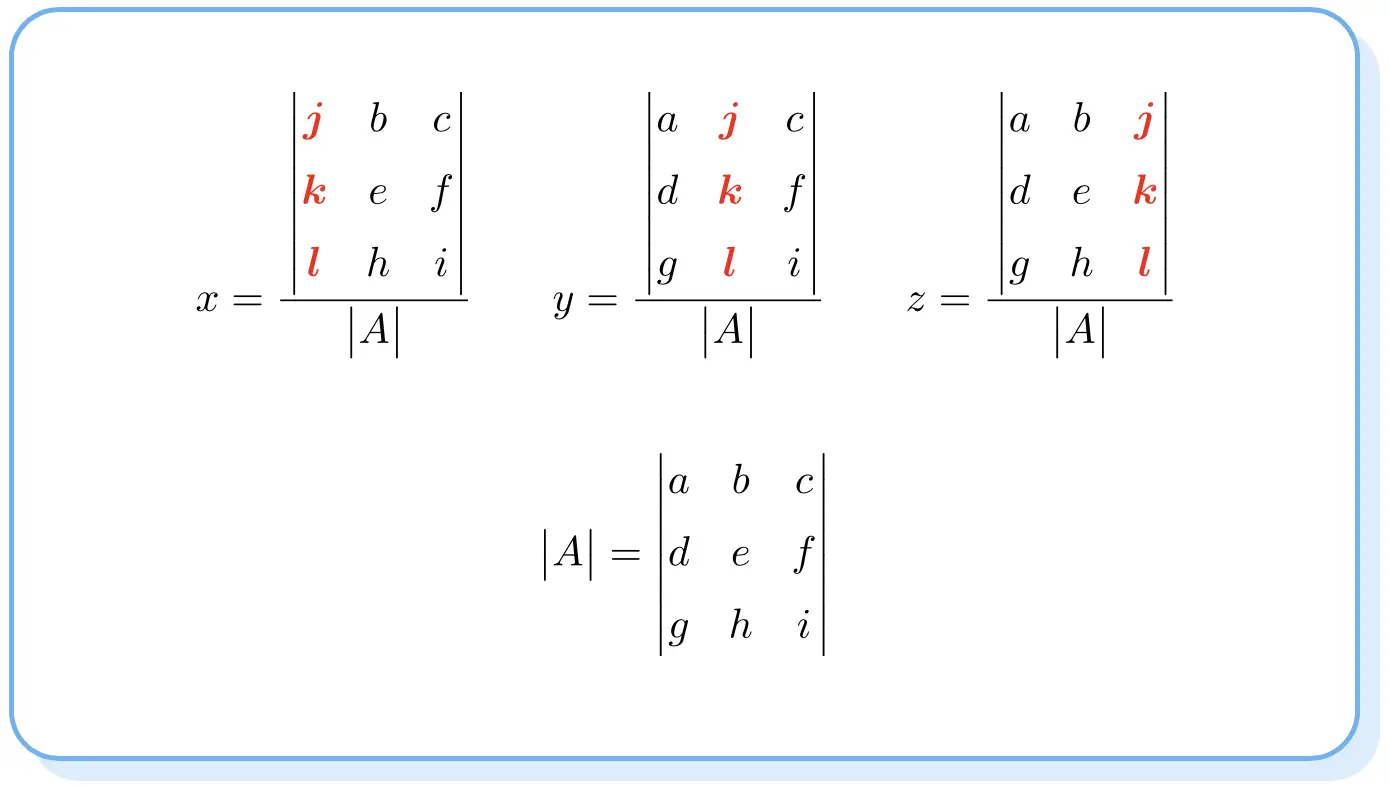
Merk op dat de determinanten van de tellers vergelijkbaar zijn met de determinant van matrix A, maar dat de kolom van elke onbekende verandert in de kolom met onafhankelijke termen.
Daarom wordt de regel van Cramer gebruikt om stelsels van lineaire vergelijkingen op te lossen. Maar zoals je al weet, zijn er veel manieren om een stelsel vergelijkingen op te lossen; de methode van Gauss Jordan is bijvoorbeeld algemeen bekend.
Hieronder staan voorbeelden van het oplossen van stelsels van lineaire vergelijkingen met de regel van Cramer, of soms ook geschreven als de regel van Kramer.
Voorbeeld 1: bepaald compatibel systeem (SCD)
- Los het volgende stelsel van 3 vergelijkingen met 3 onbekenden op met behulp van de regel van Cramer:
![Rendered by QuickLaTeX.com \begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6013b7e73c89c24fe388f1a5d018f32b_l3.png)
We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c710ed86223f47f39b5a25720b5ca19d_l3.png)
We berekenen nu de rangorde van de twee matrices, om te zien wat voor soort systeem het is. Om de rangorde van A te berekenen, berekenen we de 3×3 determinant van de gehele matrix (met behulp van de regel van Sarrus) en kijken of deze 0 oplevert:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae4a3bb88d113494463df8e670c326c6_l3.png)
De determinant van A is anders dan 0, dus matrix A heeft rang 3.
![]()
De matrix A’ heeft dus ook rang 3 , aangezien deze niet rang 4 kan hebben en op zijn minst dezelfde rang moet hebben als matrix A.
![]()
De omvang van de matrix A is gelijk aan de omvang van de matrix A’ en het aantal onbekenden van het systeem (3). Daarom weten we volgens de stelling van Rouché-Frobenius dat het een bepaald compatibel systeem (SCD) is:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Zodra we weten dat het systeem een SCD is, passen we de regel van Cramer toe om het op te lossen. Om dit te doen, bedenk dat de matrix A, zijn determinant en de matrix A’ zijn:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b2b3e5865c2264c360fb887d37a5f6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a604d8f5a3927a47a264d28f7a007b2_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1fa494ffb5e452d59c4d2dad40f925a_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08e3dabe2f33434eb96658491f67c0b4_l3.png)
Berekenen
![]()
Met de regel van Cramer veranderen we de derde kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96e76cb8867224755e9c19254678abd4_l3.png)
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Voorbeeld 2: Onbepaald compatibel systeem (ICS)
- Los het volgende stelsel vergelijkingen op met behulp van de regel van Cramer:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-781530aac4d8507fd6c7cbd77c3b4651_l3.png)
We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a64800a78bf8e2e2f547be907e6863cb_l3.png)
Nu berekenen we het bereik van de twee matrices en kunnen we zo zien welk type systeem het is. Om de rangorde van A te berekenen, berekenen we de determinant van de gehele matrix (met behulp van de regel van Sarrus) en controleren we of deze 0 is:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-581c58cbe0fdd9952e7e25b919ecc33b_l3.png)
De determinant geeft 0, dus matrix A heeft niet rang 3. Maar hij heeft een 2×2 determinant die verschilt van 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Matrix A heeft dus rang 2 :
![]()
Zodra we de omvang van matrix A kennen, berekenen we die van matrix A’. De determinant van de eerste 3 kolommen geeft 0, dus we proberen de andere mogelijke 3×3 determinanten in de matrix A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-686e7ca635ecee685005f6013c2e64ad_l3.png)
Alle determinanten van orde 3 geven 0. Maar uiteraard heeft matrix A’ dezelfde niet-0 2×2 determinant als matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Daarom heeft de matrix A’ ook rang 2 :
![]()
Dus aangezien de rangorde van matrix A gelijk is aan de rangorde van matrix A’, maar deze twee kleiner zijn dan het aantal onbekenden van systeem (3), weten we door de stelling van Rouché-Frobenius dat dit een onbepaald compatibel systeem is. (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Als we een compatibel onbepaald systeem (SCI) willen oplossen, moeten we het systeem transformeren : we elimineren eerst een vergelijking, dan converteren we een variabele naar λ (meestal de variabele z), en tenslotte voegen we de termen met λ samen met de onafhankelijke termen.
Zodra we het systeem hebben getransformeerd, passen we de regel van Cramer toe en krijgen we de oplossing van het systeem als functie van λ.
In dit geval zullen we de laatste vergelijking uit het systeem verwijderen :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0511fecc9c2af695b6b8eccae6b0661_l3.png)
Laten we nu de variabele z naar λ converteren:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d6142d2be611954fd849a032a97245a_l3.png)
En we plaatsen de termen met λ bij de onafhankelijke termen:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00214205f2334f1c9bc10810c1c1df83_l3.png)
Daarom blijven de matrix A en de matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c4b47303973b823a1c5628f5448ca79_l3.png)
Ten slotte passen we, zodra we het systeem hebben getransformeerd, de regel van Cramer toe . We lossen daarom de determinant van A op:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b79f52dc82f5cfc311867273e78c06_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ff917eaea976c65bd18e0476078d3cb_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-155ca520739bbf7e040a6cdc632f7c27_l3.png)
Hoewel de oplossing van het stelsel vergelijkingen een functie is van λ, omdat het een SCI is en daarom oneindig veel oplossingen heeft:
![]()
De regel van Cramer loste problemen op
Oefening 1
Pas de regel van Cramer toe om het volgende stelsel van twee vergelijkingen met twee onbekenden op te lossen:
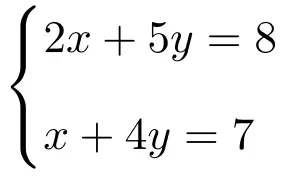
Het eerste wat je moet doen is de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a001db9cf56846150730fee7126dacd_l3.png)
We moeten nu de rangorde van matrix A vinden. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c75c1c344c286016bea83237f1f418e_l3.png)
Omdat de matrix een 2×2 determinant heeft die verschilt van 0, heeft matrix A rang 2:
![]()
Zodra we de rang van A kennen, berekenen we de rang van A’. Dit zal op zijn minst van rang 2 zijn, omdat we zojuist hebben gezien dat er een determinant in zit van orde 2 die verschilt van 0. Bovendien kan het niet van rang 3 zijn, omdat we geen 3×3 determinant kunnen maken. Daarom heeft de matrix A’ ook rang 2:
![]()
Door de stelling van Rouché-Frobenius toe te passen, weten we daarom dat dit een compatibel bepaald systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbd67b16bb6d52a0696e70a77833cd3b_l3.png)
Zodra we weten dat het systeem een SCD is, passen we de regel van Cramer toe om het op te lossen.
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0adeda8f2ce557661466996038b1148_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-59790a66cc31fac07be1d5a7bb556d9e_l3.png)
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Oefening 2
Vind de oplossing van het volgende stelsel van drie vergelijkingen met 3 onbekenden met behulp van de regel van Cramer:
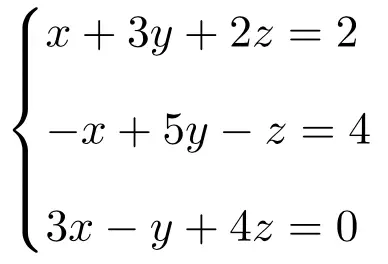
We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-eea75fbf6d86ebc3d0b9e236cd2160f5_l3.png)
We vinden nu de rangorde van matrix A door de determinant van de 3×3 matrix te berekenen met de Sarrusregel:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73f751f3b5c527c16b5de1b10bf07a4e_l3.png)
De matrix heeft een determinant van orde 3 die verschilt van 0, de matrix A heeft rang 3:
![]()
bijgevolg is de matrix A’ ook van rang 3:
![]()
Daarom weten we, met behulp van de stelling van Rouché-Frobenius, dat dit een compatibel bepaald systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Zodra we weten dat het systeem een SCD is, moeten we de regel van Cramer toepassen om het systeem op te lossen.
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc574297f609b68e4fb48466ec6c8077_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2544601137d62e217ff1866f278203d6_l3.png)
Berekenen
![]()
Met de regel van Cramer veranderen we de derde kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42d7d4adcfc48954185ca14b56b8e128_l3.png)
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Oefening 3
Bereken de oplossing van het volgende stelsel van drie vergelijkingen met 3 onbekenden met behulp van de regel van Cramer:
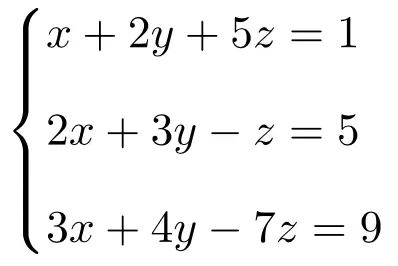
We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-afd359275e5ebaaf3229504c47a5815f_l3.png)
We berekenen de omvang van matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ddf17a2b3eed5a680d685900a79b31_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdd4380c7c76418bd3ec12c94359f886_l3.png)
![]()
Zodra we de omvang van matrix A kennen, berekenen we die van matrix A’. De determinant van de eerste 3 kolommen geeft 0, dus we proberen de andere mogelijke 3×3 determinanten in de matrix A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-1addc62130e0462075b3bade26a7e35e_l3.png)
Alle determinanten van orde 3 geven 0. De matrix A’ heeft echter dezelfde 2×2 niet-0 determinant als de matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7de377466bd5afd03f58f9b532324e75_l3.png)
Daarom heeft de matrix A’ ook rang 2:
![]()
Omdat de rangorde van matrix A gelijk is aan de rangorde van matrix A’, maar deze twee kleiner zijn dan het aantal onbekenden van systeem (3), weten we door de stelling van Rouché-Frobenius dat het een onbepaald compatibel systeem (ICS) is:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Omdat we een ICS-systeem zijn, moeten we een vergelijking elimineren. In dit geval zullen we de laatste vergelijking uit het systeem verwijderen :
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a1d067e155540f4345cf56e5c1567d3_l3.png)
Laten we nu de variabele z naar λ converteren:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5fa91777a722d3783b2f887aab44152_l3.png)
En we plaatsen de termen met λ bij de onafhankelijke termen:
![Rendered by QuickLaTeX.com \begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76ff21181be050b01c247981298986a7_l3.png)
Zodanig dat de matrix A en de matrix A’ van het systeem blijven:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-230e5b28dd467127e63f4f9756cf90da_l3.png)
Ten slotte passen we, zodra we het systeem hebben getransformeerd, de regel van Cramer toe . We lossen daarom de determinant van A op:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1](https://mathority.org/wp-content/ql-cache/quicklatex.com-f127efbd217e2bca8852ec792610732f_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42652a14362b42e606841b6bb3e77cc0_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b95c5870f1762a2d82c9ebcccbca7408_l3.png)
Hoewel de oplossing van het stelsel vergelijkingen een functie is van λ, omdat het een SCI is en daarom oneindig veel oplossingen heeft:
![]()
Oefening 4
Los het volgende probleem op van een stelsel van drie vergelijkingen met drie onbekenden door de regel van Cramer toe te passen:
![Rendered by QuickLaTeX.com \begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e1c3458f33b863db10750b9e51d09e_l3.png)
Eerst construeren we de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-743a40010cb4a610e8a3fc6ae5d313b4_l3.png)
Laten we nu de rangorde van matrix A berekenen door de determinant van de 3×3-matrix te berekenen met behulp van de regel van Sarrus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-713c634fbc3e1b1cb228e3891c9bff1c_l3.png)
De matrix heeft een determinant van orde 3 die verschilt van 0, de matrix A heeft rang 3:
![]()
bijgevolg heeft de matrix A’ ook rang 3, aangezien deze op zijn minst dezelfde rang moet hebben als de matrix A en kan deze niet van rang 4 zijn omdat het een matrix is met dimensie 3×4.
![]()
Daarom leiden we met behulp van de stelling van Rouché-Frobenius af dat het een bepaald compatibel systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Zodra we weten dat het systeem een SCD is, moeten we de regel van Cramer toepassen om het systeem op te lossen.
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a290479c69ff806f19dcf29f96e1228_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bba0765fbcbcebf0585520af25b4a30_l3.png)
Berekenen
![]()
Met de regel van Cramer veranderen we de derde kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bc157a8c4dfe8ee4651affac68ef878_l3.png)
De oplossing voor het stelsel lineaire vergelijkingen is daarom:
![]()
Oefening 5
Los het volgende stelsel lineaire vergelijkingen op met behulp van de regel van Cramer:
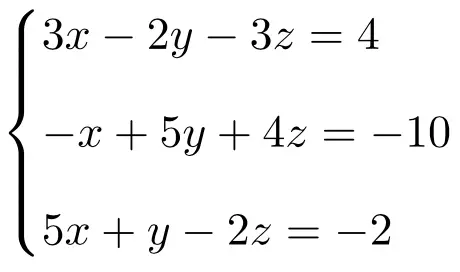
We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5153b5951b768cc3cafa2bb2567ba92_l3.png)
We berekenen de omvang van matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3778c9499e2a44ea3834dfed1523163_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03d70742b14ced92f33963df0c86e92f_l3.png)
![]()
Zodra we de omvang van matrix A kennen, berekenen we die van matrix A’. De determinant van de eerste 3 kolommen geeft 0, dus we proberen de andere mogelijke 3×3 determinanten in de matrix A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bed93d532ae4ccd4649a73662f55f0f_l3.png)
Alle determinanten van orde 3 geven 0. Maar uiteraard heeft matrix A’ dezelfde determinant van orde 2 anders dan 0 als matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-858d95d7d252b16706b66c0e6aba09c4_l3.png)
Daarom heeft de matrix A’ ook rang 2:
![]()
De rangorde van matrix A is gelijk aan de rangorde van matrix A’, maar deze twee zijn kleiner dan het aantal onbekenden van het systeem (3), dus volgens de stelling van Rouché-Frobenius weten we dat het een onbepaald systeemcompatibel (SCI) is. :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Omdat we een ICS-systeem zijn, moeten we één vergelijking elimineren. In dit geval zullen we de laatste vergelijking uit het systeem verwijderen :
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e10bd826663dff41c4272610cbc07b1_l3.png)
Laten we nu de variabele z naar λ converteren:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2502be450040b38761c08e5d6beaf379_l3.png)
En we plaatsen de termen met λ bij de onafhankelijke termen:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80a43d98e6be30965d554e8a89aa5d89_l3.png)
Zodanig dat de matrix A en de matrix A’ van het systeem blijven:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3451ce571163983cf41794d4998283d6_l3.png)
Ten slotte passen we, zodra we het systeem hebben getransformeerd, de regel van Cramer toe . We lossen daarom de determinant van A op:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7a7d6208ea5e762f5c74a44e6838cf_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c30fcc0526c2d4112eb4f60a3d8847f_l3.png)
Om het onbekende te berekenen
![]()
Met de regel van Cramer veranderen we de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdb22a54274e019c811c9051502c474a_l3.png)
De oplossing van het stelsel vergelijkingen is dus een functie van λ, aangezien het een SCI is en het systeem daarom oneindig veel oplossingen heeft:
![]()