Op deze pagina leggen we uit hoe je de regel van Ruffini kunt toepassen om veeltermen te delen. Naast de uitleg kun je voorbeelden en oefeningen zien die stap voor stap zijn opgelost over de delingen van polynomen met de Ruffini-regel. Bovendien vindt u alle toepassingen van deze methode en in feite zullen er meer dan één u zeker verrassen.
Wat is de regel van Ruffini?
In de wiskunde is de regel van Ruffini een algebraïsche methode waarmee je snel een polynoom kunt delen door polynomen van de vorm xr . De regel van Ruffini is vernoemd naar de wiskundige Paolo Ruffini, die deze methode heeft uitgevonden.
De regel van Ruffini wordt echter niet alleen gebruikt voor het delen van polynomen, maar heeft ook vele andere toepassingen. De regel van Ruffini wordt bijvoorbeeld ook gebruikt om de wortels van een polynoom te vinden, om de numerieke waarde van een polynoom te vinden, om een polynoom in factoren te ontbinden, of zelfs om vergelijkingen van de derde graad of hoger op te lossen. Hieronder zullen we zien hoe de regel van Ruffini wordt toegepast om al deze bewerkingen uit te kunnen voeren.
Ten slotte staat de regel van Ruffini ook bekend als de methode van Ruffini, de stelling van Ruffini of de synthetische verdeling van polynomen.
Hoe de regel van Ruffini toe te passen
Zoals we hebben gezien, is het voornaamste gebruik van de regel van Ruffini het delen van een polynoom door een binomiaal, dat wil zeggen het maken van een deling van het volgende type:
![]()
Merk op dat om de regel van Ruffini te gebruiken , het delende polynoom altijd moet worden gevormd door een x (met een coëfficiënt gelijk aan 1) en een getal (positief of negatief), anders kan het Ruffini-algoritme niet worden gebruikt.
Om de regel van Ruffini toe te passen moet een hele procedure worden gevolgd, dus hieronder zullen we stap voor stap een voorbeeld oplossen om te zien hoe de regel van Ruffini (of de methode van Ruffini) wordt toegepast.
Voorbeeld van de regel van Ruffini
- Los de volgende verdeling van polynomen op met behulp van de regel van Ruffini:
![]()
Allereerst moet je twee loodrechte lijnen tekenen die elkaar snijden, en vervolgens het deeltal en de deler als volgt plaatsen:
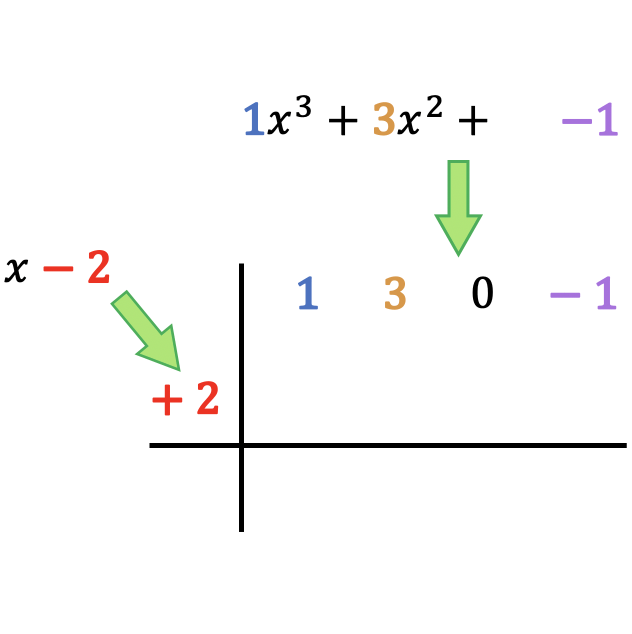
Zoals je kunt zien, moeten we de coëfficiënten van het dividendpolynoom bovenaan plaatsen, geordend van de hoogste graad naar de laagste, en we plaatsen de onafhankelijke term van het delerpolynoom links van de doos met een verandering van teken .
Waarschuwing: Als het dividendpolynoom geen looptijd van een bepaalde graad heeft (onvolledig polynoom), wordt er een 0 voor in de plaats gezet. In dit geval bijvoorbeeld de polynoom
![]()
Het heeft geen monomial van graad 1, dus zetten we er een 0 voor in de plaats.
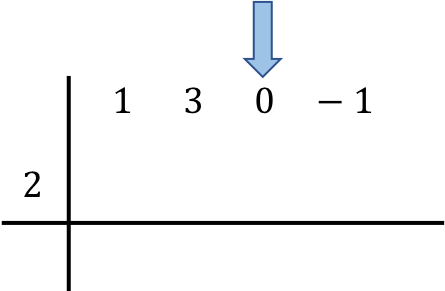
Zodra we de polynomen die bij de bewerking betrokken zijn, hebben gepositioneerd, verlagen we het eerste getal rechtstreeks naar de onderstaande regel:
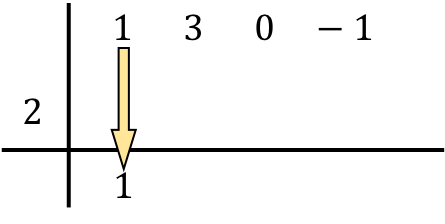
Nu komt de stap die de regel van Ruffini kenmerkt: we vermenigvuldigen het onderstaande getal met het getal aan de linkerkant en plaatsen het resultaat in de volgende kolom :
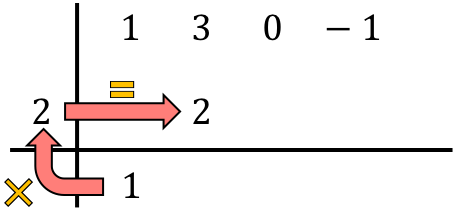
En we voegen de getallen in de kolom toe, waarbij het resultaat van de som er net onder staat:
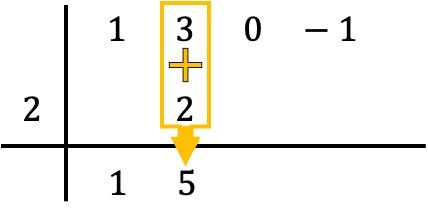
De methode van Ruffini houdt dus in dat dit proces wordt herhaald. We doen dus opnieuw hetzelfde: we vermenigvuldigen het onderste getal met het getal aan de linkerkant, we plaatsen het resultaat in de volgende kolom en ten slotte voegen we de getallen toe die verticaal uitgelijnd zijn:
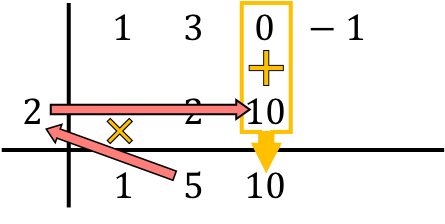
En we herhalen dezelfde procedure achtereenvolgens tot het einde. We berekenen eerst het product van het onderstaande getal met het getal aan de linkerkant, daarna plaatsen we het resultaat in de volgende kolom en ten slotte tellen we de getallen in dezelfde kolom op:
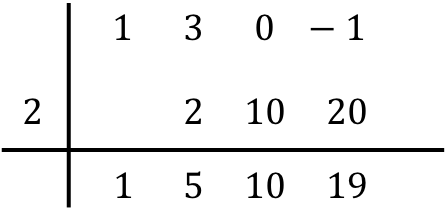
Dus als we alle kolommen hebben gevuld, betekent dit dat we klaar zijn met het delen van de polynomen.
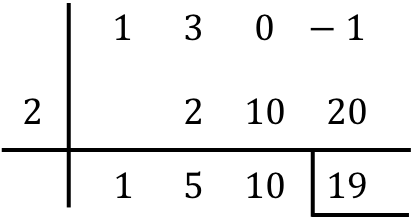
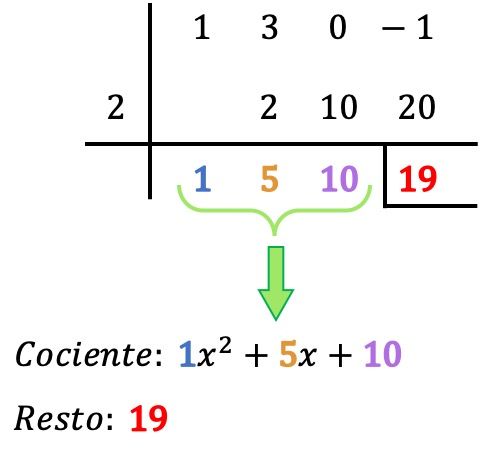
Je hoeft dus alleen maar het resultaat te vinden van het delen van de polynomen:
- De rest van de verdeling tussen de twee polynomen is het laatste getal in de onderstaande regel, dus in ons geval is de rest gelijk aan 19. De rest wordt meestal aangegeven door een balk links te plaatsen en een andere onder dat getal.
- Het quotiënt van de polynoomdeling wordt bepaald door de andere verkregen waarden, namelijk de coëfficiënten van het polynoomquotiënt. Het eerste cijfer van rechts komt overeen met de coëfficiënt van de term van graad 0, het volgende cijfer is de coëfficiënt van de term van graad 1, het volgende van graad 2, het volgende van graad 3,… enzovoort tot het einde. . DUS:
Opgeloste oefeningen van Ruffini’s heerschappij
Hieronder vindt u verschillende opgeloste stapsgewijze oefeningen over de regel van Ruffini, zodat u kunt oefenen en begrijpen hoe u deling van polynomen met deze methode kunt oplossen. We raden u aan elke oefening uit te proberen en vervolgens te controleren of u deze correct hebt uitgevoerd door naar de correctie te kijken.
Oefening 1
Voer de volgende verdeling van polynomen uit met de regel van Ruffini:
![]()
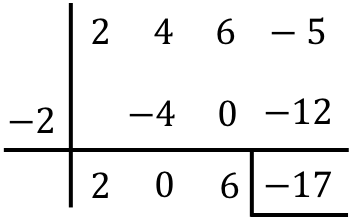
Het resultaat van de deling tussen de twee polynomen is daarom:
Quotiënt:
![]()
Rest:
![]()
Oefening 2
Bereken de volgende verdeling van polynomen met behulp van de regel van Ruffini:
![]()
In dit specifieke geval heeft het dividendpolynoom geen term van de tweede graad, we moeten daarom een nul op zijn plaats zetten:
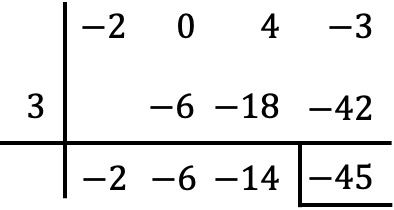
Het resultaat van de deling tussen de 2 polynomen is daarom:
Quotiënt:
![]()
Rest:
![]()
Oefening 3
Zoek het resultaat van de volgende deling van polynomen volgens de regel van Ruffini:
![]()
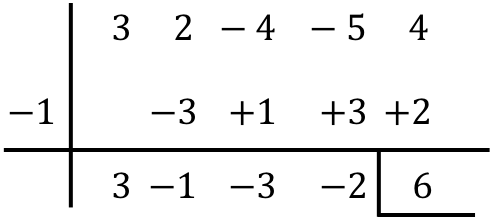
Concluderend is het resultaat van het delen van de twee polynomen:
Quotiënt:
![]()
Rest:
![]()
Oefening 4
Zoek de waarde van de onbekende m zodat de rest van de volgende deling van de polynomen gelijk is aan 5:
![]()
Omdat de deler de vorm (xr) of (x+r) heeft, kunnen we de regel van Ruffini toepassen om de deling op te lossen. We passen daarom de methode van Ruffini toe door de onbekende m te slepen:
Nu maken we de verkregen rest gelijk aan 5, omdat de rest 5 moet zijn:
![]()
En we lossen de vergelijking op om de waarde van de parameter m te vinden:
![]()
![]()
Dus als de variabele m gelijk is aan 3, zal de rest van de verdeling tussen de polynomen gelijk zijn aan 5.
Oefening 5
Bepaal de waarde van de parameter m zodat de rest van de volgende polynomiale deling 3 oplevert:
![]()
Omdat de deler de vorm (xr) of (x+r) heeft, kunnen we de regel van Ruffini toepassen om de deling op te lossen. Daarom gebruiken we de methode van Ruffini door de onbekende m te slepen:
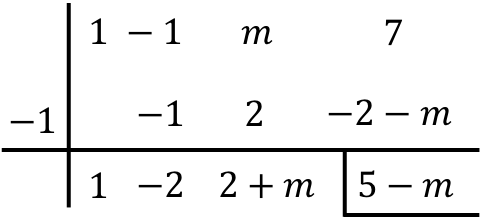
Houd bij de laatste vermenigvuldiging rekening met de distributieve eigenschap:
![]()
Aan de andere kant is de berekening van de rest van de verdeling:
![]()
![]()
![]()
We maken nu de resulterende restuitdrukking gelijk aan 3, aangezien de rest van de deling gelijk moet zijn aan 3:
![]()
En we lossen de resulterende vergelijking op om de waarde van de parameter m te bepalen:
![]()
![]()
![]()
![]()
Daarom moet m gelijk zijn aan 2 zodat de rest van de polynoomdeling gelijk is aan 3.
Meer toepassingen van de regel van Ruffini
Zoals uitgelegd wordt de regel van Ruffini voornamelijk gebruikt om deling tussen polynomen uit te voeren. De regel van Ruffini wordt echter ook gebruikt om andere berekeningen uit te voeren, we zullen ze hieronder allemaal zien.
Wortels van een polynoom
De wortels van een polynoom kunnen eenvoudig worden bepaald met behulp van de regel van Ruffini. Als je niet weet wat de wortel van een polynoom is, laten we dan de definitie ervan eens bekijken:
De wortels (of nullen) van een polynoom zijn de waarden die de polynoom opheffen. Of met andere woorden: de wortels van een polynoom zijn al die waarden die, wanneer ze in de polynoom worden geëvalueerd, een numerieke waarde gelijk aan 0 hebben.
![]()
Aan de andere kant weten we dankzij de reststelling dat als de numerieke waarde van een polynoom voor een gegeven waarde
![]()
nul is, noodzakelijkerwijs de rest van de verdeling van genoemde polynoom tussen
![]()
Het moet ook 0 zijn.
![]()
Daarom, als je de regel van Ruffini gebruikt om een polynoom te delen
![]()
tussen een andere polynoom van de vorm
![]()
we krijgen een rest gelijk aan 0, dit betekent dat
![]()
is een wortel van de polynoom
![]()
Met een voorbeeld zullen we het zeker beter begrijpen:
- Controleer of
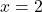
is een wortel van de polynoom
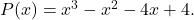
Om te controleren of de gegeven waarde een wortel is van de polynoom, past u eenvoudigweg de Ruffini-methode toe met genoemde polynoom en genoemde waarde:
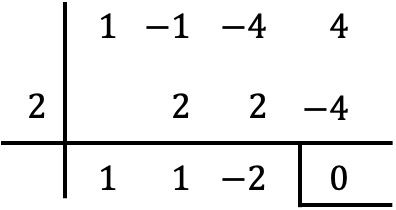
Aangezien de rest verkregen door de regel van Ruffini gelijk is aan nul, betekent dit dat feitelijk
![]()
is een wortel van de polynoom
![]()
Veeltermen ontbinden in factoren
De regel van Ruffini is de methode die gewoonlijk wordt toegepast op factoriële polynomen, omdat je hiermee snel alle wortels kunt kennen van een polynoom van graad 3, 4, 5, enz.
Laten we dus eens kijken hoe we een polynoom kunnen factoriseren met het algoritme van Ruffini aan de hand van een voorbeeld:
- Factor de volgende polynoom van de derde graad:
![]()
Het eerste dat u moet doen, is alle wortels van de polynoom vinden. En de mogelijke wortels van een polynoom zijn de delers van de onafhankelijke term, die in dit geval 6 is. Dus:
Mogelijke wortels van de polynoom: +1, -1, +2, -2, +3, -3, +6, -6
We moeten nu proberen de polynoom tussen elk van deze waarden te verdelen met de regel van Ruffini. Als de rest van de deling 0 is, betekent dit dat de waarde een wortel is van de polynoom; Als de rest van de deling echter niet 0 is, is de waarde geen wortel van de polynoom. Het testen van de regel van Ruffini met alle getallen annuleert dus alleen de rest in de volgende drie gevallen:
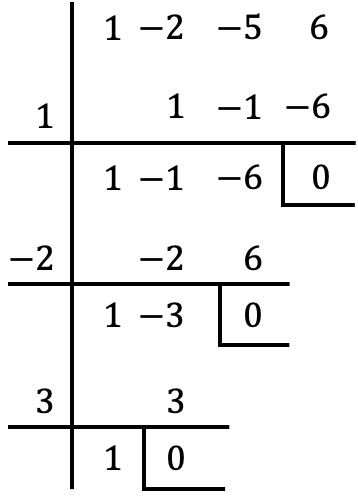
Daarom zijn de wortels van de polynoom in het probleem de waarden waarmee de rest verdwijnt, dat wil zeggen:
![]()
Ten slotte moeten we, om de polynoom in factoren te ontbinden, elke wortel uitdrukken
![]()
in de vorm van een factor van het type
![]()
, dat wil zeggen dat je voor elke wortel een haakje met a moet plaatsen
![]()
en de gevonden wortel is van teken veranderd:
![]()
Zoals u kunt zien, hebben we de polynoom met succes ontbonden met behulp van de regel van Ruffini. Het kan echter zijn dat u twijfels heeft gehad over het factoriseren van polynomen, omdat het een zeer complex onderwerp is. In dit geval kun je op onze website (in de zoekmachine rechtsboven) zoeken naar het artikel dat we hebben over het ontbinden van polynomen , daar leggen we het nader uit en kun je er stap voor stap mee oefenen. Daarnaast laten we u ook andere methoden zien om polynomen te ontbinden.
Bereken de numerieke waarde van een polynoom
Hoewel het misschien verrassend lijkt, kan de numerieke waarde van een polynoom worden bepaald door de regel van Ruffini met behulp van de reststelling.
Maar hiervoor moet je uiteraard de reststelling kennen. Mocht dit niet het geval zijn, dan kun je op onze website (in de zoekmachine rechtsboven) de uitleg van de reststelling opzoeken .
Dankzij de reststelling kunnen we dus de numerieke waarde van elke polynoom kennen. Laten we eens kijken hoe we dit kunnen doen aan de hand van een voorbeeld:
- Bereken de numerieke waarde van

Voor
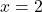
het toepassen van de regel van Ruffini, zijnde
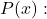
![]()
Om de numerieke waarde van de polynoom voor de waarde te vinden
![]()
Het enige dat we hoeven te doen is de regel van Ruffini gebruiken met de polynoom en de volgende waarde:
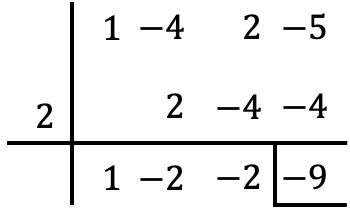
Uit de reststelling weten we dus dat de numerieke waarde van de polynoom samenvalt met de rest van de polynoomverdeling . Daarom is de numerieke waarde van de polynoom in
![]()
is -9.
![]()
Aan de andere kant kunnen we verifiëren dat de regel van Ruffini correct wordt toegepast door de numerieke waarde numeriek te berekenen:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Los vergelijkingen van de derde graad of hoger op
Een andere toepassing van de regel van Ruffini is het oplossen van vergelijkingen met een graad groter dan 2, aangezien er in deze gevallen geen formule bestaat zoals in de tweedegraadsvergelijking. Laten we eens kijken hoe we dit kunnen doen aan de hand van een voorbeeld:
- Los de volgende kwadratische vergelijking op met behulp van de regel van Ruffini:
![]()
We moeten de vergelijking behandelen alsof het een polynoom is. Vervolgens moeten we zoveel mogelijk wortels van het ‘polynoom’ berekenen met behulp van de regel van Ruffini, totdat we een tweedegraadsvergelijking verkrijgen . In dit geval is het een vergelijking van graad 3, het is dus voldoende om een wortel van de “polynoom” te bepalen:
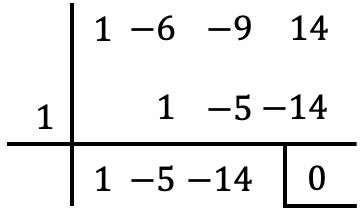
Een oplossing van de vergelijking zal daarom zijn
![]()
Om de andere oplossingen te vinden, moeten we de verkregen polynoom in het quotiënt van de regel van Ruffini gelijk stellen aan 0:
![]()
En nu lossen we de resulterende kwadratische vergelijking op met de bijbehorende formule:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
Concluderend zijn de 3 oplossingen van de derdegraadsvergelijking:
![]()