Rationele functie: wat is het, domein, asymptoten, grafiek, oefeningen,...

Hier ontdek je wat rationale functies zijn. Daarnaast leggen we uit hoe je het domein en de asymptoten van een rationale functie kunt berekenen. En niet alleen dat, maar u zult zien wat alle kenmerken van rationale functies zijn. Ten slotte kun je oefenen met stapsgewijze oefeningen over rationele functies.

Wat is een rationele functie?

De definitie van een rationale functie is als volgt:

Een rationale functie is een functie die wordt gevormd door het quotiënt van twee polynomen , dat wil zeggen dat een rationale functie een breuk is met een polynoom in de teller en de noemer.

Rationele functies worden gekenmerkt door singulariteiten op de punten waar de noemer verdwijnt.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Rationele functies worden ook wel fractionele functies genoemd.

Aan de andere kant moeten rationele functies niet worden verward met irrationele functies. Irrationele (of radicale) functies zijn functies die uit wortels bestaan.

Voorbeelden van rationele functies

Om het begrip rationele functie beter te begrijpen, zullen we verschillende voorbeelden van dit type functie zien.

Rationele functie met een polynoom van de eerste graad in de teller en de noemer:

$f(x)=\cfrac{x+3}{2x-5}$

Dit soort rationale functies worden ook wel homograaffuncties genoemd.

Rationele functie met een constante in de teller en een polynoom in de noemer:

$f(x)=\cfrac{7}{x+1}$

Dit soort rationale functies worden invers proportionele functies genoemd en worden gebruikt om omgekeerd proportionele grootheden wiskundig te definiëren.

Rationele functie met een polynoom van de derde graad in de teller en een polynoom van de tweede graad in de noemer:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Domein van een rationale functie

Een getal gedeeld door 0 is een onbepaaldheid die oneindigheid (∞) oplevert, dus er zal altijd een rationale functie bestaan tenzij de noemer 0 is.

Daarom bestaat het domein van een rationale functie uit alle reële getallen behalve waarden die de noemer opheffen.

Om het domein van een rationale functie te krijgen, moeten we dus uitzoeken wanneer de noemer 0 is, aangezien dit punt het enige punt zal zijn dat niet tot het domein behoort.

Laten we eens kijken hoe het domein van een rationale functie wordt berekend door een voorbeeld op te lossen:

$f(x)=\cfrac{5x}{x+2}$

We stellen eerst de noemer gelijk aan 0 en lossen vervolgens de resulterende vergelijking op:

$x+2=0$

$x=-2$

Wanneer x -2 is, zal de noemer dus 0 zijn en zal de functie dus niet bestaan. Het domein van de functie bestaat dus uit alle reële getallen behalve x=-2. Dit wordt als volgt vermeld:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Asymptoten van een rationele functie

Een van de belangrijkste eigenschappen van rationale functies zijn hun asymptoten, aangezien ze hun grafische weergave bepalen.

➤ Zie:grafische weergave van een functie

De asymptoten van een rationale functie zijn lijnen die de grafiek van de functie voor onbepaalde tijd benadert maar nooit raakt.

Er zijn drie soorten asymptoten: verticale asymptoten, horizontale asymptoten en schuine asymptoten.

Hieronder zie je de drie soorten asymptoten die een rationale functie in rood kan weergeven.

Verticale asymptoot van een rationale functie

Horizontale asymptoot van een rationale functie

Schuine asymptoot van een rationale functie

Zoals je kunt zien, is het bepalen van de asymptoot van een functie aan de hand van de grafiek vrij eenvoudig, maar het berekenen van de asymptoten van een rationale functie zonder dat de grafiek ervan wordt weergegeven, is behoorlijk ingewikkeld. Daarom raden wij u aan om op onze website te bekijken hoe de asymptoten van een functie worden berekend.

Kenmerken van een rationele functie

Rationele functies hebben de volgende kenmerken:

$f(x)=\cfrac{P(x)}{Q(x)}$

Zoals we hierboven zagen, omvat het domein van rationale functies alle reële getallen behalve waarden die de noemer van de breuk opheffen.

Over het algemeen omvat het bereik (of bereik) van een rationale functie alle reële getallen behalve waarden waarin de functie een horizontale asymptoot heeft.

Rationele functies zijn continu in hun hele domein. Met andere woorden: rationele functies vertonen discontinuïteiten op punten die niet tot hun domein behoren.

De grafische weergave van de meeste rationele functies bestaat uit twee hyperbolen.

Sommige regels voor de asymptoten van rationale functies kunnen worden afgeleid uit de polynoomteller.
$P(x)$

en de noemerpolynoom

$Q(x):$
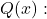
- Een rationale functie heeft een verticale asymptoot op de punten waar de wortels van liggen
  $Q(x)$
  
  maar dit zijn geen wortels van
  
  $P(x).$
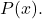
- Als de graad van
  $P(x)$
  
  is kleiner dan de graad van
  
  $Q(x)$
  
  , de lijn y=0 is een horizontale asymptoot van de rationale functie.
- Als de graad van
  $P(x)$
  
  groter is dan de graad van
  
  $Q(x)$
  
  , heeft de rationale functie geen horizontale asymptoot.
- Als de graad van
  $P(x)$
  
  is een eenheid groter dan de graad van
  
  $Q(x)$
  
  en de twee polynomen geen gemeenschappelijke wortel hebben, heeft de rationale functie een schuine asymptoot.

Opgeloste oefeningen over rationele functies

Oefening 1

Zoek het domein van de volgende rationale functie:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Zie de oplossing

Het is een rationale functie, dus het domein bestaat uit alle getallen behalve de getallen die de noemer opheffen, want dan zou de functie ∞ opleveren.

Dus stellen we de noemer van het gehele getal gelijk aan nul om te zien welk getal niet tot het domein behoort:

$2x+4=0$

En we lossen de resulterende vergelijking op:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Het domein van de functie bestaat daarom alleen uit getallen behalve -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Oefening 2

Zoek de afkappunten van de volgende rationale functie met de cartesiaanse assen:

$f(x)=\cfrac{x^2-9}{x}$

Zie de oplossing

Snijpunt met X-as

Om het snijpunt van de functie met de X-as te vinden, is het noodzakelijk om op te lossen

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

We hebben twee oplossingen van de kwadratische vergelijking verkregen, dus de rationale functie snijdt de abscis-as op twee verschillende punten, namelijk:

$\bm{(3,0)\qquad (-3,0)}$

Snijpunt met Y-as

Om het snijpunt met de Y-as te vinden, moet u berekenen

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Elk getal gedeeld door nul is een onbepaaldheid die oneindigheid oplevert. Daarom passeert de rationale functie op geen enkel punt boven de Y-as, dat wil zeggen dat deze geen snijpunt heeft met de y-as.

Oefening 3

Teken de volgende rationale functie in een grafiek:

$y=\cfrac{2x+3}{2x+6}$

Zie de oplossing

Het eerste dat u moet doen, is het domein van de functie berekenen:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Zodra we het domein van de functie kennen, construeren we een tabel met waarden:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Om te eindigen, geeft u eenvoudigweg de verkregen punten weer in een grafiek en tekent u de hyperbolen, waarmee u de rationale functie tekent:

Oefening 4

Bepaal de asymptoten van de onderstaande rationale functie:

Zie de oplossing

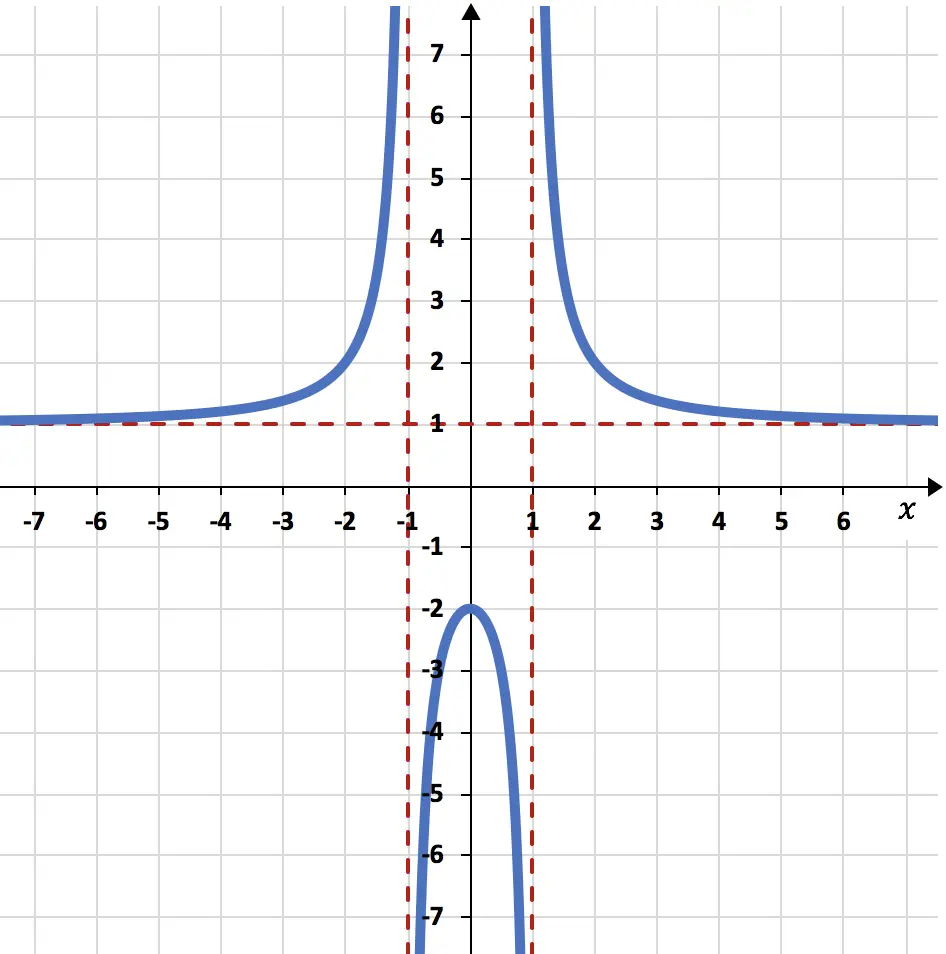
De asymptoten zijn heel duidelijk zichtbaar in de grafiek, omdat ze worden weergegeven als rode stippellijnen.

In dit probleem ligt de functie heel dicht bij de horizontale lijn y=1, maar raakt deze nooit. Daarom heeft de rationale functie één enkele horizontale asymptoot, namelijk y = 1.

Op dezelfde manier ligt de grafische weergave van de functie zeer dicht bij de verticale lijnen x=-1 en x=1, maar bereikt deze waarden nooit. De rationale functie heeft daarom twee verschillende verticale asymptoten, namelijk x=-1 en x=1.

Oefening 5

Bereken alle asymptoten van de volgende rationale functie:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Let op: Om deze oefening op te lossen raden wij u aan eerst naar de bovenstaande link te gaan over hoe de asymptoten van een functie worden berekend en de uitleg te bekijken.

Zie de oplossing

verticale asymptoot

Om de verticale asymptoten van een functie te berekenen, moeten we eerst het domein van de functie vinden. Daarom stellen we de noemer van de rationale functie gelijk aan 0 om de punten te vinden die niet tot het domein behoren:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Het domein van de functie bestaat dus uit alle getallen behalve -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Dus x=-1 zou een verticale asymptoot kunnen zijn. Om dit te controleren, moeten we de limiet van de functie op het punt berekenen:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Daarom is x=-1 een verticale asymptoot van de rationale functie, aangezien de limiet van de functie op dit punt oneindigheid oplevert.

horizontale asymptoot

Om de horizontale asymptoten te bepalen, moeten we de oneindige limiet van de functie berekenen:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

In dit geval is het resultaat van de onbepaalde oneindige limiet tussen oneindigheid de verdeling van de coëfficiënten van de x van de hoogste graad, aangezien de teller en de noemer van dezelfde orde zijn.

De twee oneindige grenzen van de functie gaven ons 3, dus y=3 is een horizontale asymptoot van de rationale functie.

schuine asymptoot

Omdat er een horizontale asymptoot is, heeft de rationale functie geen schuine asymptoot.

Wat is een rationele functie?

Voorbeelden van rationele functies

Domein van een rationale functie

Asymptoten van een rationele functie

Kenmerken van een rationele functie

Opgeloste oefeningen over rationele functies

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren