Vermenigvuldiging van een vector met een getal

Op deze pagina wordt uitgelegd hoe u een vector numeriek en grafisch kunt vermenigvuldigen met een reëel getal (of een scalair). Daarnaast vind je ook voorbeelden en opgeloste oefeningen van het product van een vector door een scalair. Tenslotte worden ook de eigenschappen van dit soort operaties met vectoren toegelicht.

Hoe vermenigvuldig je een vector met een reëel getal?

Om het product van een vector en een getal (of een scalair) numeriek te berekenen, moet elke component van de vector met het getal worden vermenigvuldigd.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

$k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y)$

Het resultaat van het vermenigvuldigen van een vector met een getal geeft dus aanleiding tot een nieuwe vector met de volgende kenmerken:

Het resultaat van het product van een vector door een scalair levert een nieuwe vector op met dezelfde richting als de oorspronkelijke vector.
Bovendien zal de nieuwe vector dezelfde richting hebben als het getal positief is.
Of het heeft de tegenovergestelde betekenis als het getal negatief is.
De grootte van de resulterende vector is equivalent aan de grootte van de oorspronkelijke vector maal de scalair.

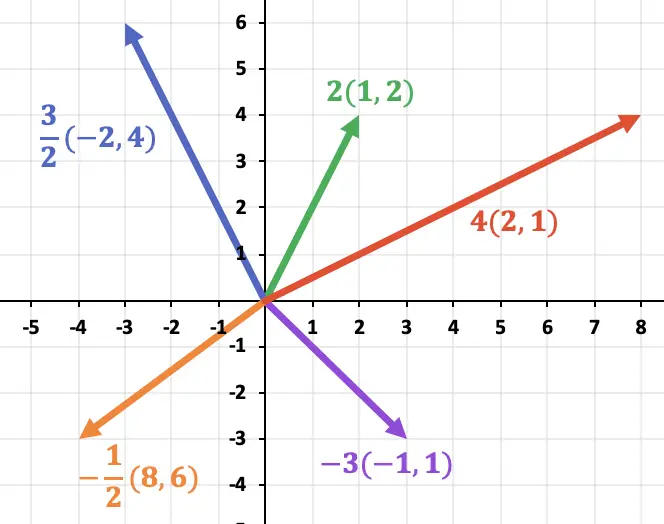
In de volgende grafiek kun je zien hoe de richting van de vector behouden blijft, ongeacht het teken van de scalaire waarde. Aan de andere kant hangt de richting van de vector af van het teken van het getal dat hij vermenigvuldigt.

vermenigvuldiging of product van een getal of scalair met een vector

Bovendien is in de volgende grafiek duidelijk te zien dat de grootte van de resulterende productvector gelijk is aan de grootte van de oorspronkelijke vector vermenigvuldigd met de scalair.

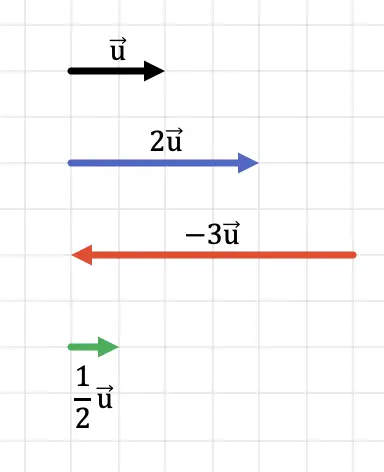
Hoe evolueert de module van een vermenigvuldiging of product van een getal met een vector?

Het is duidelijk dat als we de vector vermenigvuldigen met een getal groter dan 1, het resultaat een vector is met een grotere lengte (met een grotere modulus). Aan de andere kant, als we de vector vermenigvuldigen met een getal kleiner dan 1, dan is het resultaat een vector met een kortere lengte (kleinere modulus).

Opmerking: Verwar het product van een vector en een scalair niet met het puntproduct van vectoren . Hoewel ze een vergelijkbare naam hebben, zijn het twee totaal verschillende concepten.

Voorbeeld van een product van een vector door een scalair

Vervolgens zien we een numeriek voorbeeld van hoe het product van een vector en een getal wordt berekend:

Vermenigvuldig de volgende vector met 4:

$\vv{\text{u}} =(2,-3)$

$4\cdot \vv{\text{u}} =(4 \cdot 2 \ , \ 4 \cdot (-3)) = \bm{(8,-12)}$

Zoals je hebt gezien is dit type vectorbewerking niet erg ingewikkeld, omdat je niet veel berekeningen hoeft uit te voeren.

Er zijn echter ingewikkelder vectorbewerkingen, zoals vectoroptelling en vectoraftrekking. Als u al heeft begrepen hoe u het product van een vector en een scalair moet berekenen, raden we u aan naar het volgende niveau te gaan en te zien hoe u vectoroptelling en vectoraftrekking kunt oplossen, aangezien dit wat moeilijkere bewerkingen zijn en, in feite, ze worden veel vaker gebruikt (ze zijn belangrijker).

Eigenschappen van het vermenigvuldigen van een vector met een getal

Het product van een vector en een getal heeft de volgende eigenschappen:

Associatieve eigenschap : Wanneer de vector met meer dan één getal wordt vermenigvuldigd, doet de volgorde van de vermenigvuldigingen er niet toe.

$k \cdot (k' \cdot \vv{\text{u}}) =(k\cdot k') \cdot \vv{\text{u}}$

Distributieve eigenschap met betrekking tot het optellen en aftrekken van vectoren:

$k \cdot (\vv{\text{u}}+ \vv{\text{v}})=k\cdot \vv{\text{u}} + k\cdot \vv{\text{v}}$

$k \cdot (\vv{\text{u}}- \vv{\text{v}})=k\cdot \vv{\text{u}} - k\cdot \vv{\text{v}}$

Distributieve eigenschap met betrekking tot de toevoeging van scalairen:

$(k+k') \cdot \vv{\text{u}} =k\cdot \vv{\text{u}} + k'\cdot \vv{\text{u}}$

Neutraal element : Uiteraard geeft elke vector vermenigvuldigd met 1 de vector zelf:

$1\cdot \vv{\text{u}} = \vv{\text{u}}$

Opgeloste problemen van vermenigvuldiging van een vector met een scalair

Oefening 1

Bereken analytisch het resultaat van het product van de volgende vector met 3:

$\vv{a}=(-2,5)$

zie oplossing

Om het product te vinden, moet je elke coördinaat van de vector met 3 vermenigvuldigen:

$3\cdot \vv{a}=(3\cdot (-2), 3 \cdot 5) = \bm{(-6,15)}$

Oefening 2

Vermenigvuldig de volgende vector met 6 en vind de module ervan:

$\vv{a}=(3,-4)$

zie oplossing

We vermenigvuldigen eerst de vector met de scalair:

$6\cdot \vv{a}=(6\cdot 3, 6 \cdot (-4)) = (18,-24)$

Er zijn nu twee manieren om de grootte van de verkregen vector te berekenen. De eerste is om de grootte van de oorspronkelijke vector te vinden en deze vervolgens met 6 te vermenigvuldigen:

$\lvert \vv{a} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{25} =5$

$6\cdot \lvert \vv{a} \rvert =6\cdot 5 =\bm{30}$

En de tweede manier is om direct de grootte van de vector te berekenen die wordt verkregen bij de vermenigvuldiging:

$\lvert 6\cdot \vv{a} \rvert =\sqrt{18^2+(-24)^2} = \sqrt{900} =\bm{30}$

Zodat bij beide procedures wordt aangetoond dat het resultaat niet afhankelijk is van de methode waarmee de modulus wordt berekend.

Oefening 3

Uit de volgende vector:

$\vv{a}=(4,-1)$

Bereken de volgende bewerkingen algebraïsch:

$2\cdot \vv{a}$

$-3\cdot \vv{a}$

$\displaystyle \frac{1}{2} \cdot \vv{a}$

$4\cdot \vv{a}$

Bepaal vervolgens of de resulterende vectoren dezelfde richting en richting hebben als de originele vector, en rangschik ze van kort naar langst.

zie oplossing

We berekenen eerst de vermenigvuldigingen:

$2\cdot \vv{a}=(2\cdot 4, 2 \cdot (-1)) = (8,-2)$

$-3\cdot \vv{a}=(-3\cdot 4, -3 \cdot (-1)) = (-12,3)$

$\displaystyle \frac{1}{2}\cdot \vv{a}=\left(\frac{1}{2}\cdot 4, \frac{1}{2} \cdot (-1)\right) = \left(2,-\frac{1}{2}\right)$

$4\cdot \vv{a}=(4\cdot 4, 4 \cdot (-1)) = (16,-4)$

Daarom hebben vectoren vermenigvuldigd met positieve getallen dezelfde richting en richting als de originele vector. En vectoren vermenigvuldigd met negatieve getallen hebben dezelfde richting, maar de tegenovergestelde richting van de oorspronkelijke vector.

Vectoren van dezelfde richting en dezelfde richting:

$\displaystyle 2\vv{a}, \ 4\vv{a}$

$\displaystyle \frac{1}{2}\vv{a}$

Vectoren met dezelfde richting maar verschillende betekenis:

$-3\vv{a}$

Ten slotte moeten we de vectoren ordenen op basis van hun lengte, of op equivalente wijze, hun module. De vector met de langste lengte (of grootste module) zal degene zijn die vermenigvuldigd is met een groter getal (in absolute waarde), en de vector met de kortste lengte (of kleinste module) zal degene zijn die vermenigvuldigd is met een kleiner getal. aantal (in absolute waarde). De volgorde van de lengtes is dus:

$\displaystyle \begin{vmatrix} \displaystyle\frac{1}{2}\vv{a}\end{vmatrix} <\lvert 2\vv{a}\rvert < \lvert -3\vv{a}\rvert < \lvert 4\vv{a}\rvert$

Merk op dat de lengte of modulus niet afhankelijk is van het teken van de scalair die wordt vermenigvuldigd, aangezien de richting van de vector zijn modulus niet verandert.