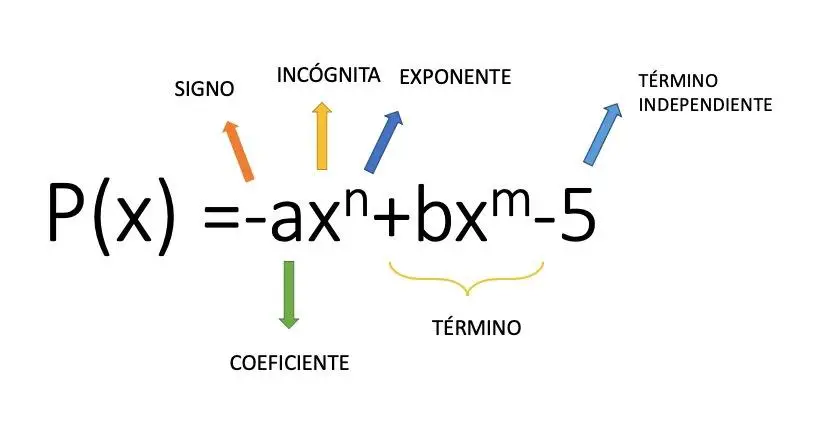
Een monomiaal is een algebraïsche uitdrukking die wordt gevormd door een coëfficiënt (numerieke waarde) die een variabele vermenigvuldigt met een exponent. De uitdrukking 4x² is bijvoorbeeld een monomiaal. Vanuit dit wiskundige concept komen we dus uit bij de polynoom, een reeks optellingen en aftrekkingen van verschillende monomialen. In de afbeelding hierboven zie je een voorbeeld van de structuur van een polynoom dat uit verschillende monomialen bestaat.
soorten polynomen
Via de exponent van een bepaalde monomiaal kunnen we polynomen in verschillende typen indelen. We kunnen deze uitdrukkingen indelen in categorieën zoals: polynoom van de eerste graad, polynoom van de tweede graad, polynoom van de derde graad, enz. Kortom, je moet de monomial identificeren die de grootste exponent heeft en die de graad van de polynoom zal zijn. En als je het eenmaal weet, kun je het indelen in een van de typen waar we het zojuist over hadden.
Polynoom van verschillende variabelen
Bovendien is er ook een andere manier om polynomen te ordenen, namelijk op basis van het aantal monomialen waaruit ze bestaan. Als we bijvoorbeeld een binomiaal hebben, komt dit overeen met het hebben van een polynoom met twee termen, als we een trinominaal hebben, is dit gelijk aan het hebben van een polynoom met drie termen, enz. Al deze manieren om polynomen te catalogiseren hebben oneindig veel subcategorieën. Omdat deze uitdrukkingen kunnen worden samengesteld uit alle gewenste monomieën en ook elke graad kunnen hebben.
Kenmerken en eigenschappen van polynomen
- Absolute graad van een polynoom: In de vorige sectie hebben we de definitie van relatieve graad besproken. Maar in het geval van polynomen die door meer dan één variabele worden gevormd, hebben we de absolute graad die equivalent is aan de maximale som van de exponenten van alle variabelen van deze monomial. In de monomial 5x²y³ is de absolute graad bijvoorbeeld gelijk aan 2 + 3 = 5.
- Geordende polynoom: We definiëren een geordende polynoom met betrekking tot een variabele wanneer de exponenten van die variabele in oplopende of aflopende volgorde zijn gerangschikt. Als we bijvoorbeeld deze polynoom P(x) = 3x + 4x³ – x² vinden, wordt deze in dit geval niet geordend. We moeten dit dus corrigeren en we krijgen dit resultaat: P(x) = 4x³ – x² + 3x.
- Volledige polynoom: Wanneer we een polynoom vinden dat monomialen heeft met alle mogelijke exponenten (van de hoogste graad tot de onafhankelijke term), zeggen we dat het een volledige polynoom is. De volgende uitdrukking: P(x) = 3 x² + 2x – 4 is bijvoorbeeld van dit type omdat er geen ontbrekende exponent tussen 2 en 0 is.
- Homogene polynoom: is die polynoom die in elk van zijn monomialen een gelijke absolute graad heeft. Variabelen kunnen verschillende waarden hebben in de exponent, maar de som van de exponenten van de variabelen in alle monomialen moet noodzakelijkerwijs hetzelfde zijn. Bijvoorbeeld: P(x) = x²y³z + 3 x 4 yz, de twee sommen geven zes 2 + 3 + 1 = 4 + 1 + 1 = 6.
- Identieke polynomen: Wanneer we twee of meer polynomen vinden die de coëfficiënten van dezelfde termen delen, dan zullen we zeggen dat het identieke polynomen zijn. Hieronder zie je een voorbeeld tussen twee polynomen: P(x) = 2x + 27 en Q(x) = 5 (x + 3) – 3 (x – 4), ze zullen identiek zijn omdat ze de coëfficiënten van elke exponent delen : 2x = 5x – 3x en 27 = 15 + 12.
- Nulpolynoom: Deze polynoom heeft alleen nulcoëfficiënten (gelijk aan nul), dus de totale waarde van de polynoom zal ook nul zijn. De polynoom P(x) = 0x³ + 0x² – 0x – 0 is een duidelijk voorbeeld van dit type polynoom, maar moet niet worden verward met Q(x) = 0, omdat je in dit geval een vergelijking vormt en deze niet betekent niet dat alle coëfficiënten van Q(x) 0 zijn.
Numerieke waarde van een polynoom
De numerieke waarde van een polynoom is het resultaat dat we zullen verkrijgen door de variabele van deze uitdrukking te vervangen door een getal. We hoeven deze polynoom eenvoudigweg op te lossen alsof het een gecombineerde bewerking is. Vervolgens leggen we de drie methoden uit die u kunt gebruiken om de numerieke waarde van een uitdrukking als deze te bepalen.
- Directe vervanging: wanneer we direct de waarden krijgen die overeenkomen met elk van de variabelen van de polynoom, vervangen we deze variabelen eenvoudigweg door deze getallen. Op deze manier, als we de polynoom P(x) = 2x² – x + 4 hebben en ons wordt verteld dat x = 3, dan zal de numerieke waarde van de polynoom gelijk zijn aan 2 · 3² – 3 + 4 = 19.
- Variabele resolutie: we zullen dit geval toepassen wanneer ze ons niet direct de waarde van de variabele geven, maar ze geven ons een gelijkwaardigheid. Bijvoorbeeld, P(2) als P(x – 1) = x³ – 2x + 1 waar is, dan zullen we eerst de vergelijking 2 = x – 1 oplossen en x = 3 krijgen. Ten slotte zullen we 3 moeten vervangen door x, zodat 3³ – 2 · 3 + 1 = 22.
- Verandering van variabele: als we een polynoom P(x) = 4x – 2 hebben en we deze waarde willen weten voor P(x + 2). Vervolgens moeten we alle x-en in de uitdrukking veranderen in a(x+2). Dat gezegd hebbende, laten we eens kijken hoe dit laatste opgeloste voorbeeld eruit zou zien: P (x + 2) = 4 (x + 2) – 2.
Bewerkingen met polynomen
Hieronder leggen we uit hoe je de vier basisrekenkundige bewerkingen met polynomen kunt oplossen, waarbij je altijd de hiërarchie van bewerkingen volgt. In elke sectie vindt u een stukje theorie, zodat u weet hoe u in elk geval verder moet gaan, en enkele praktijkvoorbeelden.
toevoeging van polynomen
Om polynomen toe te voegen moeten we rekening houden met het feit dat ze alleen kunnen worden gegroepeerd op vergelijkbare termen , dus als we de polynomen P(x) = 3x³ – x² + 2x – 4 en Q(x) = 2x² + 3x – 2 hebben. Dus om P(x) + Q(x) te maken, zullen we de coëfficiënten van de twee polynomen optellen, vergezeld van dezelfde exponent: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Samenvattend kunnen we zeggen dat we de coëfficiënten van elke vergelijkbare term hebben gegroepeerd en opgeteld en uiteindelijk hebben we alle termen in één polynoom uitgedrukt .
aftrekken van polynomen
Het aftrekken van polynomen wordt op dezelfde manier opgelost als het optellen, het enige verschil is uiteraard het symbool. Vervolgens groeperen we vergelijkbare termen, trekken we ze af en transformeren we ze allemaal in één enkele uitdrukking. Hieronder laten we u een voorbeeld zien: P(x) = 5x³ – 2x² + x – 3 en Q(x) = 3x² + 5x + 4, dan P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.
polynomiale vermenigvuldiging
Bij het oplossen van dit soort vermenigvuldigingen kan het een beetje ingewikkeld worden, maar als je alle stappen volgt die we je vertellen, dan komt alles goed. In deze wiskundige bewerking zullen alle monomialen met alle andere samenwerken, dit betekent dat we niet alleen vergelijkbare termen zullen vermenigvuldigen. Bovendien zullen niet alleen de coëfficiënten veranderen , maar ook de exponenten . Met dit voorbeeld zul je alles veel beter begrijpen: P(x) = 2x² + 3x – 1 en Q(x) = 2x + 3:
P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3
Kortom, we vermenigvuldigen de coëfficiënten van elke term van een polynoom met alle die van de tweede en passen vervolgens de machtseigenschap van a n · a m = a n+m toe.
deling van polynomen
Ten slotte hoeven we alleen maar uit te leggen hoe we de deling van polynomen kunnen oplossen. Eigenlijk moeten we de distributieve eigenschap van deling toepassen: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d). En we zullen ook de volgende machtsverheffingseigenschap toepassen op n ÷ a m = a nm . We zullen dit nu zien met een eenvoudig voorbeeld: P(x) = 3x³ – 6x² + 9x en Q(x) = 3x.
P(x) ÷ Q(x) = ( 3x³ – 6x² +9x ) ÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3
Nu je hebt gezien hoe je al deze bewerkingen met polynomen kunt oplossen, hopen we dat je weet hoe je dit in de praktijk kunt toepassen. Maar als je denkt dat dit niet het geval is en je wilt nog een beetje blijven oefenen, dan raden we je aan om op deze pagina enkele opgeloste oefeningen te bekijken. Deze zullen je helpen bij het internaliseren van al deze wiskundige concepten.
Veeltermen ontbinden in factoren
Om polynomen te ontbinden, kunt u dit handmatig doen, zoals uitgelegd in het artikel in deze laatste link, of u kunt dit doen met behulp van een Ruffini-rekenmachine . We raden aan om het met deze tweede optie te doen als je het snel wilt doen, maar als je net leert factoriseren, kun je beter handmatig oefenen. De manier om dit te doen moet worden gekozen op basis van uw situatie.
Los polynomen op met de wetenschappelijke rekenmachine
Er zijn tegenwoordig veel verschillende wetenschappelijke rekenmachines op de markt. Maar als je op zoek bent naar een goedkope rekenmachine die polynomen kan oplossen , dan raden wij de Casio FX-991SPX II aan. Het is gemakkelijk te gebruiken, zeer krachtig en functioneel, waardoor het perfect is voor elke wiskundestudent op de middelbare en middelbare school. Hieronder leggen we kort uit hoe wiskundige uitdrukkingen van deze stijl worden opgelost met behulp van dit of een vergelijkbaar Casio-model.
U moet eerst de numerieke waarde van de variabelen invoeren, deze schrijven en vervolgens op “STO” + letter van de variabele drukken, bijvoorbeeld x. Dus als alle variabelen zijn gedefinieerd, hoeft u alleen maar de polynomiale uitdrukking te schrijven zoals deze is voor alle variabelen en alle getallen. En ten slotte moet u op de gelijktoets drukken, op deze manier krijgt u het resultaat dat gelijk is aan de numerieke waarde van de polynoom.