Polynomiale functies

In dit artikel vindt u een zeer uitgebreide uitleg over polynomiale functies , aangevuld met voorbeelden. Bovendien zul je kunnen zien hoe polynomiale functies in het dagelijks leven worden gebruikt dankzij de oefeningen die we je aan het einde zullen presenteren.

Wat is een polynomiale functie?

Polynoomfuncties of polynoomfuncties zijn functies die worden gegeven door een algebraïsche uitdrukking die equivalent is aan een polynoom . Dit betekent dat de uitdrukking de structuur van een polynoom moet volgen: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ , afhankelijk van de structuur waarvan we zullen bepaal het type polynoomfunctie dat we gaan verwerken. Een ander zeer relevant kenmerk van deze functies is dat al hun exponenten van de onbekenden positief en gehele getallen zijn.

Delen van een polynomiale functie

We kunnen drie belangrijke elementen met betrekking tot deze functies benadrukken:

• Polynomiale coëfficiënten: dit zijn de getallen die bij de onbekenden horen, de 3 van de volgende term is bijvoorbeeld een coëfficiënt: 3x ² . Opgemerkt moet worden dat er evenveel coëfficiënten zijn als er termen in de polynoom zijn.
• Exponenten of indices van de polynoom: dit zijn de machten van de onbekenden, de 2 van de volgende term is bijvoorbeeld een exponent: 3x ² . En zoals we al hebben uitgelegd, zullen ze in het geval van een polynoomfunctie altijd positief en geheel getal zijn.
• Graad van de polynoom: deze waarde is gelijk aan de exponent van de hoogste graad van alle termen waaruit de polynoom bestaat. In het geval van de polynoom f(x) = 3x ² – 4x + 2 is de graad gelijk aan twee.

Hoe weet je of een functie polynoom is of niet?

Om een polynomiale functie te identificeren, moeten we kijken of deze voldoet aan de kenmerken waar we het zojuist over hadden. We beginnen met te controleren of de uitdrukking die de functie definieert een polynoomstructuur heeft: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ . En dan zullen we controleren of de indices positief en geheel getal zijn. Met deze eenvoudige stappen kunnen we bepalen of een functie polynoom is of niet.

Soorten polynoomfuncties met voorbeelden

Vervolgens laten we u de verschillende soorten polynoomfuncties zien die er bestaan, die worden geclassificeerd op basis van de graad van de polynoom. Daarnaast vindt u voor elk type een grafische voorbeeldweergave. Dankzij deze voorbeelden van polynomiale functies kun je de verschillen tussen de verschillende categorieën beter zien.

constante functies

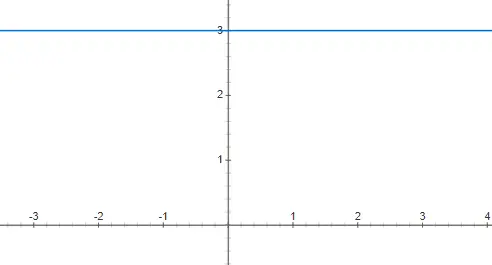
Constante functies zijn equivalent aan een polynoom van graad 0, dit betekent dat de coëfficiënt van x 0 is. Dit is de reden waarom dit soort functies niet afhankelijk zijn van de waarde van de onafhankelijke variabele x. Daarom is de grafische weergave ervan een horizontale lijn, die oneindig is. Hieronder vindt u het voorbeeld f(x) = 3 weergegeven:

polynomiale functies van de eerste graad

Ten tweede vinden we de polynoomfuncties van de eerste graad , die worden gegeven door een polynoom van graad 1 met de volgende structuur: f(x) = mx + n. Deze uitdrukking bestaat uit een getal genaamd helling (m) dat de variabele xy vermenigvuldigt met een constante (n) die aan dit product wordt toegevoegd. Op basis van de waarden van m en n kunnen we dus drie verschillende soorten functies identificeren:

• Affiene functies: dit subtype wordt gekenmerkt door een waarde van n die verschilt van 0, dat wil zeggen dat de waarde van de computer verschilt van 0. Daarom gaat dit type functie niet door het punt (0, 0), ook wel genoemd de oorsprong. Merk ook op dat als m < 0, de functie afnemend zal zijn, terwijl als m > 0, de functie zal toenemen.
• Lineaire functies: Het enige verschil tussen deze functies en affiene functies is dat n = 0, dus ze hebben geen computer. Daarom is de uitdrukking voor lineaire functies equivalent aan f(x) = mx. Dit type is vrij eenvoudig weer te geven, omdat het altijd door het punt (0, 0) gaat en we uit de helling al de grafiek verkrijgen.
• Identiteitsfuncties: dit laatste type is een subgroep van lineaire functies, namelijk an = 0 en m = 1. Dit betekent dat de uitdrukking f(x) = x blijft, waarbij de grafische weergave een diagonaal is die een hoek van 45º vormt met een van de assen. Dit type functie gaat ook door het oorsprongspunt (0, 0).

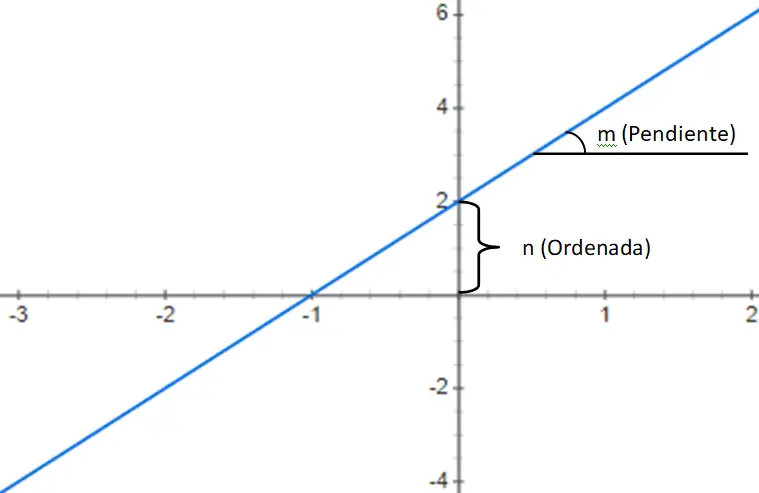
Hieronder vindt u een voorbeeld van een polynoomfunctie van de eerste graad, meer bepaald een affiene functie f(x) = 3x + 2:

kwadratische functies

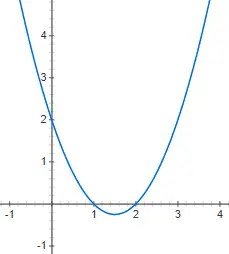
Kwadratische functies of kwadratische functies worden uitgedrukt met behulp van kwadratische polynomen, die de structuur volgen: f(x) = ax ² + bx + c, waarbij a verschillend is van 0. In dit geval is de grafische weergave veel complexer, aangezien deze niet langer een rechte lijn, maar een verticale parabool . Hieronder vind je de weergave van de kwadratische functie f(x) = 2x ² + 4x – 1:

kubieke functies

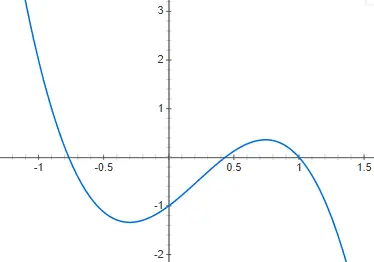
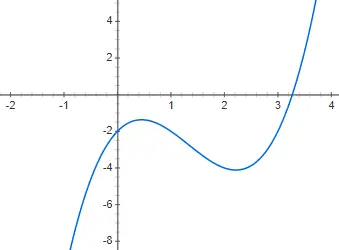
Kubieke functies of functies van de derde graad worden gegeven door een polynoom van graad drie: f(x) = ax ³ + bx ² + cx + d, verschillend van 0. De weergave van een functie van deze stijl is zelfs nog complexer dan die van de tweede graad, omdat het verschillende vormen kan hebben. Hoewel de basisvorm, of in ieder geval de meest voorkomende, degene is die we je in het volgende voorbeeld laten zien, f(x) = 2x ³ – 4x ² + 2x – 2:

Eigenschappen van polynomiale functies

Polynomiale functies hebben een reeks eigenschappen of kenmerken die ze onderscheiden van andere functies, en we zullen ze hieronder zo duidelijk mogelijk beschrijven. Op deze manier, als u dergelijke functies ziet, kunt u ze heel gemakkelijk identificeren:

• Het domein van een polynoomfunctie is gelijk aan alle reële getallen : Dom f = R of Dom f = (-∞, ∞), ze zijn dus continu over de hele reeks reële getallen.
• Het snijpunt op de Y-as is gelijk aan (0, a ₀ ), waarbij ₀ de onafhankelijke term is.
• Snijdt langs de X-as een aantal keren gelijk aan of kleiner dan de graad van de polynoom.
• Polynomiale functies hebben geen asymptoten.
• Als de exponent van alle termen oneven is, is de grafiek symmetrisch rond de coördinaatoorsprong, terwijl als de exponent van alle termen even is, deze symmetrisch is rond de OY-as.
• Het aantal buigpunten van een functie van deze stijl is gelijk aan of kleiner dan n – 2, waarbij n de graad is.
• Het aantal relatieve maxima en minima van een functie van deze stijl is gelijk aan of kleiner dan n – 1, waarbij n de graad is.

Hoe analyseer je een polynomiale functie?

Om een polynomiale functie te analyseren, moeten we dezelfde procedure volgen die we zouden gebruiken om elke andere functie te analyseren. In de volgende lijst hebben we de verschillende elementen samengevat die moeten worden bestudeerd of behandeld:

• Domein en bereik
• Snijpunten met de horizontale en verticale as
• Eentonigheid (toenemend en afnemend, maxima en minima)
• Kromming (in functies van graad groter dan één)

Uiteraard kunnen we de analyse naar een ander niveau tillen en veel andere elementen bestuderen, hoewel dit voldoende zou moeten zijn. Omdat u deze elementen kent, heeft u een duidelijk idee van hoe de functie eruit ziet en kunt u deze grafisch weergeven.

Oefeningen over polynomiale functies

Vervolgens bieden we u een reeks oefeningen aan om te oefenen met het weergeven van functies , in het bijzonder polynomiale functies. Op deze manier consolideert u alle concepten die in dit artikel worden uitgelegd:

Oefening 1

Teken de volgende eerstegraads polynoomfunctie f(x) = x + 2 en zeg welk type het is:

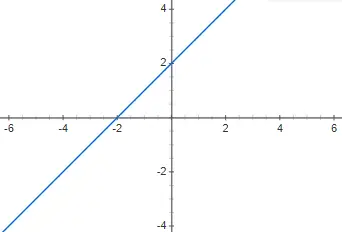
Het is een affiene polynoomfunctie van de eerste graad, omdat deze verschillend is van 0 en m verschillend is van 0.

Oefening 2

Teken de volgende kwadratische polynoomfunctie f(x) = x ² + x – 2:

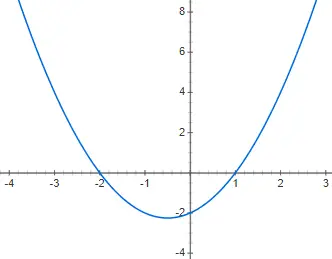
Oefening 3

Grafiek van de volgende derdegraads polynoomfunctie f(x) = x ² + x – 2: