Parallelle vlakken

Op deze pagina vind je alles over evenwijdige vlakken: wanneer twee vlakken evenwijdig zijn, de vergelijkingen van twee evenwijdige vlakken, voorbeelden, opgeloste oefeningen, eigenschappen,…

Wat zijn twee evenwijdige vlakken?

In de analytische meetkunde zijn twee vlakken evenwijdig als ze altijd op dezelfde afstand van elkaar liggen. Daarom snijden twee evenwijdige vlakken elkaar nooit en hebben ze niets met elkaar gemeen.

Twee evenwijdig geplaatste vlakken zijn niet de enige mogelijke relatieve positie tussen vlakken, aangezien twee vlakken in de ruimte (in R3) ook elkaar kunnen snijden of samenvallen.

Hoe weet je of twee vlakken evenwijdig zijn?

Laten we, nadat we de definitie van evenwijdige vlakken hebben gezien, kijken hoe je kunt bepalen of twee vlakken evenwijdig zijn of niet.

Uitgaande van de algemene (of impliciete) vergelijking van twee verschillende plannen:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

De 2 vlakken zullen evenwijdig zijn als hun coëfficiënten A, B en C evenredig zijn met elkaar en niet met de coëfficiënt D. Met andere woorden: parallellisme tussen twee vlakken treedt op als aan de volgende vergelijking is voldaan:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Voorbeeld van twee evenwijdige vlakken

De volgende twee vlakken zijn bijvoorbeeld evenwijdig:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

De plannen zijn parallel omdat de coëfficiënten van de variabelen X, Y, Z evenredig zijn aan elkaar, maar niet aan de onafhankelijke termen:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Bereken de afstand tussen twee evenwijdige vlakken

Twee evenwijdige vlakken bevinden zich altijd op dezelfde afstand. Om de afstand tussen twee evenwijdige vlakken te vinden, kunnen we dus een punt op een van de twee vlakken nemen en de afstand vanaf dat punt tot het andere vlak berekenen. Om de afstand tussen 2 evenwijdige vlakken te berekenen, is het daarom noodzakelijk om de formule voor de afstand van een punt tot een vlak te kennen.

Het is een methode om de afstand tussen twee parallelle vlakken te vinden. Er is echter een nog eenvoudiger manier om dit te doen wanneer de coëfficiënten A, B en C van de vergelijkingen van de twee vlakken samenvallen:

Beschouw de algemene (of impliciete) vergelijkingen van twee parallelle vlakken:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

De formule voor het berekenen van de afstand tussen twee evenwijdige vlakken is:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

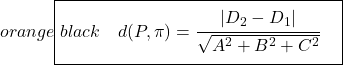
Het is dus zeker gemakkelijker om de afstand tussen twee parallelle vlakken te vinden met behulp van de formule, omdat het gewoon een kwestie is van het toepassen van de formule en dat is alles, maar het hangt af van het probleem. Bovendien denken we dat het het beste is om beide manieren om afstand te berekenen uit te leggen, zodat u degene kunt kiezen die u verkiest.

Voorbeeld van het berekenen van de afstand tussen twee evenwijdige vlakken

Als voorbeeld berekenen we de afstand tussen de volgende twee vlakken:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

We moeten eerst verifiëren dat we te maken hebben met twee evenwijdige vlakken. Alle coëfficiënten van de vlakvergelijkingen zijn dus proportioneel, behalve de onafhankelijke termen, dus het zijn in feite twee parallelle vlakken.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In dit geval vallen de termen A, B en C van de vergelijkingen van de twee vlakken niet samen, maar we kunnen dit bereiken door de gehele vergelijking van het tweede vlak door twee te delen:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

De vergelijkingen van de twee vlakken hebben nu dus dezelfde coëfficiënten A, B en C. Daarom kunnen we eenvoudig de afstand tussen de twee vlakken berekenen met de formule voor de afstand tussen twee evenwijdige vlakken:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

We vervangen de waarden en lossen de bewerkingen op:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Zodat de afstand tussen het ene vlak en het andere vlak gelijk is aan één.

Eigenschappen van parallelle vlakken

De kenmerken van evenwijdige vlakken zijn als volgt:

Reflexieve eigenschap : elk vlak is evenwijdig aan zichzelf.

$\pi_1 \parallel \pi_1$

Symmetrische eigenschap : Als het ene vlak evenwijdig is aan het andere, is dit vlak ook evenwijdig aan het eerste. Deze eigenschap wordt ook bezeten door loodrechte vlakken.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Transitieve eigenschap : als een vlak evenwijdig is aan een ander vlak, en dit tweede vlak is evenwijdig aan een derde vlak, dan is het eerste vlak ook evenwijdig aan het derde vlak.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$