Parabool (wiskunde): definitie, vergelijking, elementen, voorbeelden,…

Op deze pagina vind je alles over de parabool: wat het is, wat het vertegenwoordigt, de elementen (focus, richtlijn, hoekpunt, enz.) de vergelijking (met de verschillende soorten vergelijkingen van de parabool), voorbeelden, opgeloste oefeningen, zijn eigenschappen, zijn toepassingen,…

Wat is een gelijkenis?

De parabool is een concept dat heel verschillende betekenissen heeft, maar de wiskundige definitie ervan is als volgt:

In de wiskunde is een parabool de verzameling punten op het vlak die op gelijke afstand liggen van een vast punt (het brandpunt genoemd) en een vaste lijn (de richtlijn genoemd).

Daarom bevindt elk punt in een parabool zich op dezelfde afstand van het brandpunt en de richtlijn.

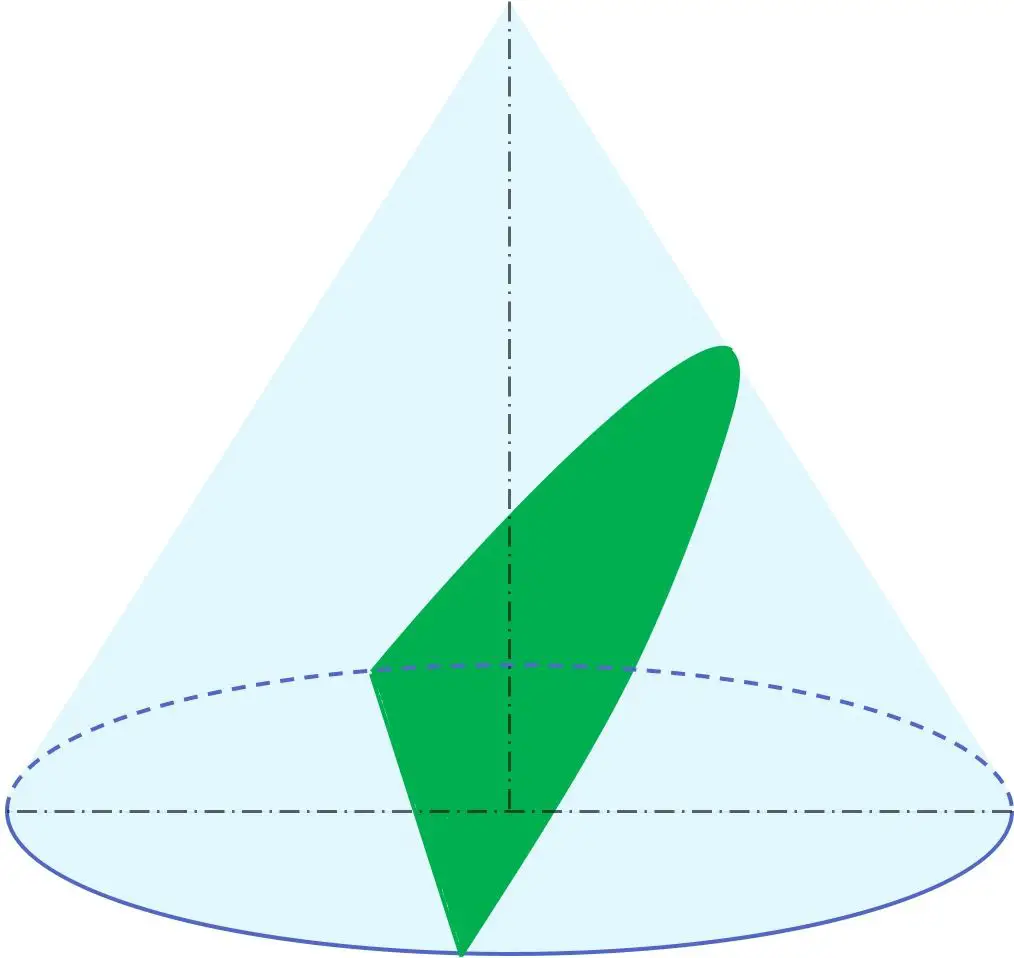
Bovendien is parabool in de geometrie een van de kegelsneden, samen met de omtrek, ellips en hyperbool. Met andere woorden: een parabool kan worden verkregen uit een kegel.

In het bijzonder vloeit de parabool voort uit de doorsnede van een kegel door een vlak met een hellingshoek ten opzichte van de omwentelingsas die equivalent is aan de hoek van de generator van de kegel. Daarom is het vlak dat de parabool bevat evenwijdig aan de generator van de kegel.

Elementen van een parabool

De kenmerken van een parabool zijn afhankelijk van de volgende elementen:

Focus (F) : is een vast punt binnen de parabool. De afstand van elk punt van de parabool tot het brandpunt is gelijk aan de afstand van hetzelfde punt tot de richtlijn van de parabool.
Directix (D) : het is een vaste lijn buiten de parabool. Een punt van de parabool bevindt zich op dezelfde afstand van de richtlijn als van het brandpunt van de parabool.
Parameter (p) : is de afstand van de focus tot de regisseur.
Straalvector (R) : is het segment dat een punt van de parabool met het brandpunt verbindt. De waarde ervan valt samen met de afstand van het punt tot de richtlijn.
As (E) : is de lijn loodrecht op de richtlijn die door het brandpunt gaat en de symmetrieas van de parabool is, in de onderstaande grafiek komt deze overeen met de computeras (Y-as). Ook wel brandpuntsas genoemd.
Vertex (V) : is het snijpunt tussen de parabool en zijn as.
Brandpuntsafstand : is de afstand tussen het brandpunt en het hoekpunt, of tussen de richtlijn en het hoekpunt. De waarde ervan is altijd gelijk aan
$\displaystyle \frac{p}{2}.$

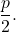
rechter zijde

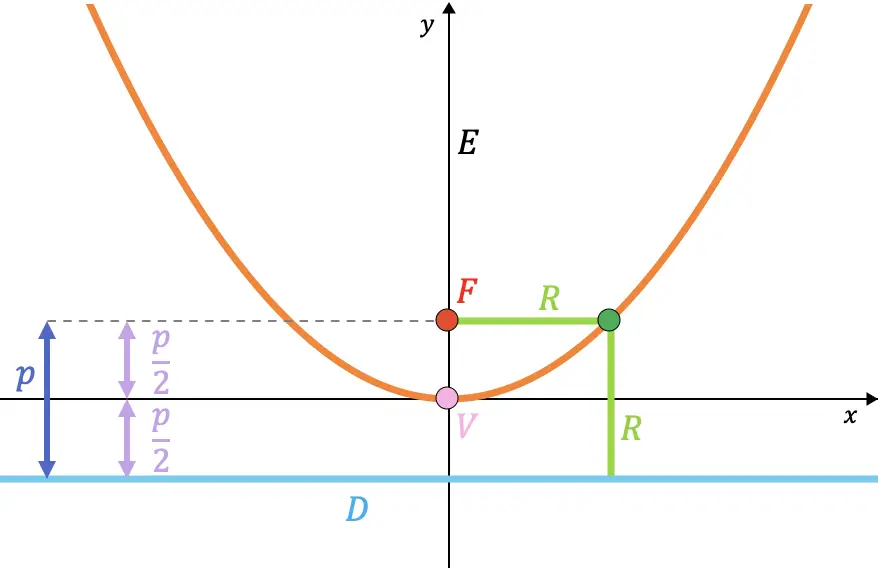
De rechterkant van een parabool is het akkoord binnen de parabool dat door het brandpunt gaat en evenwijdig is aan de richtlijn.

Op dezelfde manier kan worden aangetoond dat de lengte van de rechterkant altijd tweemaal de waarde van de parameter is

$p.$

$\lvert LL'\rvert = 2p$

Aan de andere kant vormen de twee lijnen die de parabool raken en door de uiteinden van de rechterkant gaan, een hoek van 45 graden met de rechterkant zelf en snijden ze elkaar ook aan de bovenkant van de parabool.

paraboolvergelijkingen

De vergelijking van een parabool is een soort kwadratische functie omdat deze altijd minimaal 1 kwadraatterm moet hebben. Bovendien hangt de vergelijking van een parabool af van de horizontale of verticale oriëntatie.

In de analytische meetkunde zijn er dus verschillende manieren om een parabool wiskundig uit te drukken: de canonieke of gereduceerde vergelijking , de gewone vergelijking en de algemene vergelijking van de parabool.

Gereduceerde of canonieke vergelijking van de parabool

Wat de gereduceerde of canonieke vergelijking onderscheidt van andere paraboolvergelijkingen is dat het hoekpunt van de parabool de oorsprong is van de coördinaten , dat wil zeggen het punt (0,0).

De vorm van de gereduceerde vergelijking van de parabool hangt af van het feit of deze horizontaal of verticaal is. Bekijk de volgende grafische weergave waarin de 4 mogelijke varianten zijn aangegeven:

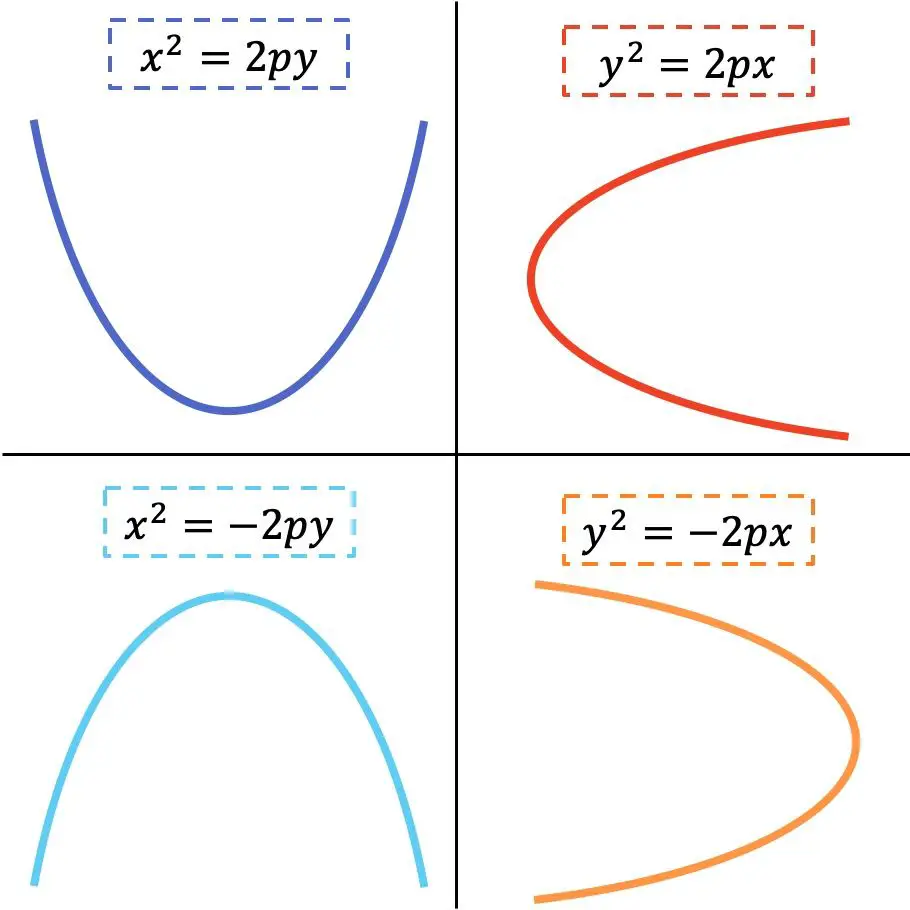
Goud

$p$

is de karakteristieke parameter van de parabool.

Zoals je in de vorige afbeelding kunt zien, is de parabool verticaal als de variabele x vierkant is, en als de variabele y kwadraat is, is de parabool horizontaal. Aan de andere kant hangt de richting van de takken van de parabool af van het teken van de vergelijking.

Gewone vergelijking van de parabool

We hebben zojuist gezien hoe de vergelijking van de parabool eruit ziet als het hoekpunt of middelpunt ervan overeenkomt met de oorsprong van de coördinaten (de gereduceerde of canonieke vergelijking), maar wat is de vergelijking van de parabool als het hoekpunt buiten de ‘oorsprong’ ligt?

Wanneer het hoekpunt van de parabool een willekeurig punt is, gebruiken we de gewone vergelijking van de parabool , waarvan de uitdrukking is:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

waarbij het middelpunt of de top van de parabool het punt is

$V(x_0,y_0).$

De vorige vergelijking komt overeen met de verticaal georiënteerde parabool, dat wil zeggen dat de brandpuntsas van de parabool evenwijdig is aan de Y-as.

Op dezelfde manier moeten we, om een horizontaal georiënteerde parabool te definiëren (de brandpuntsas is evenwijdig aan de X-as), de volgende variant van de gewone vergelijking van de parabool gebruiken:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Waar, zoals voorheen, het middelpunt of de top van de parabool het punt is

$V(x_0,y_0).$

Algemene vergelijking van de parabool

Tot nu toe worden alle paraboolvergelijkingen die we hebben geanalyseerd gebruikt om horizontale of verticale parabolen uit te drukken. Maar uiteraard kan een parabool ook schuin of hellend zijn .

Om dit type parabool uit te drukken, gebruiken we de algemene paraboolvergelijking , waarvan de formule als volgt is:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

De bovenstaande vergelijking is een parabool als en slechts als de coëfficiënten

$A$

$C$

zijn niet tegelijkertijd nul en bovendien is aan de volgende voorwaarde voldaan:

$B^2-4AC =0$

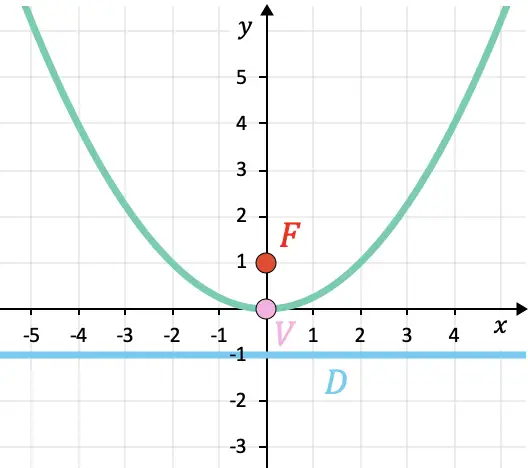
Voorbeeld van hoe u het hoekpunt, het brandpunt en de richtlijn van een parabool uit de vergelijking kunt vinden

Bij veel parabooloefeningen en -problemen wordt u gevraagd het hoekpunt, het brandpunt en de richtlijn van een bepaalde parabool te berekenen. Laten we daarom eens kijken hoe dit wordt gedaan aan de hand van een voorbeeld:

Zoek het hoekpunt, het brandpunt en de richtlijn van de volgende parabool:

$x^2 = 4y$

Het fundamentele ding om dit type paraboolprobleem op te lossen is het bepalen van de parameter p van de parabool . In dit geval komt de vergelijking van de parabool overeen met de gereduceerde of canonieke vergelijking (verticale parabool):

$x^2 = 2py$

Daarom is de parameter p :

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

Aan de andere kant, aangezien de parabool de gereduceerde of canonieke vergelijking volgt, betekent dit dat het hoekpunt of middelpunt zich aan de oorsprong van de coördinaten bevindt:

$\bm{V(0,0)}$

Zodra we het hoekpunt en de parameterwaarde van de parabool kennen, kunnen we gemakkelijk het brandpunt en de richtlijn ervan vinden.

De kwadratische term van de vergelijking is de variabele x , zodat de as van de parabool evenwijdig zal zijn aan de as OY en, omdat het hoekpunt het punt (0,0) is, de as van de parabool de OY zal zijn. as zelf. Het brandpunt van een parabool bevindt zich dan altijd op de as van de parabool en op een afstand van

$p/2$

vanaf de top van de parabool, dus de coördinaten zijn:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Op dezelfde manier zal de richtlijn de horizontale lijn zijn die zich op een afstand bevindt

$p/2$

vanaf het hoekpunt van de parabool, wat de oorsprong is van de coördinaten. De vergelijking van de lijn zal daarom zijn:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

De parabool is hieronder weergegeven, zodat u de resultaten kunt controleren:

opgeloste paraboolvergelijkingsoefeningen

Eigenschappen van parabolen

Alle parabolen hebben de volgende eigenschappen:

Een parabool is een open curve, of met andere woorden, hij bestaat uit twee takken zonder gemeenschappelijke punten die zich onbeperkt uitstrekken.
Elke parabool heeft een unieke symmetrieas, waar het hoekpunt van de parabool zich bevindt.
Een verticaal georiënteerde parabool is convex als de takken omhoog gaan; integendeel, de parabool is hol als zijn takken naar beneden gaan.
De excentriciteit van een parabool is gelijk aan eenheid (1). De excentriciteit is een coëfficiënt die in dit geval wordt berekend door de afstand van het brandpunt tot het midden van de parabool te delen door de afstand van het hoekpunt tot de richtlijn (en de twee afstanden vallen altijd samen in hun waarde).
Uit de vorige eigenschap volgt dat alle parabolen gelijksoortig of soortgelijk zijn.
Een parabool heeft geen asymptoten.

parabolische toepassingen

Nu je goed bekend bent met de betekenis van een gelijkenis, vraag je je misschien af: wat is het nut van een gelijkenis?

Nou ja, ook al lijkt het je niet zo, de geometrische vorm van een parabool is in het echte leven heel gebruikelijk. Bij het gooien van een bal maakt deze bijvoorbeeld vaak een parabolische beweging, vooral bij basketbal. Welnu, de paraboolvergelijking is erg handig voor het analytisch bestuderen van het parabolische pad dat de bal volgt.

Een andere toepassing van de schotel betreft antennes (vandaar de naam paraboolantenne). Omdat elke straal die op een object met een parabolische vorm valt, evenwijdig aan de symmetrieas, rechtstreeks naar het brandpunt wordt gereflecteerd, worden alle stralen die naar de paraboolantenne gaan, geconcentreerd in het brandpunt en dit kan op verschillende manieren worden gebruikt. Daarom is de focus van een gelijkenis zo belangrijk.

Problemen met de schotel opgelost

Oefening 1

Bereken het hoekpunt, het brandpunt en de richtlijn van de parabool waarvan de vergelijking als volgt is:

$y^2 = 8x$

zie oplossing

Ten eerste zal de parabool horizontaal zijn omdat deze de volgende uitdrukking volgt van de gereduceerde of canonieke vergelijking van de parabool:

$y^2 = 2px$

De parameter p is dus:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

Aan de andere kant, aangezien de parabool de gereduceerde of canonieke vergelijking volgt, betekent dit dat het hoekpunt of middelpunt zich aan de oorsprong van de coördinaten bevindt:

$\bm{V(0,0)}$

Zodra we het hoekpunt en de parameterwaarde van de parabool kennen, kunnen we eenvoudig de focus en richtlijn berekenen.

De kwadratische term van de vergelijking is de variabele en dat wil zeggen dat de as van de parabool evenwijdig zal zijn aan de OX-as en, aangezien het hoekpunt het punt (0,0) is, zal de as van de parabool in feite zijn de OX-as zelf. Het brandpunt van een parabool bevindt zich dan altijd op de as van de parabool en op een afstand van

$p/2$

vanaf de top van de parabool, waarvan de coördinaten zijn:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Ook de richtlijn bevindt zich op afstand

$p/2$

vanaf de top van de parabool, die de oorsprong is van de coördinaten en loodrecht staat op de brandpuntsas. De vergelijking van de richtlijn is daarom:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Oefening 2

Zoek het hoekpunt, het brandpunt en de richtlijn van de parabool waarvan de vergelijking als volgt is:

$(x-4)^2 = -16(y+1)$

zie oplossing

De parabool wordt gedefinieerd volgens de gewone vergelijking (as evenwijdig aan de Y-as), waarvan de formule is:

$(x-x_0 )^2 = 2p (y-y_0)$

De parameter p is dus:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

Aan de andere kant impliceert de gewone vergelijking van de parabool in dit geval dat het middelpunt ervan niet de oorsprong van de coördinaten is. Aan de andere kant zijn de cartesiaanse coördinaten van het hoekpunt van de parabool de getallen tussen haakjes met een veranderd teken. :

$\bm{V(4,-1)}$

Zodra we het hoekpunt en de parameterwaarde van de parabool kennen, kunnen we de focus en richtlijn berekenen.

De kwadratische term van de vergelijking is de variabele x , zodat de as van de parabool evenwijdig is aan de as OY. Het brandpunt van een parabool bevindt zich dus altijd op de as van de parabool en op een afstand van

$p/2$

vanaf het hoekpunt van de parabool, zodat de coördinaten van het brandpunt die van het hoekpunt zijn door optelling

$p/2$

verticaal:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Op dezelfde manier zal de richtlijn de horizontale lijn zijn die zich op een afstand bevindt

$p/2$

vanaf de top van de parabool. De vergelijking van de richtlijn is daarom:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Oefening 3

Bepaal de parabolische vergelijking waarvan de as evenwijdig is aan de abscis-as, het punt V(5,2) als hoekpunt heeft en het brandpunt het punt P(8,2) is.

zie oplossing

In dit geval is het hoekpunt van de parabool niet de oorsprong van de coördinaten, dus hebben we de gewone vergelijking nodig om de parabool van de uitspraak te definiëren. Bovendien is de brandpuntsas van de parabool evenwijdig aan de x-as, wat betekent dat de parabool horizontaal georiënteerd zal zijn (de takken zullen naar rechts of naar links gaan) en daarom moet de kwadratische term van de vergelijking de variabele zijn j :

$(y-y_0 )^2 = 2p (x-x_0)$