Hier leggen we uit hoe functie-optimalisatieproblemen stapsgewijs worden opgelost. Daarnaast kun je oefenen met oefeningen die zijn opgelost op optimalisatieproblemen.
Wat zijn optimalisatieproblemen?
Optimalisatieproblemen zijn problemen waarbij men het maximum of minimum van een functie moet vinden. Een optimalisatieprobleem zou bijvoorbeeld betrekking hebben op het berekenen van het maximum van een functie die de winst van een bedrijf definieert.
Hoe optimalisatieproblemen op te lossen
Stappen om problemen met functie-optimalisatie op te lossen:
- Stel de functie in die moet worden geoptimaliseerd.
- Leid de te optimaliseren functie af.
- Vind de kritieke punten van de functie die moet worden geoptimaliseerd. Om dit te doen, moet u de afgeleide van de functie gelijk stellen aan nul en de resulterende vergelijking oplossen.
- Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Voorbeeld van een optimalisatieprobleem
Gezien de theorie van optimalisatieproblemen, zullen we een dergelijk probleem stap voor stap oplossen, zodat u kunt zien hoe ze worden uitgevoerd.
- Bereken van alle rechthoekige driehoeken waarvan de poten in totaal 10 cm zijn, de afmetingen van de driehoek met de maximale oppervlakte.
Om het probleem op te lossen, noemen we de ene tak van de driehoek x en de andere tak y :

Stap 1: Stel de te optimaliseren functie in.
We willen dat de oppervlakte van de driehoek maximaal is, en de formule voor de oppervlakte van een driehoek is:
![]()
In ons geval is de basis van de driehoek x en de hoogte y . Nog:
![]()
We hebben al de functie om te optimaliseren, maar deze hangt af van twee variabelen, terwijl deze slechts van één kan afhangen. De verklaring vertelt ons echter dat de twee poten in totaal 10 cm moeten zijn. Nog:
![]()
We lossen y op uit deze vergelijking:
![]()
En we vervangen de uitdrukking door de functie:
![]()
![]()
We hebben nu de geplande optimalisatiefunctie en deze is slechts afhankelijk van één variabele, dus we kunnen doorgaan naar de volgende stap.
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
Het is een rationale functie, dus passen we de formule voor de afgeleide van deling toe om deze af te leiden:
![]()
![]()
Stap 3: Zoek de kritieke punten.
Om de kritische punten van de functie te vinden, moeten we de afgeleide gelijk stellen aan nul en de resulterende vergelijking oplossen:
![]()
![]()
De 4 deelt de hele linkerkant, dus we kunnen deze vermenigvuldigen door de hele rechterkant te vermenigvuldigen:
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Om de monotonie van de functie te bestuderen, vertegenwoordigen we het kritieke punt aan de rechterkant:
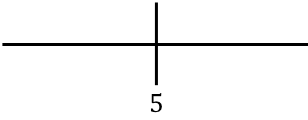
En nu evalueren we het teken van de afgeleide in elk interval om erachter te komen of de functie stijgend of dalend is. Om dit te doen, nemen we een punt in elk interval (nooit het kritieke punt) en kijken we welk teken de afgeleide op dat punt heeft:
![]()
![]()
![]()
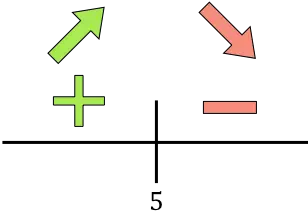
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de intervallen voor het verhogen en verlagen van de functie:
Groei:
![]()
Afname:
![]()
Bij x=5 gaat de functie van stijgend naar dalend, dus x=5 is een relatief maximum van de te optimaliseren functie .
Daarom is x=5 de waarde van de tak van de driehoek die de maximale oppervlakte heeft. Bereken eenvoudig de waarde van het andere been:
![]()
Concluderend zijn de waarden die het maximale oppervlak van de driehoek maximaliseren:
![]()
![]()
Optimalisatieproblemen opgelost
Probleem 1
Het geneesmiddel wordt aan een zieke persoon gegeven en
![]()
een paar uur later wordt de bloedconcentratie van het actieve ingrediënt gegeven door de functie
![]()
milligram per milliliter. Bepaal de maximale waarde van
![]()
en geeft aan wanneer genoemde waarde wordt bereikt.
Stap 1: Stel de te optimaliseren functie in.
In dit probleem geven ze ons al de voorgestelde functie, namelijk
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
De functie is samengesteld uit het product van 2 functies. Om de afgeleide van de functie te berekenen, moeten we daarom de regel voor de afgeleide van een product toepassen:
![]()
![]()
Stap 3: Zoek de kritieke punten.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
We nemen de gemeenschappelijke factor om de vergelijking op te lossen:
![]()
Om de vermenigvuldiging gelijk te maken aan 0, moet een van de twee elementen van de vermenigvuldiging nul zijn. Daarom stellen we elke factor gelijk aan 0:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Een getal dat is verhoogd naar een ander getal kan nooit 0 opleveren, daarom
![]()
Er is geen oplossing.
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Om de monotonie van de functie te bestuderen, vertegenwoordigen we het kritieke punt aan de rechterkant:
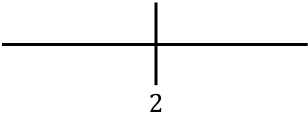
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
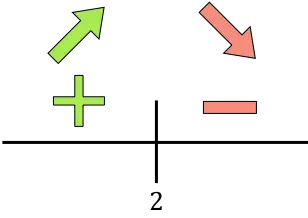
Als de afgeleide positief is, betekent dit dat de functie toeneemt, maar als de afgeleide negatief is, betekent dit dat de functie afneemt. De intervallen van groei en afname van de te optimaliseren functie zijn dus:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend op t=2, dus t=2 is een maximum van de functie. De maximale concentratie zal dus over t=2 uur worden bereikt.
Ten slotte vervangen we de waarde waarbij het maximum optreedt in de oorspronkelijke functie om de waarde van de maximale concentratie te vinden:
![]()
Probleem 2
Eén winkel hoopt 40 elektrische scooters te verkopen tegen een prijs van € 1.000 per scooter. Maar volgens marktonderzoek zal er voor elke € 50 korting op de scooterprijs een stijging in de verkoop van de top 10 best verkochte scooters plaatsvinden.
Schrijf eerst de omzetfunctie van de winkel op basis van het aantal keren dat de oorspronkelijke prijs van € 1.000,- voor de scooter met € 50,- is verlaagd. Bepaal vervolgens de prijs van de scooter om maximale winst te behalen en de inkomsten die voor die prijs worden verdiend.
Stap 1: Stel de te optimaliseren functie in.
De probleemstelling geeft ons een idee, omdat deze ons vertelt dat de functie afhankelijk moet zijn van het aantal keren dat de initiële prijs met $ 50 wordt verlaagd. We noemen daarom x het aantal keren dat de prijs met € 50 wordt verlaagd:
![]()
€
De opbrengstfunctie is het aantal verkochte scooters vermenigvuldigd met de prijs van elke scooter:
![]()
Het aantal verkochte scooters bedraagt 40 plus 10 scooters voor elke prijsverlaging van € 50. Nog:
![]()
De prijs van elke scooter bedraagt bij aanvang € 1000,- en daalt met € 50,- bij elke prijsdaling. Nog:
![]()
De functie om het probleem te optimaliseren is daarom:
![]()
![]()
![]()
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
Omdat het een polynomiale functie is, is de afgeleide gemakkelijker te berekenen:
![]()
Stap 3: Zoek de kritieke punten van de functie.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Om de monotoniciteit van de functie te bestuderen, vertegenwoordigen we het kritieke punt berekend op de getallenlijn:
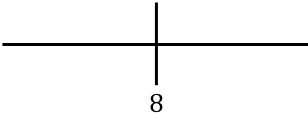
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
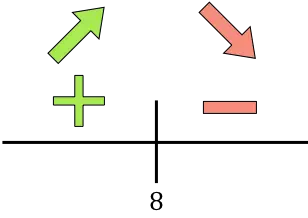
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij x=8, dus x=8 is een maximum van de functie. Het maximale inkomen wordt dus verkregen door 8 maal de korting van € 50,-.
We vervangen nu de waarde waarbij het maximale inkomen verschijnt in de oorspronkelijke functie, om de waarde van het maximale inkomen te vinden:
![]()
![]()
€
En de prijs van elke scooter na 8 keer € 50 korting te hebben gemaakt, is:
![]()
![]()
€
Probleem 3
De kostenfunctie (in duizenden euro’s) van een bedrijf kan worden bepaald met behulp van de volgende uitdrukking:
![]()
Goud
![]()
vertegenwoordigt de duizenden geproduceerde eenheden van een bepaald item.
Bepaal hoeveel er moet worden geproduceerd zodat de kosten minimaal zijn, wat die kosten zijn en wat de kosten zouden zijn als geen van deze items zou worden geproduceerd.
Stap 1: Stel de te optimaliseren functie in.
De probleemstelling biedt ons al de te optimaliseren functie, namelijk
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
![]()
Stap 3: Zoek de kritieke punten.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Wij vertegenwoordigen het kritieke punt aan de rechterkant:
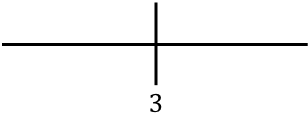
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
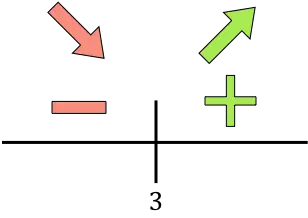
Als de afgeleide groter is dan nul, neemt de functie over dit interval toe. Aan de andere kant, als de afgeleide kleiner is dan nul, neemt de functie in dit interval af. De intervallen van toename en afname van de functie zijn dus:
Groei:
![]()
Afname:
![]()
De functie gaat van afnemend naar toenemend bij x=3, dus x=3 is een minimum van de functie. Daarom zullen de minimale kosten worden bereikt door 3.000 eenheden te produceren.
We vervangen nu de waarde waarbij de minimale kosten worden bereikt in de oorspronkelijke functie om de minimale kostenwaarde te vinden:
![]()
miljoenen euro’s.
Aan de andere kant vragen ze ons wat de kosten zouden zijn als er niets geproduceerd zou worden, dat wil zeggen wanneer
![]()
Het is daarom noodzakelijk om te berekenen
![]()
![]()
miljoenen euro’s.
Probleem 4
We willen een rechthoekig houten frame bouwen dat een oppervlakte van 2 m 2 begrenst. We weten dat de prijs van hout € 7,5/m bedraagt voor horizontale zijden en € 12,5/m voor verticale zijden. Bepaal de afmetingen die de rechthoek moet hebben zodat de totale kosten van het frame zo laag mogelijk zijn en deze kosten minimaal zijn.
Stap 1: Stel de te optimaliseren functie in.
Om het probleem op te lossen, noemen we de horizontale zijde x en de verticale zijde y :

De aanschaf van een horizontale zijde kost €7,5 en de aanschaf van een verticale zijde kost €12,5. Bovendien hebben we voor elk frame twee horizontale zijden en twee verticale zijden nodig. Daarom kunnen de kosten van het frame worden bepaald met de volgende functie:
![]()
We hebben al de functie om te optimaliseren. Maar het hangt af van twee variabelen, terwijl het slechts van één kan afhangen. De verklaring vertelt ons echter dat de oppervlakte van het frame 2 m2 moet zijn. Nog:
![]()
We verwijderen de variabele y :
![]()
En we vervangen de uitdrukking gevonden in de te optimaliseren functie:
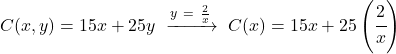
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
![]()
Stap 3: Zoek de kritieke punten.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
![]()
![]()
![]()
We vermenigvuldigen transversaal om de vergelijking met breuken op te lossen:
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
We vertegenwoordigen het kritieke punt dat is gevonden om de monotonie van de functie op de lijn te analyseren:
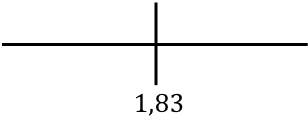
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
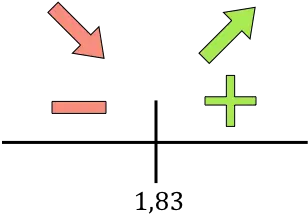
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
De functie verandert van afnemend naar toenemend bij x=1,83, dus x=1,83 is een minimum van de functie.
Daarom is x=1,83 de waarde van de horizontale zijde die de minimale kosten vertegenwoordigt. Laten we nu de waarde van de verticale zijde berekenen:
![]()
De waarden waaruit de minimale raamwerkkosten bestaan, zijn dus:
horizontale kant
![]()
verticale kant
![]()
En de minimale kosten die met deze waarden worden bereikt, zijn:
![]()
€
Probleem 5
De deur van een kathedraal wordt gevormd door een halfronde boog die wordt ondersteund door twee kolommen, zoals weergegeven in de volgende afbeelding:
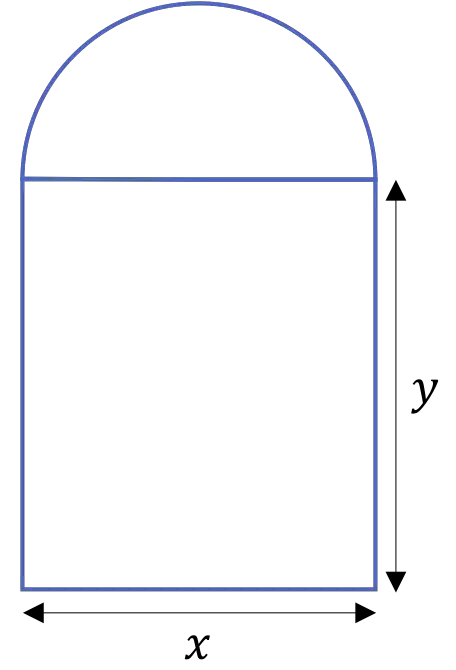
Als de omtrek van de deur 20 m bedraagt, bepaal dan de afmetingen
![]()
En
![]()
waardoor het oppervlak van de gehele deur wordt gemaximaliseerd.
Stap 1: Stel de te optimaliseren functie in.
De oppervlakte van een cirkel bereken je met de formule
![]()
Het gebied van de hele deur is dus het gebied van de rechthoek plus de helft van de omtrek:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
We hebben al de functie om te optimaliseren. Maar het hangt af van twee variabelen, terwijl het slechts van één kan afhangen.
De release vertelt ons echter dat de omtrek van de hele poort 20 meter is. De omtrek van een cirkel wordt berekend met de formule
![]()
Daarom zal de omtrek van de gehele deur zijn:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
De omtrek moet 20 m zijn. We stellen daarom de vorige uitdrukking gelijk aan 20 om de relatie tussen te vinden
![]()
En
![]()
![]()
We vermenigvuldigen alle termen met 2 om breuken te elimineren:
![]()
![]()
Wij ruimen op
![]()
![]()
![]()
En we vervangen de uitdrukking gevonden in de te optimaliseren functie:
![]()
![]()
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
![]()
![]()
Stap 3: Zoek de kritieke punten.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
Dit is een vergelijking met breuken, dus we vermenigvuldigen elke term met de lcm van de noemers om de breuken te elimineren:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Om de monotonie van de functie te bestuderen, vertegenwoordigen we het kritieke punt aan de rechterkant:
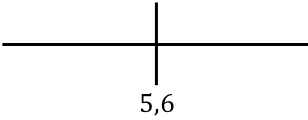
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
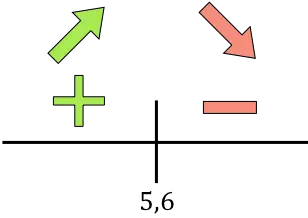
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij x=5,6, dus x=5,6 is een maximum van de functie.
Nog,
![]()
is de waarde die het maximale oppervlak oplevert. Nu berekenen we de waarde van
![]()
![]()
De waarden waaruit het maximale oppervlak bestaat, zijn dus:
![]()
![]()
Probleem 6
We willen een cilindervormige tank bouwen met een oppervlakte van 54 cm 2 . Bepaal de straal van de basis en de hoogte van de cilinder zodat het volume maximaal is.
Stap 1: Stel de te optimaliseren functie in.
Het volume van een cilinder wordt berekend met de volgende formule:
![]()
Het gebied van de basis is een cirkel, dus de formule is
![]()
. De formule voor het volume van de cilinder is daarom:
![]()
We hebben al de functie om te optimaliseren. Maar het hangt af van twee variabelen (
![]()
En
![]()
) terwijl het er maar één kan zijn. De verklaring vertelt ons echter dat de oppervlakte van de cilinder 54 cm 2 moet zijn, dus we zullen van deze voorwaarde profiteren om de relatie tussen te vinden
![]()
En
![]()
Om de oppervlakte van een cilinder te berekenen, moet je het laterale oppervlak optellen bij de oppervlakten van de twee basissen:
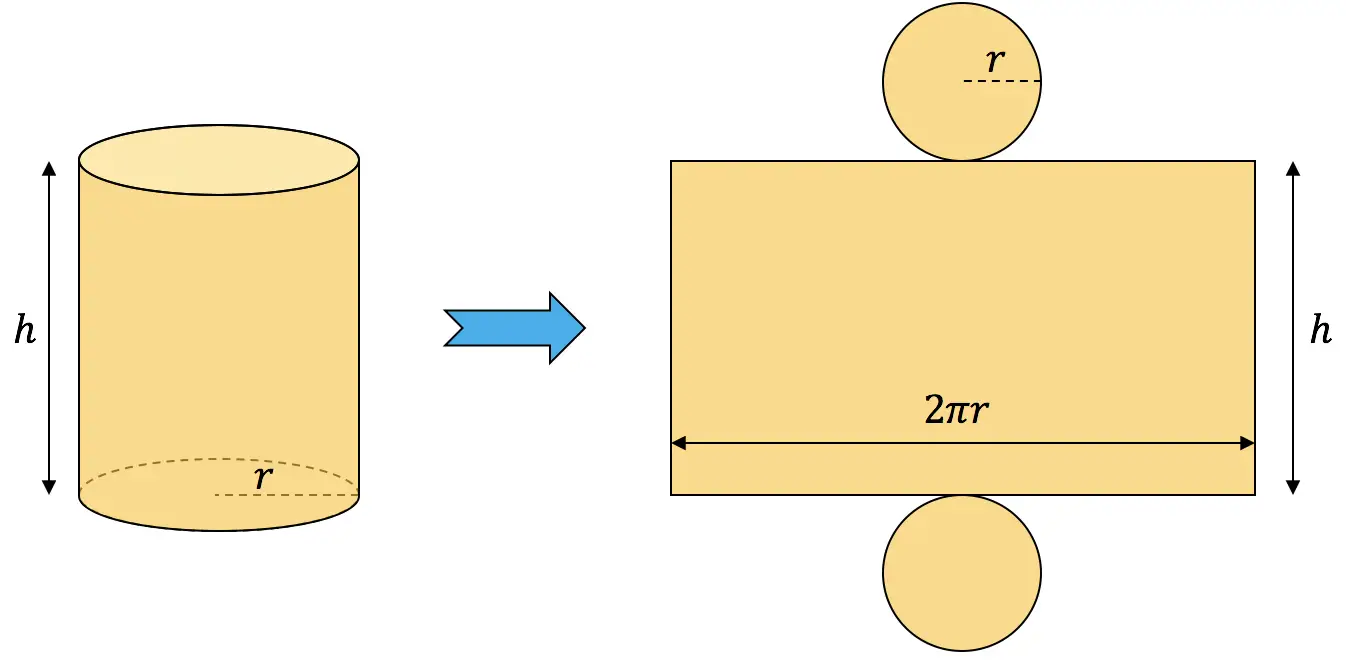
![]()
De oppervlakte van de cilinder moet 54 cm 2 zijn, dus stellen we de vorige uitdrukking gelijk aan 54 om de relatie tussen te verkrijgen
![]()
En
![]()
![]()
Wij ruimen op
![]()
![]()
![]()
En we vervangen de uitdrukking gevonden in de te optimaliseren functie:
![]()
![]()
![]()
Stap 2: Bereken de afgeleide van de te optimaliseren functie.
![]()
Stap 3: Zoek de kritieke punten.
Om de kritieke punten van de functie te vinden, lossen we op
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Stap 4: Bestudeer de monotoniciteit van de functie en bepaal het maximum of minimum van de functie.
Om de monotoniciteit van de functie te bestuderen, vertegenwoordigen we het kritieke punt op de getallenlijn:
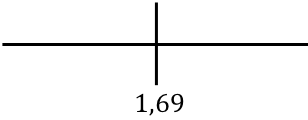
En nu evalueren we het teken van de afgeleide in elk interval, om erachter te komen of de functie stijgend of dalend is. We nemen daarom in elk interval een punt (nooit het kritieke punt) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
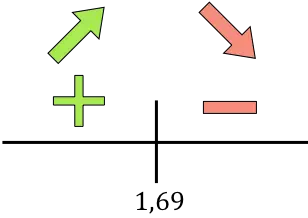
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij r=1,69, dus r=1,69 cm is een maximum van de functie.
Daarom is r=1,69 de waarde van de straal die het maximale volume oplevert. Nu berekenen we de hoogte:
![]()
Dus de waarden die het maximale volume vormen zijn:
Radio
![]()
Hoogte
![]()