Hoe u het optellen en aftrekken van een matrix kunt berekenen

Op deze pagina zullen we zien hoe je matrices kunt optellen en aftrekken . Je hebt ook voorbeelden waarmee je het perfect kunt begrijpen en opgeloste oefeningen zodat je kunt oefenen. Je vindt er ook alle eigenschappen van matrixoptelling.

Hoe matrices optellen en aftrekken?

Om een optelling (of aftrekking) van twee matrices te berekenen, moet u de elementen optellen (of aftrekken) die dezelfde positie in de matrices innemen.

Voorbeelden:

voorbeelden van optellen en aftrekken van 2x2 matrices, bewerkingen met matrices

Houd er rekening mee dat als u twee matrices wilt optellen of aftrekken, ze dezelfde dimensie moeten hebben. De volgende matrices kunnen bijvoorbeeld niet worden toegevoegd omdat de eerste een 2×2-matrix is en de tweede een 3×2-matrix:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

Opgeloste oefeningen voor het optellen en aftrekken van matrices

Oefening 1

Bereken de volgende som van 2×2 matrices:

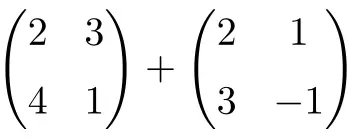
oefening stap voor stap opgelost voor toevoeging van 2x2 matrices

Het is een som van twee vierkante matrices met afmeting 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

Oefening 2

Voer de volgende matrixaftrekking uit:

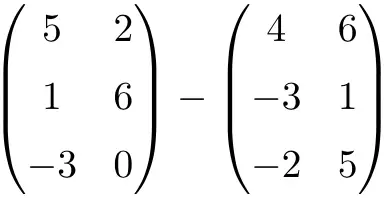
oefening opgelost stap voor stap aftrekken van matrices, bewerkingen met matrices

Het is een aftrekking van twee matrices met afmeting 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

Oefening 3

Zoek het resultaat van de volgende matrixsom van dimensie 3×3:

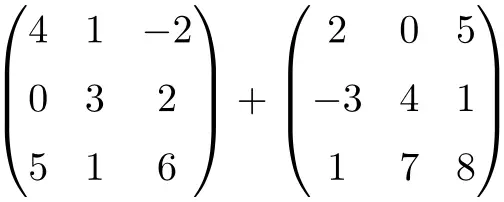
oefening stap voor stap opgelost door optelling van 3x3 matrices, bewerkingen met matrices

Het is een som van twee vierkante matrices van de orde 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

Oefening 4

Bereken de volgende optelling en aftrekking van vierkante matrices van orde 2:

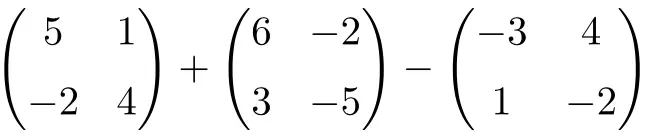
oefening opgelost stap voor stap optellen en aftrekken van 2x2 matrices, bewerkingen met matrices

Het is een bewerking gecombineerd met optellen en aftrekken van vierkante matrices van orde 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Dus voegen we eerst de matrices aan de linkerkant toe:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

En dan berekenen we het aftrekken van matrices:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

Oefening 5

Los de volgende optelling en aftrekking van de matrix op:

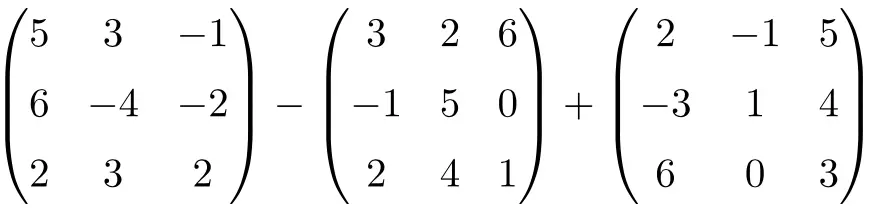
oefening opgelost stap voor stap optellen en aftrekken van 3x3 matrices, bewerkingen met matrices

Het is een gecombineerde bewerking van aftrekken en optellen van vierkante matrices van orde 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Eerst lossen we de matrixaftrekking op:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

En tenslotte voegen we de matrices toe:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

Nu je weet hoe je matrices moet optellen en aftrekken, is het een goed moment om te zien hoe je matrices kunt vermenigvuldigen , ongetwijfeld de belangrijkste matrixbewerking. Je vindt er ook opgeloste stap-voor-stap matrixvermenigvuldigingsoefeningen zodat je kunt oefenen, zoals op alle pagina’s van deze site. 😉

Voeg matrixeigenschappen toe

Matrixoptelling heeft de volgende kenmerken:

  • Matrixoptelling heeft de commutatieve eigenschap :

\displaystyle A +B = B + A

Daarom is de volgorde waarin we de matrices toevoegen hetzelfde. Om dit te demonstreren, zullen we twee matrices toevoegen door hun volgorde te veranderen en je zult zien hoe het resultaat hetzelfde is.

We gaan daarom verder met het toevoegen van twee matrices in een bepaalde volgorde:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

Merk op dat als we de volgorde van optelling van de matrices omkeren, het resultaat hetzelfde blijft:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

  • Een andere eigenschap van matrixoptelling is die van het tegenovergestelde element:

\displaystyle A + (-A) =0

Met andere woorden, als we een matrix plus dezelfde matrix toevoegen, maar waarvan alle elementen van teken veranderen, zal het resultaat een nulmatrix zijn:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

  • Matrixoptelling heeft ook de neutrale elementeigenschap:

\displaystyle A + 0 =A

Deze eigenschap is het meest voor de hand liggend. Het verwijst naar het feit dat elke matrix plus een matrix vol nullen equivalent is aan dezelfde matrix:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

  • Matrixoptelling heeft de associatieve eigenschap:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

Daarom is de volgorde waarin we de matrices toevoegen hetzelfde. Kijk naar het volgende voorbeeld, waar we 3 matrices met verschillende volgorde toevoegen en het resultaat hetzelfde is:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven