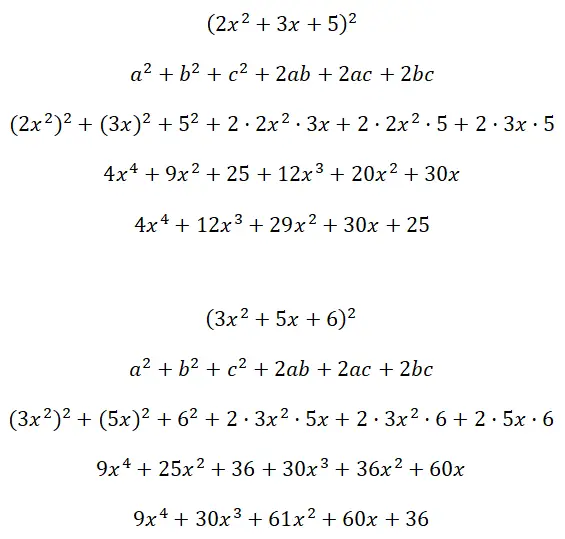Wat zijn opmerkelijke producten of opmerkelijke identiteiten?
Opmerkelijke identiteiten , ook wel opmerkelijke producten of opmerkelijke gelijkheden genoemd, zijn wiskundige hulpmiddelen waarmee producten en quotiënten van polynomen sneller kunnen worden opgelost. Zoals het woord identiteit aangeeft, zijn dit gelijkheden waarmee we deze bewerkingen kunnen berekenen zonder ze op te lossen. Omdat we weten dat deze uitdrukking vaste regels volgt (waaraan altijd wordt voldaan) en daarom kunnen we het resultaat verkrijgen zonder het te hoeven controleren.
Wanneer gebruik je een opmerkelijke identiteit?
Deze identiteiten worden voornamelijk gebruikt op het gebied van de algebra en hun belangrijkste functie is het versnellen van de oplossing van een bepaald polynoom, zonder de hele operatie zelf op te lossen. Van daaruit verkrijgen we de formules van opmerkelijke producten, waar we in het hele artikel commentaar op zullen geven. En ten slotte kunnen we de formules toepassen op volledige kwadraten, factorpolynomen of elk ander type berekening.
Hoe los je stap voor stap een opmerkelijk product op?
Om opmerkelijke identiteiten op te lossen, moet je een heel eenvoudige procedure volgen, die ook heel logisch is:
- Identificeer het type opmerkelijke identiteit: De eerste stap is het identificeren van het type operatie: een opmerkelijk product of een opmerkelijk quotiënt. Je moet ook verduidelijken welk type formule je moet toepassen, hoewel je dit later zult begrijpen, zodra we de verschillende soorten opmerkelijke identiteiten hebben uitgelegd.
- Pas de formule toe: Zodra u weet welke formule u moet toepassen, is het tijd om de berekeningen uit te voeren. Afhankelijk van het type identiteit zul je min of meer complexe operaties moeten oplossen en in de overgrote meerderheid van de gevallen zullen deze berekeningen bestaan uit termen die minstens één onbekende bevatten.
- Vereenvoudig de uitdrukking: Als u ten slotte het resultaat krijgt, moet u het vereenvoudigen. In deze stap moet u vergelijkbare termen groeperen en ordenen om een goed gestructureerde resulterende polynoom te vormen. Opgemerkt moet worden dat deze stap net zo belangrijk is als de andere, omdat de oefening anders onvolledig blijft.
Formules van opmerkelijke identiteiten of belangrijkste opmerkelijke producten
Hieronder vindt u alle formules die overeenkomen met opmerkelijke identiteiten. Naast de theoretische uitleg van elk geval zijn er ook enkele opmerkelijke opgeloste productvoorbeelden, waardoor u alle concepten beter zult begrijpen. Vermeldenswaard is dat je in dit eerste deel alleen de belangrijkste identiteiten aantreft. Maar door dit artikel te lezen, leert u hoe u complexere, opmerkelijke producten kunt ontwikkelen, zoals producten gemaakt van trinomialen.
kwadraat van een som
Het eerste geval betreft het kwadraat van de som , wat een veel voorkomende polynoomuitdrukking is in de wereld van de algebra. Dit kan geschreven worden als: (a + b) 2 , wat equivalent is aan: (a + b) · (a + b). Daarom weten we dat het kan worden opgelost met behulp van polynomiale vermenigvuldiging. Maar dankzij opmerkelijke identiteiten kunnen we tijd besparen door de volgende formule te gebruiken: (a + b) 2 = a 2 + 2ab + b 2 . Vervolgens laten we u de demonstratie zien van de formule die we zojuist hebben gezien, zodat u kunt begrijpen waar deze vandaan komt en hoe deze wordt gebruikt:
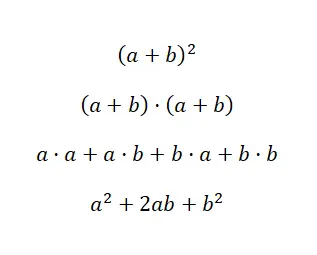
Zoals we kunnen zien, hebben we de verificatie uitgevoerd met behulp van de vermenigvuldiging van polynomen waar we eerder commentaar op hebben gegeven. En we kunnen met absolute zekerheid zeggen dat als je de resulterende formule uit je hoofd kent, je door een eenvoudige vervanging van waarden uit te voeren het resultaat sneller kunt krijgen. Het is dus een heel nuttig wiskundig concept. Nu je weet hoe het kwadraat van een som werkt, laten we je een concreet voorbeeld zien:
Voorbeeld van het kwadraat van een som
Bereken de opmerkelijke identiteit (2x + 4) 2 :
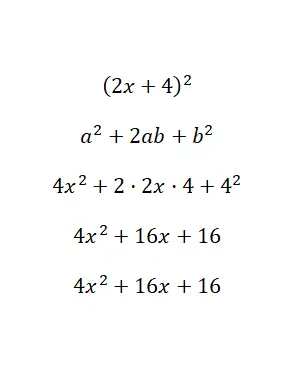
Kortom, we hebben de waarden van de binominale waarde geassocieerd met de letters van de formule en we hebben het volgende opgelost: a = 2x en b = 4. Ten slotte verkrijgen we, na het oplossen van alle berekeningen, de polynoom 4x 2 + 16x + 16, namelijk gelijk aan het origineel . In dit voorbeeld hebben we een uitgebreide polynoom (in standaardvorm) verkregen uit een gereduceerde polynoom.
kwadraat van een aftrekking
Een andere veel voorkomende uitdrukking is het kwadraat van aftrekken , dat veel lijkt op het kwadraat van optellen: het verandert slechts met één teken. Dan is de structuur van de binominale equivalent aan: (a – b) 2 , en als we deze ontvouwen krijgen we: (a – b) · (a – b). Net als in het vorige geval kan dit worden berekend uit een vermenigvuldiging van polynomen, hoewel er ook een formule is die de oplossing vergemakkelijkt: a 2 – 2ab +b 2 . Hieronder vindt u het empirische bewijs hiervan:
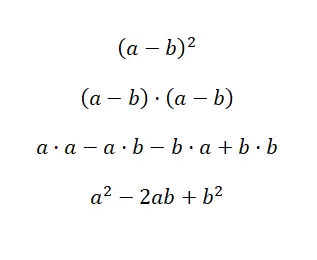
Om het oplossen van het kwadraat van een verschil te vereenvoudigen, kunnen we dezelfde formule gebruiken als voor de som van een kwadraat, maar dan met het eerste teken negatief . Door deze minimale verandering kan de uitdrukking worden aangepast aan binominale getallen die zijn samengesteld uit een positieve term en een negatieve term, wat handig is voor aftrekkingen. We laten u nu een opgelost voorbeeld zien:
Voorbeeld van het kwadraat van een aftrekking
Bereken de opmerkelijke identiteit (x – 3) 2 :
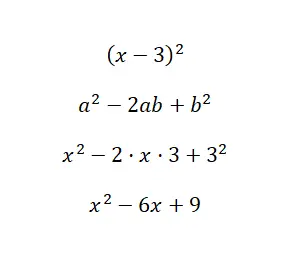
Zoals je in de voorbeeldoplossing kunt zien, hebben we de waarden van onze binominale waarde vervangen door de formule a = x en b = 3. Daarom hoeven we, met behulp van de formule die we eerder hebben uitgelegd, alleen maar de vervanging uit te voeren en enkele heel basale berekeningen. Hierdoor kunnen we zien hoe gemakkelijk het kwadraat van een verschil kan worden berekend met deze uitdrukking.
Verschil in kwadraten of som op verschil
Het derde geval van opmerkelijke producten wordt het verschil van kwadraten genoemd, dit wordt gevormd door het product van een positieve binominale en een negatieve binomiale. Een uitdrukking van deze stijl heeft de volgende structuur: (a + b) · (a – b), dus als we dit product uitbreiden, krijgen we de formule die de berekening eenvoudiger maakt: a 2 – b 2 . Zoals u kunt zien, is het een heel eenvoudige formule, hoewel u, om deze volledig te begrijpen, alle berekeningen moet ontwikkelen:
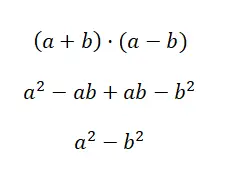
Voorbeeld van som op basis van verschil
Bereken de opmerkelijke identiteit (x + 1) · (x – 4):
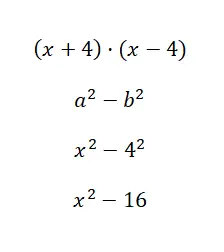
Bij deze gelegenheid is de numerieke berekening heel eenvoudig; we hoefden eigenlijk alleen maar een macht op te lossen. Hoewel het waar is dat deze formule alleen van toepassing is als de binominale termen dezelfde hoofdterm en dezelfde onafhankelijke term hebben, maar met een veranderd teken. Deze identiteit is dus belangrijk, maar het is niet degene die je het meest gaat gebruiken.
Product van twee binomialen met een gemeenschappelijke term
In dit vierde geval worden we geconfronteerd met een situatie die sterk lijkt op de vorige, zij het met een kleine wijziging in de structuur. Observeer het verschil dat we je laten zien: (x + a) · (x + b) en (a + b) · (a – b). Mocht je het nog steeds niet zo duidelijk zien, overweeg dan het volgende voorbeeld: (x + 4) · (x + 5) en (x + 4) · (x – 4). In het eerste geval (het product van twee gemeenschappelijke binominale termen ) is er slechts één gedeelde term, terwijl in het tweede geval (de som op basis van verschil) de twee termen gemeenschappelijk zijn, maar de onafhankelijke term een omgekeerd teken heeft. Dat gezegd hebbende, laten we eens kijken met welke formule we kunnen handelen:
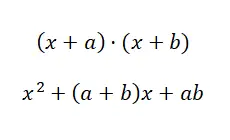
Voorbeeld van het product van twee binomialen met een gemeenschappelijke term
Los het opmerkelijke product op (x + 2) · (x + 3):
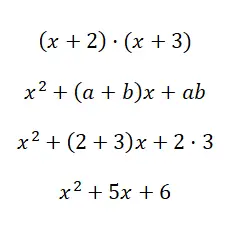
Met behulp van de formule x 2 + (a + b)x + ab kunnen we de tweedegraadspolynoom berekenen die voortkomt uit de vermenigvuldiging van de twee binominale getallen. We hopen dat je door dit voorbeeld het verschil hebt begrepen tussen de laatste twee gevallen die we hebben uitgelegd, omdat het soms moeilijk kan zijn om ze van elkaar te onderscheiden.
kwadraat van een trinominaal
Wanneer we het kwadraat van een trinominaal proberen te berekenen, hebben we ook een opmerkelijk product dat ons leven gemakkelijker maakt. Deze uitdrukking wordt als volgt weergegeven: (a + b + c) 2 en het equivalente product is: a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. Opgemerkt moet worden dat dit geldig is in het geval van een positieve trinominaal, maar als een van de coëfficiënten negatief is, hoeft u alleen maar de negatieve waarde in de formule te schrijven. Hieronder vindt u de demonstratie van de formule:
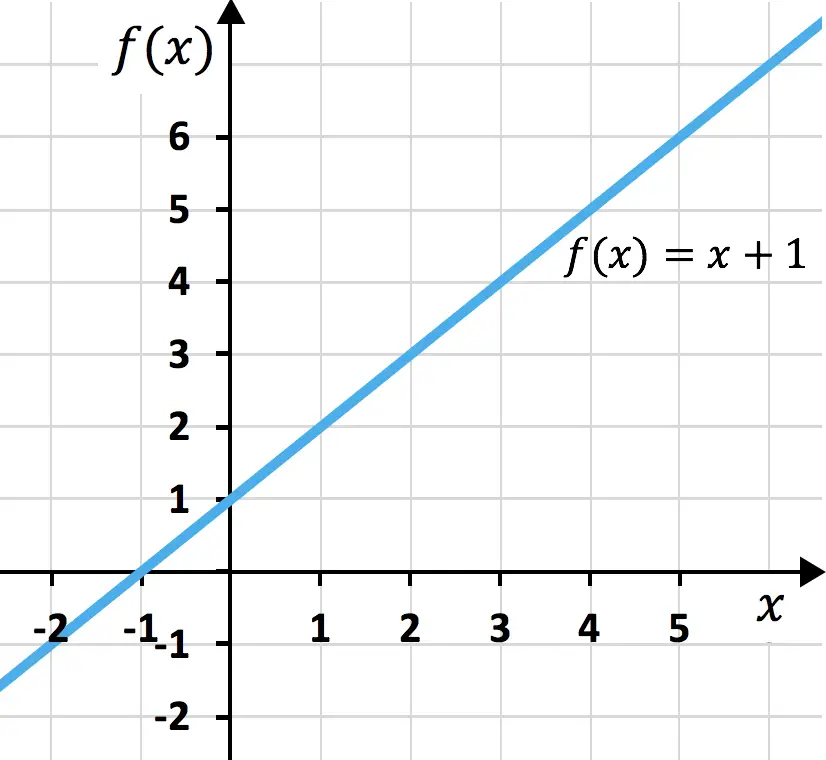
Voorbeeld van het kwadraat van een trinominaal
Bereken de opmerkelijke identiteit (2x + 1 + x 2 ) 2 :
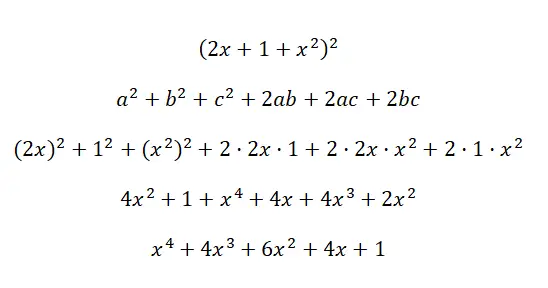
Opmerkelijke identiteitsformules of opmerkelijke kubusproducten
Nu we de belangrijkste opmerkelijke identiteiten hebben uitgelegd, zullen we kijken naar hun afgeleiden , te beginnen met de kubusvormige binomialen. Om opmerkelijke producten van deze stijl te berekenen, zullen we onze toevlucht moeten nemen tot formules die iets complexer zijn, maar die een vergelijkbare structuur volgen als de formules die we al hebben besproken.
binomiaal in blokjes
De kubus van een binomiaal wordt geschreven: (a + b) 3 en (a – b) 3 , deze uitdrukking is equivalent aan de volgende formule: (a 3 + 3a 2 b + 3ab 2 + b 3 ), en (a 3 – 3a 2 b + 3ab 2 – b 3 ). Deze twee gevallen worden de kubus van een som en de kubus van een aftrekking genoemd, omdat het gekubeerde binomialen zijn. Hieronder vindt u een zeer gedetailleerde demonstratie van elk geval:
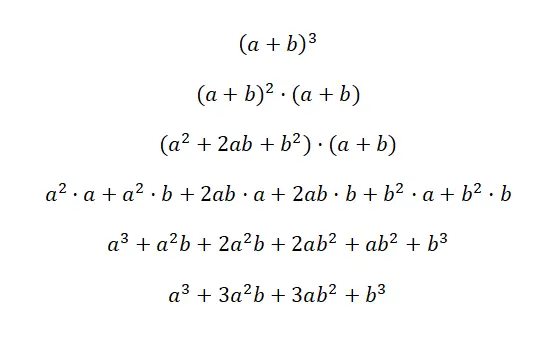
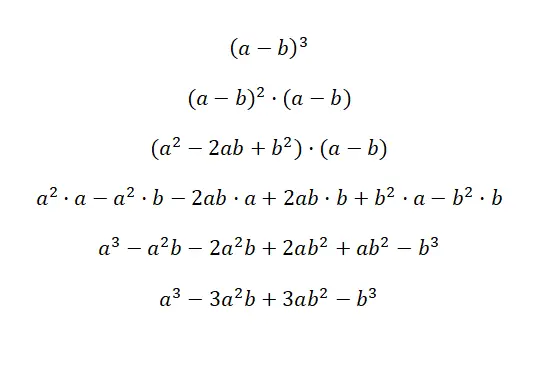
De sleutel tot het begrijpen van dit eerste bewijs is begrijpen dat (a + b) 3 equivalent is aan: (a + b) 2 · (a + b). Op deze manier gebruiken we de formule voor het kwadraat van een som , die we eerder hebben uitgelegd, om de andere factor te vermenigvuldigen. Vervolgens vereenvoudigen we eenvoudigweg de uitdrukking en verkrijgen we de overeenkomstige opmerkelijke identiteit: a 3 + 3a 2 b + 3ab 2 + b 3 . In het geval van het tweede voorbeeld gebeurt hetzelfde, maar met een verandering van teken.
Voorbeeld van een binomiale kubus
Los opmerkelijke identiteit op (x + 3) 3 :
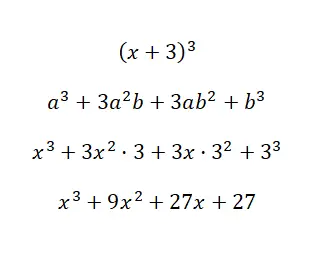
Met behulp van de formule die we zojuist hebben besproken, kunnen we de polynoom berekenen, rekening houdend met het volgende: a = xyb = 3. Zoals u kunt zien, is de procedure heel eenvoudig en levert deze niet veel complicaties op bij de berekening. Dat komt omdat we de formule hebben . Anders zou het behoorlijk vervelend zijn om zoveel te moeten vermenigvuldigen.
Som van kubussen en verschil van kubussen
We hebben ook dit andere geval, dat gemakkelijk kan worden verward met het vorige. Hoewel de twee gevallen verschillend zijn geschreven, zijn ze niet gelijkwaardig. De uitdrukking die overeenkomt met de som of het verschil van de kubussen is: a 3 + b 3 , terwijl we in het vorige geval spraken van: (a + b) 3 . Zoals je kunt zien, is er een onmiskenbare gelijkenis in de structuur van de uitdrukking, maar in werkelijkheid zijn het, als het gaat om het ontwikkelen van de berekening, twee totaal verschillende gevallen:
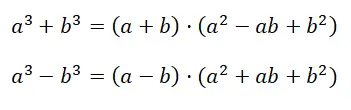
Bij de demonstratie van de formule verkrijgen we de factorisatie van de eerste polynoom , precies gaan we van de initiële binominale naar het product van een binominale door een trinomiale. Het lijkt erop dat het verkregen resultaat (a + b) · (a 2 – ab + b 2 ), de berekening helemaal niet vereenvoudigt, maar in werkelijkheid krijgen we door de polynoom in factoren te ontbinden een uitdrukking die heel gemakkelijk te begrijpen is.
Voorbeeld van de som van kubussen
Bereken het opmerkelijke product x 3 + 27:
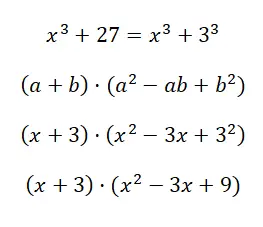
In dit geval is het resultaat dat we krijgen behoorlijk lang, omdat het niet verder kan worden vereenvoudigd. Maar het is normaal om tot deze uitdrukking te komen, in feite kun je in deze gevallen alleen een resultaat verkrijgen met de structuur die gelijkwaardig is aan het product van een binomiaal door een trinominaal, zoals in dit voorbeeld.
trinominaal in blokjes
De kubus van een trinomiaal wordt geschreven: (a + b + c) 3 , wat neerkomt op het vermenigvuldigen van drie identieke trinomialen, maar zonder exponent: (a + b + c) · (a + b + c) · (a + b + c). Het is het meest complexe opmerkelijke product dat er is, hoewel de formule vrij logisch is en op dezelfde manier wordt verkregen als alle andere, wanneer je de overeenkomstige vermenigvuldigingen van polynomen uitvoert. Hieronder vindt u het bewijs van de formule voor deze opmerkelijke identiteit:
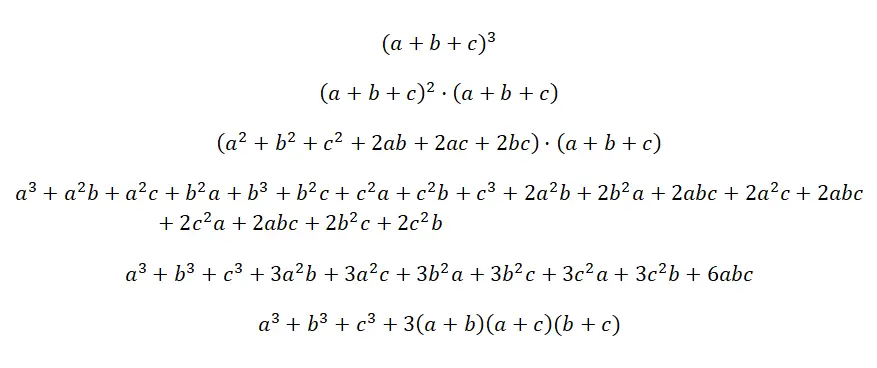
Voorbeeld van de kubus van een trinominaal
Los de volgende trinomiale kubus op (x 2 + 3x – 4) 3 :
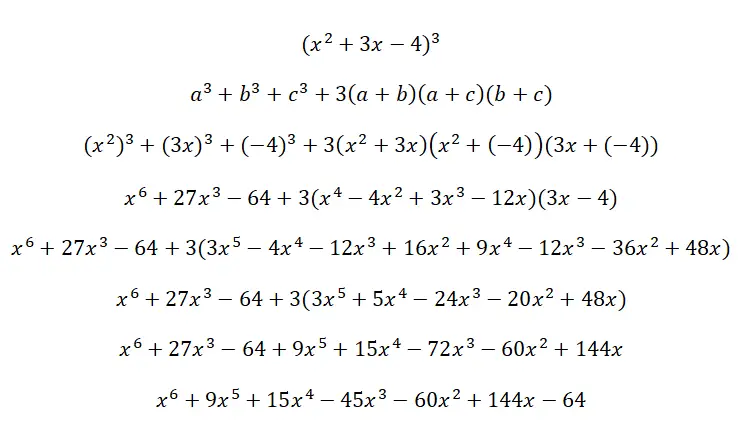
opmerkelijke verhoudingen
Ten slotte zullen we opmerkelijke quotiënten uitleggen, wat opmerkelijke identiteiten zijn voor het snel oplossen van bepaalde soorten algebraïsche breuken. Om precies te zijn, er zijn vier verschillende typen, die één kenmerk gemeen hebben: hun resultaat bestaat uit exacte polynomen (waarbij de rest gelijk is aan nul). Het is ook de moeite waard te vermelden dat de formules van opmerkelijke quotiënten een bepaalde relatie hebben met de formules van opmerkelijke producten die we al hebben uitgelegd.
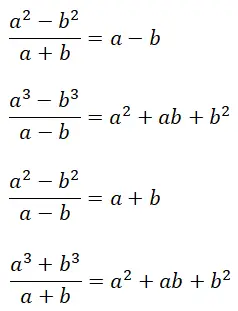
Voorbeeld van opmerkelijke verhoudingen opgelost
Bereken de volgende opmerkelijke verhoudingen:
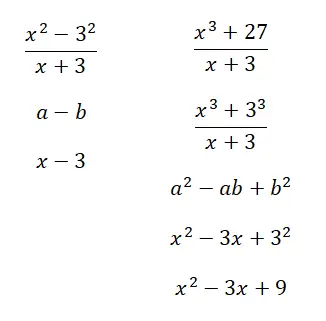
Opmerkelijke productoefeningen opgelost
Nu je weet hoe de verschillende notabelen worden opgelost, is het tijd om een beetje te oefenen. Daarom bieden wij je 6 oefeningen aan om alle uitgelegde theorie toe te passen. En we laten je een tabel zien met de belangrijkste opvallende identiteiten, zodat je deze bij de hand hebt terwijl je alle oefeningen oplost:

Oefening 1
Los de binomiale vierkanten (x – 4) 2 , (x + 1) 2 en (x – 3) 2 op:
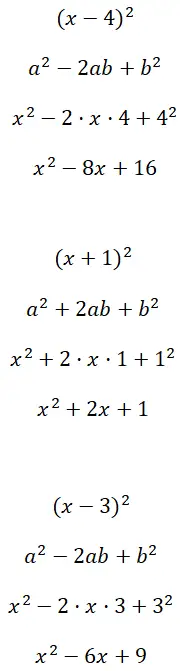
Oefening 2
Bereken de twee verschillen tussen vierkanten (x – 1) · (x + 1) en (x + 3) · (x – 3):
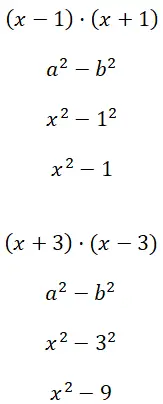
Oefening 3
Ontwikkel de opmerkelijke producten tot de kubus (x – 5) 3 en (x + 8) 3 :
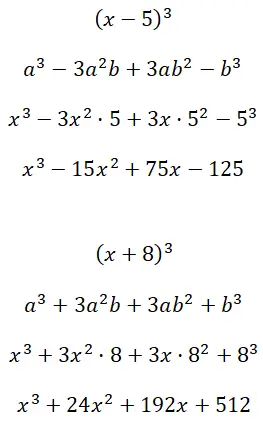
Oefening 4
Ontwikkel opmerkelijke identiteiten gevormd uit multi-factor termen (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) en (5xy 2 – 2xy) 2 :
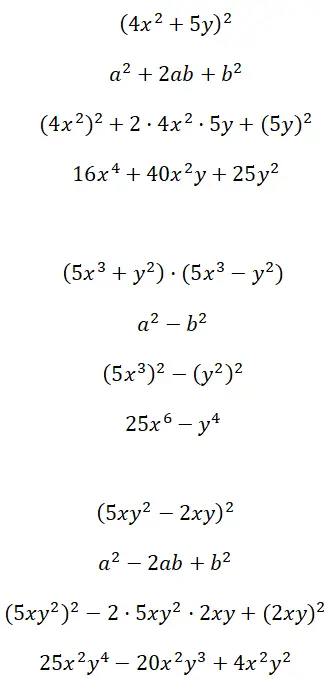
Oefening 5
Bereken de opmerkelijke kubieke producten gevormd door de multifactortermen (3x 2 + y) 3 en (5y 3 – 2x 2 ) 3 :
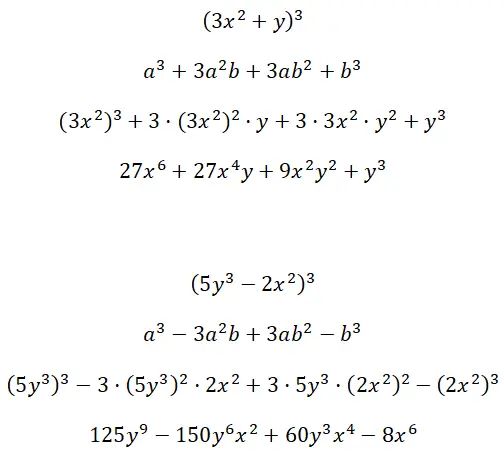
Oefening 6
Los de kwadraten op van de trinomialen (2x 2 + 3x + 5) 2 en (3x 2 + 5x + 6):