Oneindige onbepaaldheid tussen oneindigheid (∞/∞)

In dit artikel leggen we uit hoe je de oneindigheid van onbepaaldheid tussen oneindigheid (∞/∞) kunt berekenen. Voorbeelden van deze onbepaaldheid vind je met allerlei functies: polynomiale, radicale, exponentiële functies, enz. Bovendien kun je trainen met oefeningen die stap voor stap worden opgelost met limieten die oneindige onbepaaldheid tussen oneindigheden opleveren.

Hoe oneindige onbepaaldheid tussen oneindig op te lossen

Wanneer de limiet van een functie oneindig gedeeld door oneindig geeft, betekent dit dat het een onbepaaldheid (of onbepaalde vorm) is. Om de limiet op te lossen van een functie die oneindigheid of onbepaaldheid tussen oneindigheid geeft, moet de graad van het tellerpolynoom worden vergeleken met de graad van het noemerpolynoom.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

Het resultaat van onbepaaldheid oneindig gedeeld door oneindig hangt af van de graad van de teller en de graad van de noemer van de breuk:

Als de graad van het tellerpolynoom kleiner is dan de graad van het noemerpolynoom, is de oneindigheid van onbepaaldheid gedeeld door oneindig gelijk aan nul.
Als de graad van het tellerpolynoom gelijk is aan de graad van het noemerpolynoom, is de oneindige onbepaaldheid over oneindig het quotiënt van de leidende coëfficiënten van de twee polynomen.
Als de graad van het tellerpolynoom groter is dan de graad van het noemerpolynoom, geeft de oneindigheid van onbepaaldheid tussen oneindigheid min of meer oneindigheid (het teken hangt af van de hoofdtermen van de twee polynomen).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ Voorbeelden van oneindige onbepaaldheid tussen oneindigheid

Laten we eens kijken hoe de onbepaalde vorm oneindig tussen oneindigheid wordt opgelost door naar verschillende voorbeelden van elk geval te kijken:

De graad van de teller is kleiner dan de graad van de noemer

Zoals we hierboven hebben gezien, geeft de oneindige onbepaalde grens tussen oneindigheid altijd 0 als de graad van het tellerpolynoom kleiner is dan de graad van het noemerpolynoom.

Voorbeeld 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

De polynoom van de teller is van de tweede graad, terwijl die van de noemer van de derde graad is, dus de oplossing van de limiet is 0.

Voorbeeld 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

De polynomiale functie van de teller is van de eerste graad, maar de functie van de noemer is van de vierde graad, dus de limiet voor negatieve oneindigheid is 0.

De graad van de teller is gelijk aan de graad van de noemer

Wanneer de graad van het tellerpolynoom gelijk is aan de graad van het noemerpolynoom, wordt de onbepaalde limiet oneindig door oneindig berekend door de leidende coëfficiënten (coëfficiënt van de hogere graadterm) van de twee polynomen te delen.

Voorbeeld 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

In dit geval zijn de twee polynomen van de tweede graad. Daarom is het noodzakelijk om de coëfficiënten van de termen van hogere graad te delen om de limiet op positief oneindig te vinden.

Voorbeeld 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

Hoewel de limiet ligt wanneer x de neiging heeft minus oneindig te zijn, wordt de oneindige onbepaaldheid tussen oneindigheid op dezelfde manier opgelost.

De graad van de teller is groter dan de graad van de noemer

Wanneer de graad van het tellerpolynoom groter is dan de graad van het noemerpolynoom, zal de onbepaalde vorm van oneindigheid tussen oneindigheid altijd oneindigheid opleveren, en wordt het teken van oneindigheid bepaald door de termen van de hogere graad van de twee polynomen.

Voorbeeld 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

De functie van de teller heeft een hogere graad dan die van de noemer, dus de onbepaaldheid oneindigheid op oneindig geeft oneindigheid. Bovendien krijgen in dit geval zowel de teller als de noemer een positieve oneindigheid, dus het resultaat van de limiet moet ook positief zijn.

Voorbeeld 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

In dit probleem wordt een positieve oneindigheid verkregen uit de teller omdat elke kwadratische term positief is, terwijl daarentegen een negatieve oneindigheid wordt verkregen uit de noemer. Daarom is de resulterende limiet negatief omdat positief gedeeld door negatief gelijk is aan negatief.

Oneindige onbepaaldheid tussen oneindigheid met wortels

We hebben zojuist gezien hoe we de oneindige onbepaaldheid tussen oneindigheid kunnen berekenen als we polynomiale functies hebben. Maar… hoeveel is oneindig gedeeld door oneindig als we wortels hebben?

De graad van een irrationele functie (functie met wortels) is het quotiënt tussen de graad van de hoofdterm en de index van de radicaal.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Als de limiet van een functie met wortels de onbepaaldheid tussen oneindig geeft , moeten we daarom dezelfde regels toepassen als hierboven uitgelegd voor de graden van de teller en de noemer, maar er rekening mee houden dat de graad van een polynoom met wortels anders wordt berekend.

Kijk naar het volgende voorbeeld van de limiet tot oneindig van een functie met radicalen:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

De graad van de teller is 2 en de graad van de noemer is 4 (8/2=4). Daarom is de limiet 0 omdat de graad van de teller kleiner is dan de graad van de noemer.

Aan de andere kant, als de graad van de teller en de noemer gelijk zijn, moeten we, om de onbepaalde limiet te berekenen, de hoofdcoëfficiënt met de radicaal nemen:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

Oneindige onbepaaldheid tussen oneindigheid met exponentiële functies

Ten slotte hoeven we alleen maar een geval van het onbepaaldheidsquotiënt van oneindigheden te bestuderen: hoeveel bedraagt de oneindige onbepaaldheid tussen oneindigheid en exponentiële functies.

De groei van een exponentiële functie is veel groter dan de groei van een polynomiale functie, dus we moeten bedenken dat de graad van een exponentiële functie groter is dan de graad van een polynomiale functie.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Daarom, als oneindige onbepaaldheid gedeeld door oneindig het resultaat is van een limiet met exponentiële functies, is het voldoende om dezelfde regels toe te passen die zijn uitgelegd voor de graden van de teller en de noemer, maar rekening houdend met het feit dat een exponentiële functie van een hogere orde is dan een polynoom. . Bovendien, als we exponentiële functies hebben in de teller en de noemer van de deling, zal de exponentiële functie met de grotere basis van hogere orde zijn. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

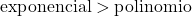
In dit geval wordt de noemer gevormd door een exponentiële functie en is deze dus van hogere orde dan de teller. Daarom verdwijnt de onbepaalde vorm oneindig tussen oneindigheid.

Opgeloste oefeningen van oneindige onbepaaldheid tussen oneindigheid

Oefening 1

Bereken de limiet van de volgende rationale functie:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

zie oplossing

Bij het berekenen van de limiet krijgen we de oneindige onbepaaldheid tussen oneindigheid, maar aangezien de graad van de teller kleiner is dan de graad van de noemer, is de onbepaalde limiet gelijk aan nul.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

Oefening 2

Los de volgende onbepaalde limiet op:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

zie oplossing

Wanneer u de limiet probeert te berekenen, wordt de onbepaaldheid ∞/∞ verkregen. In dit geval is de graad van het tellerpolynoom groter dan de graad van het noemerpolynoom, dus de onbepaalde limiet is gelijk aan plus oneindig.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

Oefening 3

Los de volgende limiet op oneindig op:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

zie oplossing

De limiet geeft onbepaaldheid minus oneindig tussen plus oneindig. De graad van de teller is groter dan de graad van de noemer, dus de onbepaalde limiet is gelijk aan plus oneindig. Omdat de deling echter negatief oneindig door positief oneindig is, is het resultaat minus oneindig.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Oefening 4

Los de volgende onbepaalde limiet op:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

zie oplossing

In dit probleem wordt de oneindige onbepaalde vorm over oneindig verkregen uit het quotiënt van twee polynomen van dezelfde graad, daarom is het resultaat van de onbepaalde limiet de verdeling van hun hoofdcoëfficiënten:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Oefening 5

Bereken de volgende limiet minstens tot in het oneindige:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

zie oplossing

De graad van de algebraïsche uitdrukking van de teller is kleiner dan de graad van de uitdrukking van de noemer, dus de onbepaaldheid +∞/+∞ geeft 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Oefening 6

Los de volgende onbepaalde limiet van een functie met wortels op:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

zie oplossing

De uitdrukking voor de teller staat onder een radicaal, dus de graad ervan is 7/3. Aan de andere kant is de polynoom in de noemer kwadratisch. En aangezien 7/3>2 geeft de limiet plus oneindig:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

Oefening 7

Bepaal de limiet tot oneindig van de volgende functie met breuken:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

zie oplossing

In deze oefening wordt de onbepaaldheid minus oneindig gedeeld door min oneindig verkregen waarbij de graad van de teller groter is dan de graad van de noemer, dus:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Oefening 8

Zoek de limiet tot ten minste oneindig van de volgende functie:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

zie oplossing

Het noemerpolynoom is kwadratisch, terwijl het tellerpolynoom lineair is. Daarom geeft oneindigheid van onbepaaldheid gedeeld door oneindigheid 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Oefening 9

Los de ten minste oneindige limiet op van de volgende functie:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

zie oplossing

De teller is van grotere graad dan de noemer, dus het resultaat van de onbepaalde vorm ∞/∞ zal oneindig zijn. Bovendien zal het oneindigheidsteken negatief zijn omdat het positieve gedeeld door het negatieve het negatieve oplevert:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Oefening 10

Los de volgende limiet op met oneindige onbepaaldheid tussen oneindig:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

zie oplossing

De exponentiële functie is van een hogere orde dan de polynomiale functie, dus de limiet geeft oneindigheid. Als u het positieve door het negatieve deelt, is het oneindigheidsteken echter negatief:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Oefening 11

Bereken de volgende limiet:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

zie oplossing

In dit probleem wordt de onbepaaldheid oneindig op oneindig opgelost door de dominante coëfficiënten van de twee polynomen te delen, aangezien ze van dezelfde graad zijn:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

Oefening 12

Los de limiet van de volgende functie op als x oneindig nadert:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

zie oplossing

Hoewel het onbekende in de teller niet direct in het kwadraat wordt gebracht, kunnen we bij het oplossen van de opmerkelijke identiteit duidelijk zien dat de graad van de teller groter is dan de graad van de noemer. Nog:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Oefening 13

Bereken de limiet tot oneindig van de volgende functie met een derdemachtswortel:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

zie oplossing

De teller bestaat uit een derdemachtswortel, dus de graad ervan is 3/3=1. Dan is de graad van de teller gelijk aan die van de noemer, dus de oneindige onbepaaldheid tussen oneindigheid wordt als volgt opgelost:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

Oefening 14

Los de limiet tot oneindig op van de volgende functie met twee radicalen:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

zie oplossing

De graad van de teller is 7/3 = 2,33 en de graad van de noemer is 5/2 = 2,5. Daarom, aangezien de graad van de teller kleiner is dan de graad van de noemer, is de onbepaalde oneindige limiet tussen oneindigheid 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Oefening 15

Bereken de volgende limiet:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

zie oplossing

Ongeacht de graad van de teller, aangezien we een exponentiële functie in de noemer hebben, is het resultaat van de onbepaalde vorm oneindig boven oneindig 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Oneindige onbepaaldheid tussen oneindig (∞/∞)

Hoe oneindige onbepaaldheid tussen oneindig op te lossen

De graad van de teller is kleiner dan de graad van de noemer

Voorbeeld 1:

Voorbeeld 2:

De graad van de teller is gelijk aan de graad van de noemer

Voorbeeld 3:

Voorbeeld 4:

De graad van de teller is groter dan de graad van de noemer

Voorbeeld 5:

Voorbeeld 6:

Oneindige onbepaaldheid tussen oneindigheid met wortels

Oneindige onbepaaldheid tussen oneindigheid met exponentiële functies

Opgeloste oefeningen van oneindige onbepaaldheid tussen oneindigheid

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Oefening 8

Oefening 9

Oefening 10

Oefening 11

Oefening 12

Oefening 13

Oefening 14

Oefening 15

Laat een reactie achter Reactie annuleren