Op deze pagina leggen we uit wat de onafhankelijke term van een polynoom is en hoe deze wordt berekend. Daarnaast kun je verschillende voorbeelden zien van hoe je de onafhankelijke term van verschillende polynomen kunt identificeren en zelfs oefenen met opgeloste oefeningen.
Wat is de onafhankelijke term van een polynoom?
De definitie van de onafhankelijke term van een polynoom is als volgt:
In de wiskunde is de onafhankelijke term van een polynoom de term die geen variabele heeft. Daarom komt de onafhankelijke term van een polynoom overeen met de monomial van nul graden van de polynoom.
De onafhankelijke term van de volgende polynoom is bijvoorbeeld 7:
![]()
In de polynoom van het vorige voorbeeld is de term die geen letterlijk deel heeft, dat wil zeggen geen x heeft, het getal 7. Om deze reden is de onafhankelijke term van genoemde polynoom 7.
Hoewel de onafhankelijke term van een polynoom een heel eenvoudig concept lijkt, weet u dat deze zeer nuttig is voor sommige polynoomberekeningen. De procedure voor het vinden van de wortels van een polynoom begint bijvoorbeeld bij de onafhankelijke term ervan. Als je meer wilt weten over hoe je de wortels (of nullen) van een polynoom kunt vinden, kun je deze link bekijken, waar je ook voorbeelden kunt zien en kunt oefenen met oefeningen die stap voor stap worden opgelost.
Voorbeelden van onafhankelijke termen van polynomen
Zodra we de betekenis van de onafhankelijke term van een polynoom kennen, zullen we verschillende voorbeelden zien van hoe we de onafhankelijke term van een polynoom kunnen vinden:
- Voorbeeld van een onafhankelijke term van een polynoom van graad 4:
![]()
De polynoom in dit voorbeeld is een monische polynoom en de term die geen variabele heeft is 5, dus de waarde van de onafhankelijke term van de polynoom is 5.
- Voorbeeld van een onafhankelijke term van een polynoom van graad 5:
![]()
Het element van deze polynoom dat niet vergezeld gaat van de variabele x is -2, het is daarom de onafhankelijke term van de polynoom. Merk op dat het negatieve teken van het getal ook is opgenomen in de onafhankelijke term.
- Voorbeeld van een onafhankelijke term van een polynoom van graad 8:
![]()
Alle monomialen in deze polynoom hebben een variabele behalve +1, dus de onafhankelijke term van de polynoom is +1.
Tenslotte is een van de eigenschappen van de onafhankelijke term dat de numerieke waarde van een polynoom voor x=0 altijd gelijk is aan zijn onafhankelijke term. Als je meer geïnteresseerd bent in dit merkwaardige ding, kun je op de gelinkte pagina raadplegen hoe de numerieke waarde van een polynoom wordt berekend, daarnaast vind je ook verschillende voorbeelden van hoe dit wordt gedaan en kun je oefenen met opgeloste oefeningen stap voor stap.
Opgeloste oefening over de onafhankelijke term van een polynoom
Om te voltooien wat de onafhankelijke term van een polynoom is, raden we u aan de oefening te doen die we hieronder oplossen:
- Gegeven de polynoom
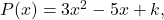
berekent de waarde van de onafhankelijke term

zodat deze gevuld is
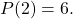
Het eerste dat u moet doen om dit probleem op te lossen, is proberen vast te stellen
![]()
Nog:
![]()
We berekenen het vermogen:
![]()
We doen de vermenigvuldigingen:
![]()
En we trekken af als termen:
![]()
Om aan de voorwaarde van de verklaring te voldoen, is het dus noodzakelijk om de verkregen algebraïsche uitdrukking gelijk te stellen aan 6:
![]()
![]()
Het is daarom voldoende om de resulterende vergelijking op te lossen:
![]()
![]()
Concluderend moet de onafhankelijke term van de polynoom 4 zijn.
Ten slotte moet u weten dat de onafhankelijke term van een polynoom ook belangrijk is om de regel van Ruffini correct toe te passen. Voor het geval je niet weet wat het is: de regel van Ruffini is een methode die wordt gebruikt om polynomen snel te delen. Hier kunt u zien hoe u de regel van Ruffini moet uitvoeren en hoe deze zich verhoudt tot de onafhankelijke term van een polynoom.