Bereik van een array op basis van een parameter -

Op deze pagina ziet u hoe u de rangorde van een tabel kunt berekenen op basis van een parameter. Ook vindt u stapsgewijze voorbeelden en opgeloste oefeningen over hoe u het bereik van een matrix kunt vinden op basis van één parameter.

Om de procedure voor het bestuderen van de rangorde van matrices met parameters volledig te begrijpen, is het belangrijk dat u al weet hoe u de rangorde van een matrix op basis van determinanten kunt berekenen . We raden u daarom aan eerst deze twee dingen te leren voordat u verder leest.

Hoe u het bereik van een array kunt berekenen op basis van een parameter. Voorbeeld:

Bepaalt het bereik van matrix A op basis van verschillende parameterwaarden
$\displaystyle a :$

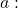
$\displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}$

Matrix A heeft hoogstens rang 3, omdat het een matrix van orde 3 is. Daarom moeten we eerst de determinant van de gehele 3×3-matrix oplossen met de regel van Sarrus , om te zien of deze rang 3 kan zijn:

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}$

Het resultaat van de determinant is een functie van de parameter

$\displaystyle a$

. We stellen daarom het resultaat gelijk aan 0 om te zien wanneer de tafel van rang 2 zal zijn en wanneer deze van rang 3 zal zijn:

$\displaystyle -a^2+1 = 0$

En we lossen de resulterende vergelijking op:

$\displaystyle a^2 = 1$

$\displaystyle \sqrt{a^2} = \sqrt{1}$

$\displaystyle \bm{a = \pm 1}$

Daarom, wanneer

$\displaystyle a$

Of het nu +1 of -1 is, de 3×3 determinant zal 0 zijn en daarom zal de rangorde van de matrix niet 3 zijn. Aan de andere kant, wanneer

$\displaystyle a$

verschillend is van +1 en -1, zal de determinant verschillend zijn van 0 en daarom zal de matrix van rang 3 zijn.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle \bm{a=+1} :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}$

Zoals we eerder zagen, wanneer

$\displaystyle a$

is 1, de determinant van de matrix is 0. Deze kan daarom niet van rang 3 zijn. We proberen nu een 2×2 determinant te berekenen die verschilt van 0 binnen de matrix, bijvoorbeeld die van de linkerbovenhoek:

$\displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0$

De determinant van orde 2 is anders dan 0. Dus als de parameter

$\displaystyle a$

of +1, de rangorde van de matrix is 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Zodra we het bereik van de matrix zien wanneer

$\displaystyle a \neq +1,-1$

en wanneer

$\displaystyle a=+1$

Laten we eens kijken wat er wanneer gebeurt

$\displaystyle \bm{a = -1} :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}$

Zoals we in het begin zagen, wanneer

$\displaystyle a$

es -1 en de determinant van de matrix is 0. Daarom kan deze niet op rang 3 worden gezet. Daarom moeten we proberen een determinant van 2×2 in de matrix tegen te komen die anders is dan 0, bijvoorbeeld de lagere onderdeel van de matrix. LINKS:

$\displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0$

De determinant van dimensie 2 is anders dan 0. Dus als de parameter

$\displaystyle a$

of -1, de rangorde van de tafel is 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

We hebben daarom 3 verschillende gevallen gevonden waarin de rangorde van matrix A afhangt van de waarde die de parameter aanneemt

$\displaystyle a.$

Hier is de samenvatting :

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Nu u weet hoe u de reeks parameterafhankelijke matrices moet bespreken, kunt u oefenen met de onderstaande stapsgewijze oefeningen. Om ze op te lossen, zullen de eigenschappen van de determinatoren je zeker helpen, dus als je er niet erg duidelijk over bent, raad ik je aan eerst een kijkje te nemen op de gelinkte pagina, waar ze allemaal met voorbeelden worden uitgelegd.

Problemen met op parameters gebaseerde matrixbereiken opgelost

Oefening 1

Bestudeer het bereik van de volgende tabel op basis van de parameterwaarde

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

zie oplossing

Matrix A heeft maximaal rang 3, omdat het een 3×3-matrix is. Daarom moeten we eerst de determinant van de hele matrix oplossen (met de regel van Sarrus), om te zien of deze van rang 3 kan zijn:

$\displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4$

We stellen het resultaat gelijk aan 0 om te zien wanneer de array rang 2 zal zijn en wanneer rang 3:

$\displaystyle -2a+4=0$

$\displaystyle -2a=-4$

$\displaystyle a=\cfrac{-4}{-2} = 2$

Daarom, wanneer

$\displaystyle a$

verschillend is van 2, zal de determinant 3×3 anders zijn dan 0 en daarom zal de rangorde van de matrix 3 zijn.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 2 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=2 :$

$\displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

We hebben daarom 2 gevallen gevonden waarin het bereik van matrix A varieert met de waarde die de parameter aanneemt:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Oefening 2

Zoek het bereik van de volgende tabel op basis van de parameterwaarde

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}$

zie oplossing

Matrix A heeft maximaal rang 3, omdat het een 3×3-matrix is. Daarom moeten we eerst de determinant van de hele matrix oplossen (met de regel van Sarrus), om te zien of deze van rang 3 kan zijn:

$\displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}$

We stellen het resultaat gelijk aan 0 om te zien wanneer de array rang 2 zal zijn en wanneer rang 3:

$\displaystyle 2-2a^2=0$

$\displaystyle -2a^2=-2$

$\displaystyle a^2=\cfrac{-2}{-2}$

$\displaystyle a^2=1$

$\displaystyle a=\pm 1$

Daarom, wanneer

$\displaystyle a$

verschillend is van +1 en -1, zal de 3×3-determinant anders zijn dan 0 en daarom zal de rangorde van de matrix 3 zijn.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1, -1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=+1 :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=-1 :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

We hebben daarom 3 gevallen gevonden waarin het bereik van matrix A varieert afhankelijk van de waarde die de parameter aanneemt:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Oefening 3

Berekent het bereik van de volgende tabel op basis van de parameterwaarde

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}$

zie oplossing

Matrix A heeft maximaal rang 3, omdat het een 3×3-matrix is. Daarom moeten we eerst de determinant van de hele matrix oplossen (met de regel van Sarrus), om te zien of deze van rang 3 kan zijn:

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}$

We stellen het resultaat gelijk aan 0 om te zien wanneer de array rang 2 zal zijn en wanneer rang 3:

$\displaystyle a^2+4a=0$

Dit is een onvolledige kwadratische vergelijking, dus we halen er een gemeenschappelijke factor uit:

$\displaystyle a(a+4)=0$

En we stellen elke term gelijk aan 0:

$\displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}$

We verkregen 0 en -4 als oplossingen. Daarom, wanneer

$\displaystyle a$

verschillend is van 0 en -4, zal de 3×3-determinant anders zijn dan 0 en daarom zal de rangorde van de matrix 3 zijn.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 0, -4 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=0 :$

$\displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 0 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=-4 :$

$\displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -4 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

We hebben daarom 3 gevallen gevonden waarin het bereik van matrix A varieert afhankelijk van de waarde die de parameter aanneemt:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Oefening 4

Zoek de omvang van de volgende matrix met afmeting 3×4 volgens de waarde van de parameter

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}$

zie oplossing

De matrix A zal hoogstens rang 3 zijn, aangezien we geen 4×4 determinant kunnen berekenen. Daarom moeten we eerst alle mogelijke determinanten van orde 3 oplossen (met de regel van Sarrus), om te zien of deze van orde 3 kunnen zijn:

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}$

De resultaten van alle mogelijke determinanten van orde 3 zijn 0, ongeacht de waarde ervan

$\displaystyle a$

. De matrix zal dus nooit rang 3 hebben, omdat het niet uitmaakt welke waarde deze heeft

$\displaystyle a$

dat er nooit een andere 3×3 determinant dan 0 zal zijn.

Dus nu proberen we determinanten van dimensie 2 × 2. Alle determinanten van orde 2 geven echter ook 0, behalve het volgende:

$\displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}$

Nu stellen we het resultaat gelijk aan 0 en lossen we de vergelijking op:

$\displaystyle 8a+16=0$

$\displaystyle 8a=-16$

$\displaystyle a=\cfrac{-16}{8} =-2$

Daarom, wanneer

$\displaystyle a$

verschillend is van -2, zal de determinant 2×2 verschillend zijn van 0 en daarom zal de rangorde van de matrix 2 zijn.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq -2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Laten we nu eens kijken wat er wanneer gebeurt

$\displaystyle a=-2 :$

$\displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}$

Zoals we eerder zagen, wanneer

$\displaystyle a$

is -2, alle determinanten van orde 2 zijn 0. Deze kan daarom niet van rang 2 zijn. En aangezien er minstens één 1×1 determinant bestaat die verschilt van 0, is in dit geval de rang van de matrix 1:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -2 \ \longrightarrow \ Rg(A)=1} \phantom{33} \\[-2ex] & \end{array} }$

We hebben daarom 2 gevallen gevonden waarin het bereik van matrix A varieert met de waarde die de parameter aanneemt:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }$

Hoe u het bereik van een array kunt berekenen op basis van een parameter. Voorbeeld:

Problemen met op parameters gebaseerde matrixbereiken opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren