Reverse Polish Notation (RPN) is een van de meest voorkomende bewerkingen die een programmeur kan tegenkomen. Deze notatie werd in 1920 geïntroduceerd door de wiskundige Jan Łukasiewicz en werd speciaal ontwikkeld om extreem grote wiskundige uitdrukkingen te reduceren. Bovendien wordt dit type notatie momenteel veel gebruikt in de wereld van wetenschappelijke rekenmachines, dus we raden u aan bij ons te blijven om te leren hoe u het correct kunt gebruiken.
Waar of bij welk type wiskundige bewerking kun je de omgekeerde Poolse notatie tegenkomen?
Dit type wiskundige taal wordt vaak aangetroffen in de rekenkunde en algebra en is een soort operationele taal waarmee elke systeemingenieur goed vertrouwd zou moeten zijn. In de loop van de tijd is dit type numerieke bewerking of expressie beschouwd als een uitstekend alternatief om het geheugengebruik op een computer aanzienlijk te verminderen. En sinds dit werd ontdekt, heeft het gebruik ervan zich naar elk besturingssysteem ter wereld verspreid. Hierdoor kan het snel worden geprogrammeerd, waardoor er een aanzienlijk tijdverlies ontstaat.
In de meeste gevallen heeft een programmeur meer tijd nodig dan verwacht om de werking van een applicatie en besturingssysteem, webpagina, enz. te ontwikkelen. Om de omgekeerde Poolse notatie bij het programmeren toe te passen, moet u werken met de LIFO-structuur (Last in first out) van wiskundige bewerkingen. Dit type procedure is gebaseerd op het feit dat een hele operatie niet op een ordelijke manier hoeft te worden uitgevoerd om het verwachte resultaat te vinden. Het beste is om het uit te leggen met een voorbeeld:
Stel dat we een geautomatiseerde internationale valutawisselpagina moeten programmeren, eerst moeten we alle argumenten plaatsen, in dit geval zullen we werken met de dollar en de euro. In principe zou de bewerking A x B = C kunnen zijn, ervan uitgaande dat A in dollars is en B de waarde van de euro in dollars is.
Bij het uitvoeren van de bewerking zullen we uiteraard de dollars hebben die we nodig hebben om een geschat bedrag van euro’s aan te schaffen, maar bij het programmeren van de pagina moet de bewerking automatisch gebeuren. Dit is de reden waarom de omgekeerde Poolse notatie wordt toegepast, en in dit geval zou deze als volgt worden uitgedrukt: AB x, dus het resultaat, dat C zou zijn, zou automatisch op de pagina worden toegepast.
Hoe kan ik de omgekeerde Poolse notatie correct construeren?
Zoals de naam doet vermoeden, zou een omgekeerde Poolse uitdrukking in wezen de operanden eerst plaatsen (dit zijn de getallen die we moeten delen, vermenigvuldigen, enz.), en vervolgens de operator. De operator in dit geval zou vermenigvuldigen, delen, optellen zijn, naast andere procedures, en natuurlijk kan een eenvoudig voorbeeld dat je in de context houdt nooit kwaad, dus we zullen het hieronder weergeven.
AB+
Stel dat A 15 is en B 45, dan zal het systeem bij het programmeren op deze manier onmiddellijk herkennen dat we het over een wiskundige bewerking hebben en daarom zullen we onmiddellijk c vinden. In dit geval zou dat 65 zijn.
Als je programmeren bestudeert, zal het veel sneller voor je zijn om de volgende code te begrijpen die we hieronder presenteren.
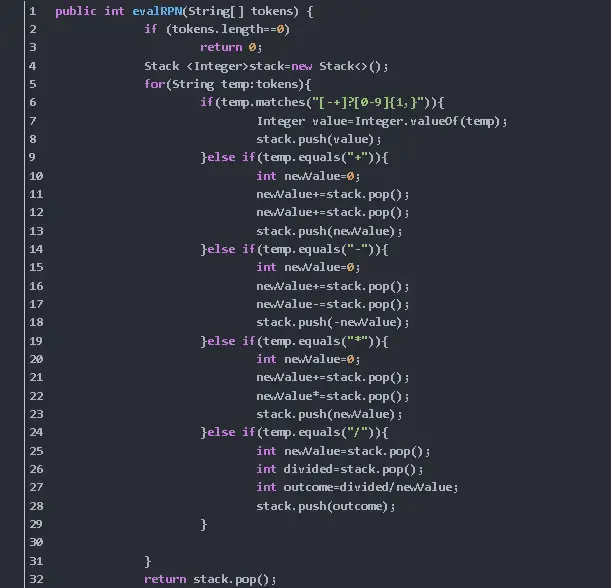
Het presenteert een eenvoudige bewerking die, in omgekeerde Poolse notatie zonder programmering, als volgt zou worden uitgedrukt.
1) [“2”, “1”, “+”, “3”, “*”] -> ((2 + 1) * 3) -> 9
2) [“4”, “13”, “5”, “/”, “+”] -> (4 + (13 / 5)) -> 6
Analyse van de operatie:
Er moet rekening mee worden gehouden dat deze bewerking een stapeling moet zijn, met een bijzondere neiging tot delen en aftrekken. En ten eerste moeten we de splitsing wegwerken, door alle gegevens tussen de eerste haakjes te extraheren. Eenmaal berekend, wordt deze nieuwe waarde op de stapel geplaatst, en natuurlijk zou de hele procedure het getal 6 opleveren, rekening houdend met het feit dat elke bewerking onafhankelijk is van de andere, en we nemen het getal 2 als voorbeeld.
Welke voordelen kan de omgekeerde Poolse notatie u bieden?
- De berekening van elk type wiskundige bewerking dat u wilt uitdrukken, wordt opeenvolgend ontwikkeld, zodat we minder fouten zullen tegenkomen bij het maken van welk type complexe bewerking dan ook.
- Het vereist geen gebruik van haakjes of enige vorm van algebraïsche regel, omdat we informatie toevoegen, dus elke bewerking wordt in stappen berekend.
- Voor studenten programmeren of welk type techniek dan ook, wordt het veel gemakkelijker om de bewerking die wordt uitgevoerd te begrijpen.
- Het kopiëren van elk type wiskundige bewerking rechtstreeks naar een rekenmachine zonder diepgaande kennis van de rekenkunde kan fouten veroorzaken. Daarom is het praktischer om een NPI toe te passen.
- U moet het =-symbool niet gebruiken om het verwachte resultaat te vinden.
Welke rekenmachines worden het meest aanbevolen voor het toepassen van een NPI (Reverse Polish Notation)?
Rekenmachines zijn het beste hulpmiddel voor elke leerling, maar in de meeste gevallen zijn ze alleen ontworpen om eenvoudige bewerkingen uit te voeren en zijn ze op dezelfde manier geconfigureerd als normaal gesproken geschreven. Dus als je op zoek bent naar een rekenmachine die overweg kan met omgekeerde Poolse notatie, dan heb je er een nodig die iets eenvoudiger is, waarbij de meest populaire onder programmeurs de HP 50G is.
Hoewel er ook andere rekenmachines zijn die dit soort bewerkingen online kunnen uitvoeren (veel HP-rekenmachines kunnen een goede optie zijn om te overwegen), maar het hebben van een gespecialiseerde rekenmachine kan het programmeerproces natuurlijk versnellen.
Onder de voordelen kunnen we benadrukken:
- Ingebouwde bibliotheek speciaal voor complexe vergelijkingen.
- Meer dan 300 automatische formules met wetenschappelijke constanten voor elk type bewerking met omgekeerde Poolse notatie.
- Hiermee kun je nog sneller applicaties ontwikkelen dan verwacht.
- Het voldoet ook aan de normen van een gewone wetenschappelijke rekenmachine, dus de omgekeerde Poolse notatie is misschien wel het sterke punt, maar het werkt ook voor andere soorten bewerkingen.
Omgekeerde Poolse notatie heeft de programmeersystemen aanzienlijk gerevolutioneerd. Het wordt zonder twijfel aanbevolen om deze toe te passen om exacte resultaten te verkrijgen, zonder veelvoorkomende rekenfouten. Waar wacht je nog op om de jouwe te krijgen? Ten slotte raden we u aan ons artikel over Wiskundige Notatie te lezen, omdat dit een zeer goede aanvulling kan zijn op de informatie over Reverse Polish Notation (RPN) die u in dit artikel leert.