Op deze pagina vind je de uitleg van nulmatrix, ook wel nulmatrix genoemd. Je zult met voorbeelden ook zien dat de waarden van de elementen onafhankelijk zijn van de dimensie van de matrix, en tot slot zul je alle eigenschappen van dit type matrix vinden.
Wat is de nulmatrix?
De nulmatrix (of nulmatrix) is een matrix waarvan de elementen allemaal gelijk zijn aan nul (0).
Daarom kan deze matrix, volgens de definitie van een nulmatrix, alle mogelijke dimensies hebben, zolang alle getallen nul zijn. Kijk naar de volgende voorbeelden:
Voorbeelden van nulmatrices
Voorbeeld van 2 × 2 nulmatrix
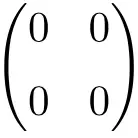
Voorbeeld van 3 x 3 nulmatrix
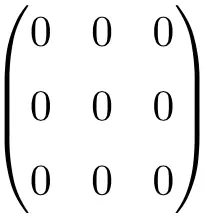
Voorbeeld van een 4 × 4 nulmatrix
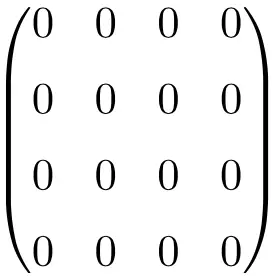
Het lijkt je nu misschien dat deze zeer specifieke matrix er niet toe doet, omdat het eenvoudigweg een matrix vol nullen is. In de wiskunde, meer specifiek op het gebied van lineaire algebra, is het echter een zeer nuttige matrix omdat het berekeningen veel eenvoudiger maakt.
Eigenschappen van nulmatrix
Nul- (of nul-) matrices hebben de volgende kenmerken:
- De nulmatrix is het neutrale element van de matrixoptelling, daarom:
![]()
- Matrixvermenigvuldiging heeft de multiplicatieve eigenschap van nul, dat wil zeggen dat het product van elke matrix vermenigvuldigd met de nulmatrix gelijk is aan 0.
![]()
- Als de matrix vierkant is, is de nulmatrix zowel symmetrisch als antisymmetrisch .
- De nulmatrix is de enige matrix waarvan de rang nul is.
- De determinant van de nulmatrix evalueert altijd naar 0, dus dit type matrix heeft geen inverse (het is een enkelvoudige matrix).
- Uiteraard is de nulmatrix een voorbeeld van een nilpotente matrix .