▷ Nul-onbepaaldheid tussen nul oplossen (0/0)

In dit artikel leggen we uit hoe je de limiet van een functie kunt opslaan als deze de onzekerheid 0/0 geeft. Daarnaast kun je oefenen met opgeloste oefeningen op de onbepaaldheid van nul tussen nul.

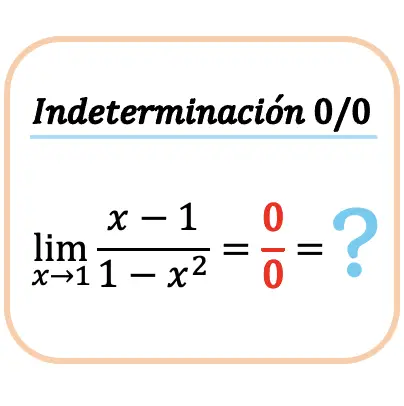
Hoe nul-onbepaaldheid tussen nul (0/0) op te lossen

We zullen dan zien hoe we de limiet van een functie kunnen berekenen wanneer deze een onbepaaldheid nul geeft tussen nul (0/0). Om dit te doen, zullen we stap voor stap een voorbeeld berekenen:

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

We proberen eerst de limiet te berekenen door de waarde van x in de functie te vervangen:

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

Maar we verkrijgen de onbepaaldheid 0 gedeeld door 0.

Wanneer de limiet van een puntfunctie de onzekerheid 0/0 geeft, is het noodzakelijk om de polynomen van de teller en de noemer in factoren te ontbinden en vervolgens de gemeenschappelijke factoren te vereenvoudigen.

We moeten daarom de polynomen van de teller en de noemer van de breuk ontbinden in factoren. Om dit te doen, gebruiken we de regel van Ruffini:

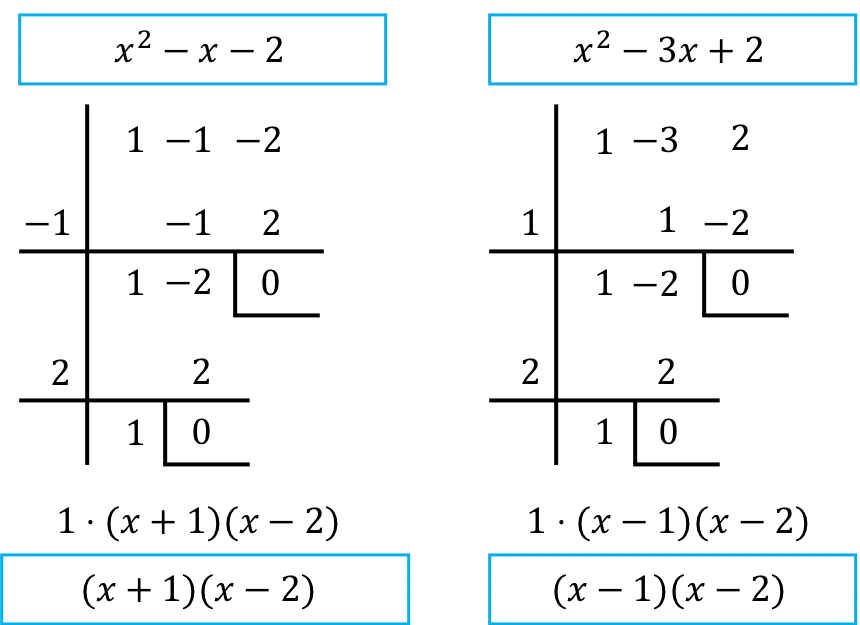
➤ Als je niet weet hoe je een polynoom moet ontbinden , raden we je aan de uitleg te bekijken op onze site gespecialiseerd in polynomen: www.polinomios.org

Dus zodra de polynomen in factoren zijn verwerkt, is de limiet als volgt:

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

We kunnen nu de limiet vereenvoudigen door de factoren te elimineren die zich herhalen in de teller en de noemer van de breuk:

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

En ten slotte herberekenen we de limiet:

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

Zoals je kunt zien, is het, zodra we de polynomen ontbinden en vereenvoudigen, heel gemakkelijk om de oplossing in de limiet te vinden.

Onbepaaldheid 0/0 met wortels

We hebben zojuist gezien hoe de 0/0 onbepaaldheid van rationale functies wordt opgelost. Als de limiet echter een irrationele (of radicale) functie heeft, wordt de 0/0-onbepaaldheid anders opgelost.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

Eerst proberen we de limiet op te lossen door de volgende bewerkingen uit te voeren:

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

Maar we krijgen nul boven nul onbepaaldheid.

Als de limiet van een functie met wortels de onbepaaldheid 0/0 oplevert , moet je de teller en de noemer van de breuk vermenigvuldigen met de conjugaat van de worteluitdrukking.

➤ Onthoud dat de conjugaat dezelfde irrationele uitdrukking is, maar met een aangepast middelste teken.

Vervolgens vermenigvuldigen we zowel de teller als de noemer van de breuk met het conjugaat van de worteluitdrukking:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

Binnen dit soort grenzen zullen we door deze stap te doen altijd een opmerkelijke identiteit verkrijgen die we kunnen vereenvoudigen. In dit geval hebben we in de noemer het product van een som en een verschil, dus:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

We vereenvoudigen de factor die wordt herhaald in de teller en de noemer:

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

En op deze manier kunnen we het resultaat van de limiet vinden:

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

Opgeloste oefeningen over onbepaaldheid 0/0

Hieronder hebben we verschillende stapsgewijze opgeloste oefeningen voorbereid over de limieten van functies die 0/0 onbepaaldheid opleveren. U kunt proberen ze uit te voeren en vervolgens de oplossing controleren.

Vergeet niet dat je ons in de reacties al je vragen over het oplossen van limieten kunt stellen!

Oefening 1

Bereken de limiet van de volgende rationale functie op het punt x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Zie de oplossing

Logischerwijs proberen we eerst de limiet op te lossen:

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Maar we eindigen met 0/0 onbepaaldheid. We moeten daarom de polynomen van de teller en de noemer ontbinden in factoren:

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Nu vereenvoudigen we de breuk door de haakjes te verwijderen die herhaald worden in de teller en de noemer:

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

En ten slotte herberekenen we de limiet met de vereenvoudigde breuk:

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Oefening 2

Los de limiet van de volgende functie op als x -1 nadert:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Zie de oplossing

We proberen eerst de limiet op te lossen zoals gewoonlijk:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Maar we verkrijgen de onbepaaldheid 0 tussen 0. We moeten daarom de 2 polynomen van de breuk ontbinden:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

We kunnen nu de polynomen vereenvoudigen:

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

En we lossen de limiet op:

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Oefening 3

Bepaal de oplossing van de limiet van de volgende radicale functie:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Zie de oplossing

Eerst controleren we of de limiet enige vorm van onbepaaldheid geeft:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

De limiet geeft de onbepaaldheid nul gedeeld door nul en we hebben een wortel in de functie. We moeten daarom de teller en de noemer van de breuk vermenigvuldigen met de conjugaat van de worteluitdrukking:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

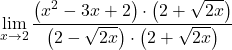
De noemer komt overeen met de ontwikkeling van de opmerkelijke identiteit van het product van een som en een verschil, we kunnen het daarom vereenvoudigen:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

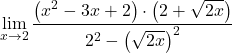
We kunnen de voorwaarden van de breuk echter nog niet vereenvoudigen. We moeten daarom de polynomen in factoren ontbinden:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

Op deze manier kunnen we de breuk vereenvoudigen:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

En nu kunnen we het resultaat van de limiet bepalen:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Oefening 4

Bereken de limiet als x 0 nadert van de volgende radicale functie:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Zie de oplossing

Eerst proberen we de limiet van de functie te berekenen zoals we altijd doen:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Maar we krijgen de onbepaalde vorm van 0/0. Daarom vermenigvuldigen we de teller en de noemer van de functie met de conjugaat van de irrationele uitdrukking:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

We passen de overeenkomstige opmerkelijke identiteitsformule toe om de noemer te vereenvoudigen:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

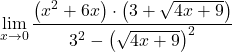
Nu ontbinden we de binomiaal van de teller door de gemeenschappelijke factor te nemen:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

We vereenvoudigen de factoren die worden herhaald in de teller en de noemer van de functie:

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

En ten slotte lossen we de limiet van de functie op:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Oefening 5

Los de volgende limiet op met behulp van de 0/0 onbepaaldheidsmethode:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ Zie: hoe bereken je de laterale grenzen van een functie

Zie de oplossing

We proberen eerst de limiet op te lossen:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Maar in de limiet verkrijgen we nul-op-nul onbepaaldheid. Daarom ontbinden we de polynomen van de teller en de noemer in factoren:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Nu vereenvoudigen we de breuk door de factoren te elimineren die zich herhalen in de teller en de noemer:

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

En we berekenen de limiet opnieuw:

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Maar nu bevinden we ons met de onbepaaldheid van een getal gedeeld door 0. We moeten daarom de laterale grenzen van de functie berekenen wanneer x naar -1 neigt.

We lossen eerst de laterale limiet van de functie op in het punt x=-1 aan de linkerkant:

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

En dan berekenen we de laterale limiet van de functie op het punt x=-1 aan de rechterkant:

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Omdat de twee laterale limieten niet samenvallen, bestaat de limiet van de functie op x = -1 niet:

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Nul onbepaaldheid tussen nul (0/0)

Hoe nul-onbepaaldheid tussen nul (0/0) op te lossen

Onbepaaldheid 0/0 met wortels

Opgeloste oefeningen over onbepaaldheid 0/0

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren