In dit artikel leggen we uit hoe je de monotoniciteit van een functie kunt kennen, dat wil zeggen hoe je de intervallen van toename en afname van een functie kunt vinden. Daarnaast kun je met stapsgewijze oefeningen oefenen op de groei en achteruitgang van een functie.
Wat is de monotoniciteit van een functie?
Een functie is monotoon op een interval als deze de gegeven volgorde behoudt. Er zijn vijf soorten monotonie:
- Monotoon toenemende functie: wanneer de waarde van de functie op een bepaald punt altijd gelijk is aan of groter is dan de waarde van de functie op een vorig punt.
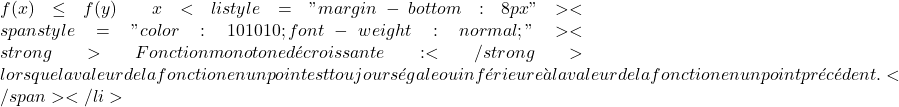 Strikt monotoon toenemende functie: wanneer de waarde van de functie op een bepaald punt altijd groter is dan de waarde van de functie op een vorig punt.
Strikt monotoon toenemende functie: wanneer de waarde van de functie op een bepaald punt altijd groter is dan de waarde van de functie op een vorig punt.
 Constante functie wanneer de waarde van de functie op een bepaald punt altijd gelijk is aan de waarde van de functie op een vorig punt.
Constante functie wanneer de waarde van de functie op een bepaald punt altijd gelijk is aan de waarde van de functie op een vorig punt.

![]()
x^2-4=0x^2=4x=\pm 2
![]()
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
![]()
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
![]()
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
![]()
\links(x^2-4\rechts)^2}
![]()
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
![]()
f'(x)=0,



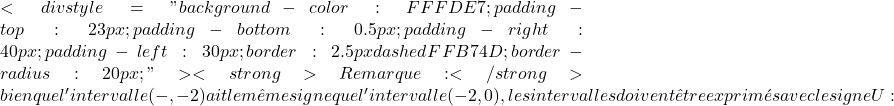
![]()
(-\infty,0)

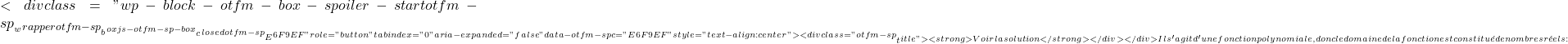
![]()
f'(x)=0.
![]()
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
![]()
f'(x)= 03x^2-12x+9=0\begin{uitgelijnd}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{cases} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{cases} \end{uitgelijnd}
![]()
f'(x)=0
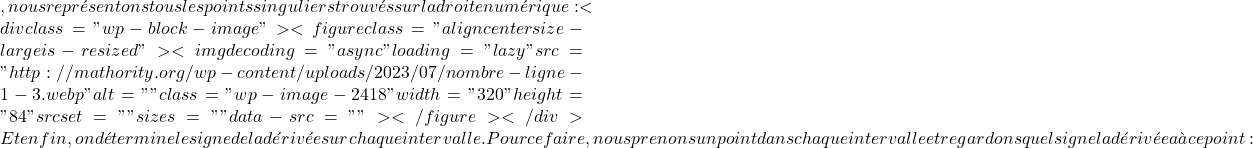


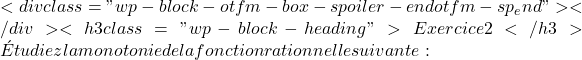
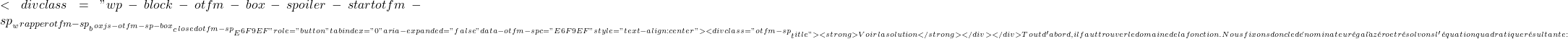
![]()
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
![]()
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ links(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
![]()
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
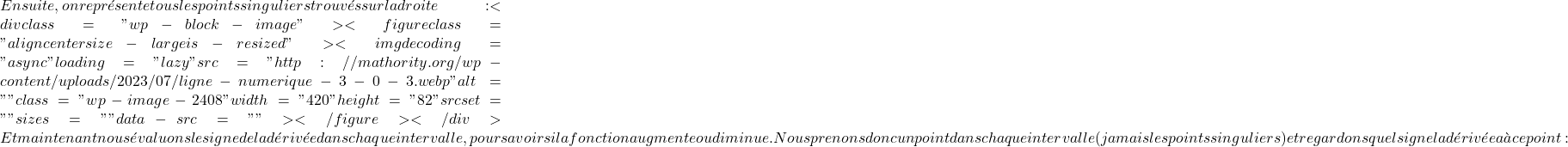


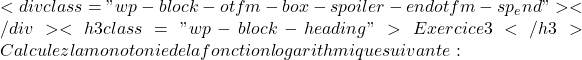
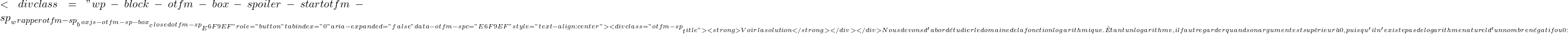
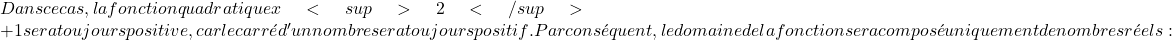
![]()
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
![]()
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0


