Hier leggen we alles uit wat u moet weten over monomials: wat ze zijn, wat hun onderdelen zijn (en hoe u ze kunt identificeren), de verschillende soorten monomials, hoe u bewerkingen met monomials kunt berekenen, de numerieke waarde van een monomial. .. Daarnaast kun je voorbeelden en oefeningen zien die stap voor stap zijn opgelost met monomials.
Wat zijn monomieën?
In de wiskunde is de definitie van een monomial als volgt:
Een monomial is een algebraïsche uitdrukking die wordt gevormd door een combinatie van cijfers en letters. Preciezer gezegd, een monomial bestaat uit het product tussen een getal en een of meer variabelen (letters) verheven tot exponenten.
De term 7x 3 y 2 wordt bijvoorbeeld een monomiaal genoemd omdat deze een getal (7) en verschillende letters (x, y) heeft.
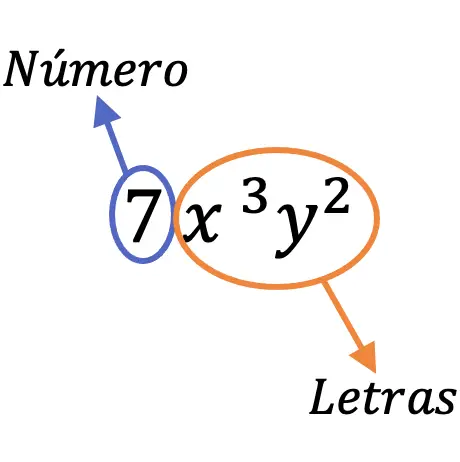
Delen van een monomiaal
Nu we de betekenis van een monomial hebben gezien, gaan we kijken wat alle onderdelen van een monomial zijn:
- Coëfficiënt : is het getal dat de variabelen (of letters) van de monomial vermenigvuldigt.
- Variabel : is elk van de letters die in de monomial voorkomen.
- Letterlijk deel : komt overeen met alle variabelen waaruit de monomial bestaat, met al hun respectieve exponenten.
- Graad : bestaat uit de som van alle exponenten van de letters die de monomiaal vormen.
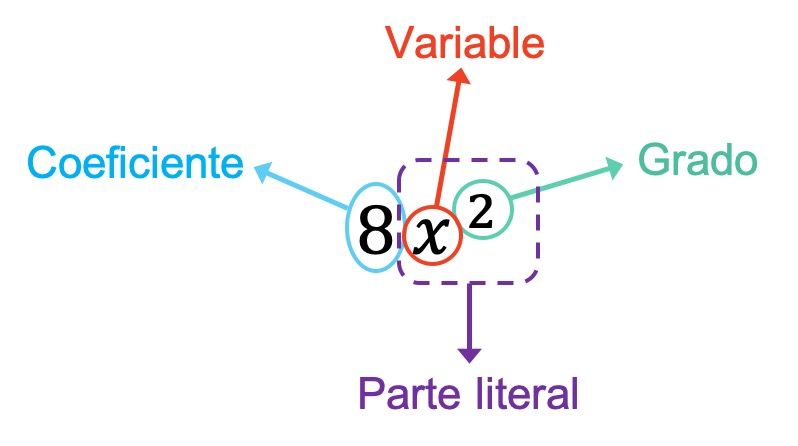
De coëfficiënt van de monomial in het bovenstaande voorbeeld is 8, omdat dit het getal is dat de variabelen vermenigvuldigt. Ook in dit geval heeft de monomial slechts één variabele, namelijk x. Het letterlijke deel van de monomial wordt dus gevormd door deze variabele plus zijn exponent, namelijk x 2 . Ten slotte is de graad van de monomial 2 omdat dit de enige exponent is die deze heeft.
Probeer nu de volgende oefening op de delen van een monomiaal op te lossen:
- Identificeer alle delen van de volgende monomial:
![]()
De componenten van de monomial van de verklaring zijn:
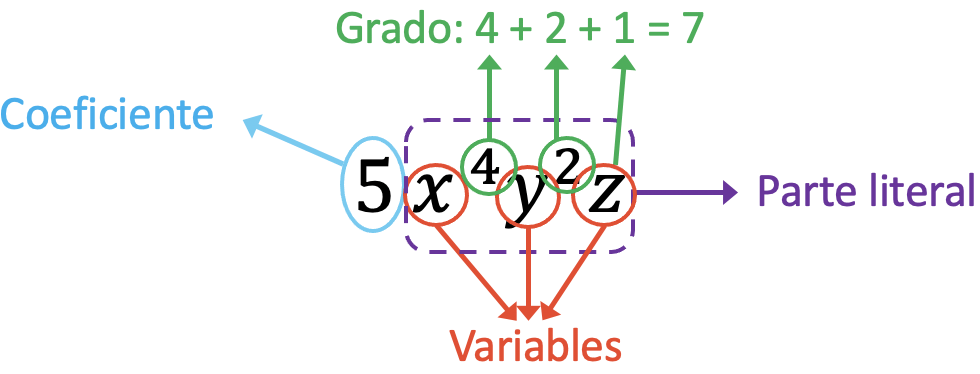
De coëfficiënt van de monomial in het probleem is 5, omdat het de term is die de letters vermenigvuldigt. Aan de andere kant zijn de variabelen van deze monomial x, y, z. Ten derde komt het letterlijke deel van de monomial overeen met de uitdrukking x 4 y 2 z. En ten slotte is de graad van de monomiaal gelijk aan de som van alle exponenten van de variabelen, dat wil zeggen 7 (4+2+1=7).
Merk op dat wanneer een letter geen exponent heeft, dit feitelijk betekent dat hij een 1 als exponent heeft. Om de graad van de monomial van het probleem te berekenen, voegen we daarom een eenheid toe die de exponent van de variabele z vertegenwoordigt.
Soorten monomialen
Er zijn verschillende soorten monomials, elk met hun eigen eigenschappen. De belangrijkste monomialen zijn gelijksoortige monomialen, homogene monomialen, heterogene monomialen en tegengestelde monomialen. Vervolgens zullen we de kenmerken van elk type zien.
vergelijkbare monomieën
Soortgelijke monomials zijn monomials die hetzelfde letterlijke deel hebben. Daarom zijn twee of meer monomialen vergelijkbaar als ze dezelfde letters en exponenten hebben.
De volgende twee monomialen zijn bijvoorbeeld vergelijkbaar omdat ze, hoewel ze verschillende coëfficiënten hebben, door dezelfde variabelen worden gevormd en tot dezelfde exponenten worden verheven.
![]()
Zoals we later zullen zien, wordt dit type monomials gebruikt om bewerkingen op monomials op te lossen.
homogene monomieën
Twee monomialen zijn homogeen als hun absolute graad gelijk is.
De volgende twee monomialen zijn bijvoorbeeld homogeen omdat de graad van beide gelijk is aan 5:
![]()
De eerste monomial heeft een enkele variabele die wordt verheven tot de macht 5, dus de graad is 5. En de tweede polynoom heeft één variabele in het kwadraat en een andere in de derde macht, dus de graad is ook 5 (2+ 3 =5).
Zoals je kunt zien, hoeven twee monomialen, om homogeen te zijn, niet hetzelfde letterlijke deel te hebben, maar alleen dezelfde absolute graad.
heterogene monomieën
Heterogene monomialen zijn monomialen die niet dezelfde absolute graad hebben. Met andere woorden: heterogene monomialen zijn het tegenovergestelde van homogene monomialen.
De volgende 3 monomialen zijn heterogeen omdat ze elk een andere graad hebben:
![]()
De eerste monomial is van graad 8, de tweede monomial is van graad 2 en de derde monomial is van graad 11. Daarom zijn de drie monomialen heterogeen ten opzichte van elkaar.
Tegenover monomialen
Tegengestelde monomialen zijn monomialen die homogeen zijn (hetzelfde letterlijke deel hebben) en bovendien zijn hun coëfficiënten tegengesteld, dat wil zeggen dat hun coëfficiënten dezelfde waarde hebben maar een tegengesteld teken.
De volgende twee monomialen zijn bijvoorbeeld tegenpolen:
![]()
De twee voorgaande monomialen zijn tegengestelden omdat ze alleen verschillen in hun teken, de eerste heeft een positief teken en de tweede een negatief teken.
Nu je verschillende voorbeelden van monomialen hebt gezien, ben je misschien geïnteresseerd in een andere soortgelijke algebraïsche uitdrukking: de binominale . In feite bestaat een binomiaal uit de optelling (of aftrekking) van verschillende monomialen, dus het is interessant om de relatie tussen deze twee concepten te zien. U kunt zien wat de betekenis van binomiaal is door op deze link te klikken.
Operaties met monomials
Om het concept van monomials te verdiepen, zullen we zien welke bewerkingen met monomials kunnen worden uitgevoerd. In het bijzonder kunnen monomialen worden opgeteld, afgetrokken, vermenigvuldigd, verdeeld en macht. En elk type operatie heeft zijn eigenaardigheden, dus we zullen ze hieronder één voor één afzonderlijk analyseren.
som van monomialen
Er kunnen alleen twee of meer monomialen worden toegevoegd als het vergelijkbare monomialen zijn. Vervolgens is de som van twee vergelijkbare monomialen gelijk aan een andere monomial die bestaat uit hetzelfde letterlijke deel en de som van de coëfficiënten van deze twee monomialen.

Voorbeelden van sommen van monomialen
Als je wilt oefenen met het maken van monomiale opteloefeningen, kun je deze opzoeken in de zoekmachine rechtsboven, want we hebben een hele pagina vol met opgeloste monomiale opteloefeningen.
aftrekken van monomialen
Twee of meer monomialen kunnen alleen van elkaar worden afgetrokken als het vergelijkbare monomialen zijn. De aftrekking van twee soortgelijke monomialen is dus gelijk aan een andere monomial die uit hetzelfde letterlijke deel bestaat, en de aftrekking van de coëfficiënten van deze twee monomialen.

Voorbeelden van het aftrekken van monomialen
Je kunt oefenen met de opgeloste stapsgewijze monomiale aftrekkingsoefeningen die op onze website te vinden zijn. Je kunt ze vinden via de zoekmachine rechtsboven.
vermenigvuldiging van monomialen
Het resultaat van de vermenigvuldiging van twee monomialen is een andere monomial waarvan de coëfficiënt het product is van de coëfficiënten van de monomialen en waarvan het letterlijke deel wordt verkregen door de variabelen die dezelfde basis hebben te vermenigvuldigen, dat wil zeggen door hun exposanten op te tellen.

Om het product tussen twee verschillende monomialen op te lossen, moeten de coëfficiënten dus met elkaar worden vermenigvuldigd en moeten de exponenten van machten met hetzelfde grondtal worden opgeteld.
Aan de andere kant, als we twee monomialen met verschillende basismachten vermenigvuldigen, moeten we eenvoudigweg hun coëfficiënten met elkaar vermenigvuldigen en de machten hetzelfde laten:
![]()
Voorbeelden van vermenigvuldiging van monomials
Om te oefenen met opgeloste stapsgewijze oefeningen voor het vermenigvuldigen van monomialen, kunt u het artikel raadplegen dat we op deze site hebben. Je vindt het gemakkelijk met de zoekmachine rechtsboven.
verdeling van monomialen
Het resultaat van de deling van monomialen is een ander monomial waarvan de coëfficiënt gelijk is aan het quotiënt van de coëfficiënten van de monomialen en waarvan het letterlijke deel wordt verkregen door de variabelen te delen die dezelfde basis hebben, dat wil zeggen door hun exposanten af te trekken.

Dus om twee verschillende monomialen te verdelen, verdelen we eenvoudigweg de coëfficiënten ertussen en trekken we de exponenten af van de machten die dezelfde basis hebben.
Voorbeelden van de verdeling van monomials
Het delen van monomialen is moeilijker dan het lijkt, dus we raden je aan om stap voor stap de opgeloste oefeningen uit te voeren die we hebben over het delen van monomialen . De snelste manier om ze te vinden is via onze zoekmachine rechtsboven.
kracht van een monomiaal
Om de macht van een monomial te berekenen, moet elk element van de monomial worden verheven tot de machtsexponent . Met andere woorden, de macht van een monomial bestaat uit het verhogen van de coëfficiënt en de variabelen (letters) ervan tot de exponent van de macht.

Onthoud uit de eigenschappen van machten dat wanneer we een term verhogen die al verhoogd is, de twee exponenten met elkaar worden vermenigvuldigd. Om deze reden wordt in de macht van een monomiaal de exponent van elke letter altijd vermenigvuldigd met de exponent die de macht aangeeft .
Voorbeelden van bevoegdheden van monomials
Het is vrij gemakkelijk om een fout te maken bij dit soort operaties met monomials. Daarom raden wij je aan om te oefenen met de oefeningen die we stap voor stap op onze website hebben opgelost . Je vindt ze snel door ze op te zoeken in de zoekmachine rechtsboven.
Numerieke waarde van een monomial
De numerieke waarde van een monomial is het resultaat dat wordt verkregen door de variabelen van een monomial te vervangen door bepaalde waarden.
Als we bijvoorbeeld de volgende monomiaal hebben:
![]()
Als we de numerieke waarde van de vorige monomial voor willen vinden
![]()
je moet de letter vervangen
![]()
van de monomial met 2 en los de resulterende bewerkingen op:
![]()
Dus de numerieke waarde van de monomiaal
![]()
Voor
![]()
is gelijk aan 20.
U kunt ook de numerieke waarde van een monomiale multivariabele bepalen. Als we bijvoorbeeld de volgende bivariabele, of met andere woorden, monomial met twee variabelen hebben:
![]()
Om de numerieke waarde van het bovenstaande monomiaal te berekenen wanneer
![]()
ter waarde van 1 e
![]()
is -2, vervangen we de letters door hun respectievelijke waarden:
![]()
Dus de numerieke waarde van de monomial van het probleem voor
![]()
En
![]()
retourneert -6.
Monomialen en polynomen
Weet ten slotte dat polynomen kunnen worden gevormd uit monomialen:
Een polynoom is de groepering van twee of meer monomialen.
![]()
Het vorige polynoom is bijvoorbeeld het resultaat van de optelling (of aftrekking) van 3 heterogene monomialen.
Uit nieuwsgierigheid: als een polynoom slechts twee monomialen heeft, wordt het een binomiaal genoemd. En als een polynoom precies 3 monomialen heeft, wordt het een trinomiaal genoemd.
Als u meer wilt weten over polynomen, kunt u de hoofdpagina van internet bezoeken, waar we alles uitleggen wat u moet weten over polynomen.