Nilpotente matrix - Mathority

Op deze pagina vindt u uitleg over wat een nilpotente matrix is, evenals verschillende voorbeelden, zodat u het kunt begrijpen en geen twijfels kunt hebben. Bovendien kunt u de structuren van nilpotente matrices en alle eigenschappen van dit soort matrices zien.

Wat is een nilpotente matrix?

De definitie van nilpotente matrix is als volgt:

Een nilpotente matrix is een vierkante matrix die tot een geheel getal de nulmatrix oplevert.

$N^k =0$

Goud

$N$

is de nilpotente matrix en

$k$

de exponent van de macht die de nulmatrix geeft.

Deze voorwaarde betekent niet dat de macht van een nilpotente matrix altijd nul oplevert, ongeacht de exponent, maar eerder dat als er ten minste één macht van de matrix bestaat waarvan het resultaat een matrix vol nullen is, de matrix nilpotent is.

Aan de andere kant is de nilpotentie-index van een nilpotente matrix het kleinste getal waarmee aan de nilpotentie-voorwaarde wordt voldaan. We kunnen ook zeggen dat de nilpotente matrix van orde k is, waarbij k de nilpotentie-index is.

Voorbeelden van nilpotente matrices

Om het begrip van een nilpotente matrix te voltooien, zullen we verschillende voorbeelden van dit type matrix zien:

Voorbeeld van een 2 × 2 nilpotente matrix

De volgende vierkante matrix met afmeting 2×2 is nilpotent:

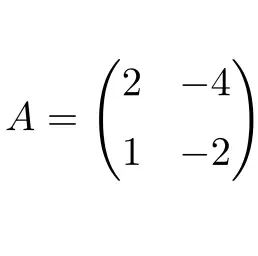
voorbeeld van een nilpotente matrix met dimensie 2x2

De matrix is nilpotent omdat we door het kwadrateren van matrix A de nulmatrix als resultaat krijgen:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

Het is daarom een nilpotente matrix en de nilpotentie-index is 2, aangezien de nulmatrix tot de tweede macht wordt verkregen.

Voorbeeld van een 3×3 nilpotente matrix

De volgende vierkante matrix van orde 3 is nilpotent:

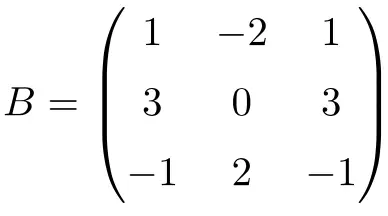
voorbeeld van een nilpotente matrix met dimensie 3x3

Hoewel we door de matrix naar 2 te verhogen niet de nulmatrix krijgen:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Maar bij het berekenen van de kubus van de matrix krijgen we een matrix waarvan alle elementen gelijk zijn aan 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Matrix B is dus een nilpotente matrix, en aangezien de nulmatrix wordt verkregen tot de macht 3, is de nilpotentie-index 3.

Structuur van een 2 × 2 nilpotente matrix

Hieronder zie je de structuur van alle nilpotente matrices. Het bewijs ervan is een beetje vervelend, dus we hebben je direct de formule gegeven om een nilpotente matrix van orde 2 te verkrijgen:

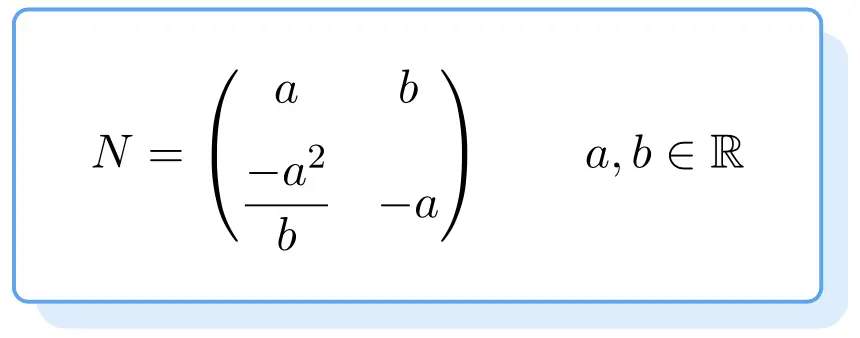
structuur en formule van een 2x2 nilpotente matrix

Dus elke matrix die aan de bovenstaande formule voldoet, zal een nilpotente matrix zijn. Hiervoor de waarden

$a$

$b$

ze kunnen willekeurig zijn, zolang het maar reële getallen zijn.

Eigenschappen van nilpotente matrices

Nilpotente matrices hebben de volgende kenmerken:

Het spoor van een nilpotente matrix is altijd nul.

Op dezelfde manier is de determinant van elke nilpotente matrix altijd 0. Het omgekeerde is echter niet waar, dwz dat de determinant van een matrix nul is, betekent niet dat de matrix nilpotent is.

De enige nilpotente matrix die gediagonaliseerd kan worden, is de nulmatrix.

De nilpotentie-index van een nilpotente matrix met dimensie n×n is altijd gelijk aan of kleiner dan n . Dit is de reden waarom de nilpotentie-index van een 2 × 2 nilpotente matrix altijd 2 zal zijn.

Een nilpotente matrix is niet inverteerbaar.

Elke driehoekige matrix met nullen op de hoofddiagonaal is ook een nilpotente matrix.

Er is een stelling die zegt dat als de matrix
$N$

nilpotent is, dan is de matrix

$N+I$

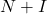
is omkeerbaar, waar

$I$

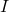
is de identiteitsmatrix. Bovendien kan de inverse matrix worden gevonden met de volgende formule:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Evenzo, als
$N$

een nilpotente matrix is, kan de inverse van de matrix worden berekend

$N-I$

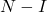
met de volgende vergelijking:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Elke singuliere matrix, dat wil zeggen niet-inverteerbaar, kan worden ontleed in het product van nilpotente matrices.

Alle eigenwaarden (of eigenwaarden) van een nilpotente matrix zijn nul.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Ten slotte is er, als curiositeit, ook het concept van nilpotente transformatie, dat een lineaire toepassing definieert
$L$

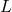
van een vectorruimte zodanig dat

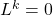
$L^k=0$

.