Magic Squares is een wiskundepuzzelspel dat onze rekenvaardigheden op een leuke en opwindende manier traint. Daarom is het een van de beste hulpmiddelen voor het onderwijzen van wiskunde aan jonge studenten.
Wat is een magische array en hoe wordt deze opgelost?
Een magisch vierkant is een soort tabel of matrix die bestaat uit verschillende vakken, waarin gehele getallen worden geschreven. Maar ze kunnen onder geen enkele omstandigheid worden geïnstalleerd; een reeks regels moet worden gerespecteerd:
- Alle magische sommen (sommen van alle waarden van elke horizontale, verticale of diagonale lijn) moeten altijd de waarde opleveren die gelijkwaardig is aan de magische constante (het is een enkele waarde).
- Geen enkel getal kan tweemaal worden herhaald.
- U kunt alleen opeenvolgende getallen gebruiken (bijvoorbeeld van 1 tot en met 9) of getallen die een bepaalde reeks volgen, bijvoorbeeld: oneven getallen, veelvouden van 5, onder andere.
Het is ook belangrijk om te benadrukken dat we verschillende classificaties van vierkanten kunnen maken, afhankelijk van hun structuur. De eerste is afhankelijk van de graad van het vierkant , wat overeenkomt met het aantal cellen in een rij of kolom. En de tweede is afhankelijk van het type graad van de tafel ( even getallen of oneven getallen). Op basis van dit onderscheid kunnen we alle vierkanten in verschillende categorieën indelen, hoewel we dit later in detail zullen beschrijven.
Hoe magische vierkanten op te lossen?
Om dit wiskundespel op te lossen, kunnen we twee verschillende methoden gebruiken: gebruik geometrie of bereken de magische constante. Beide procedures zijn even geldig, hoewel u met de ene sneller het resultaat kunt bereiken, terwijl de andere meer tijd en redenering vereist. Vervolgens leggen we beide methoden uit, zodat u degene kunt kiezen die u verkiest en u zich beter aan elke situatie kunt aanpassen.
Wat is de formule voor magische vierkanten?
De eerste methode bestaat uit het berekenen van de magische constante , waarvoor we de volgende formule moeten gebruiken: n(n 2 +1)/2, waarbij n de graad van het kwadraat is. En zodra we deze waarde hebben, hoeven we alleen nog maar de verschillende combinaties van getallen uit te proberen, waardoor we de magische sommen van het hele kwadraat gelijk kunnen stellen aan de constante. Met andere woorden: we moeten combinaties van getallen vormen die opgeteld de waarde van de constante vormen, zodat het hele plaatje in balans is.
Hoe magische vierkanten op te lossen met behulp van geometrie?
Ten tweede kunnen we magische vierkanten oplossen met behulp van geometrie . Hoewel moet worden opgemerkt dat deze methode heel eenvoudig is en dat u geen rekenvaardigheden hoeft te oefenen, omdat deze puur methodisch is. Dat gezegd hebbende, zullen we de procedure uitleggen voor zowel het oplossen van vierkanten van de even orde als de vierkanten van de oneven orde.
Hoe los je magische vierkanten met oneven getallen op?
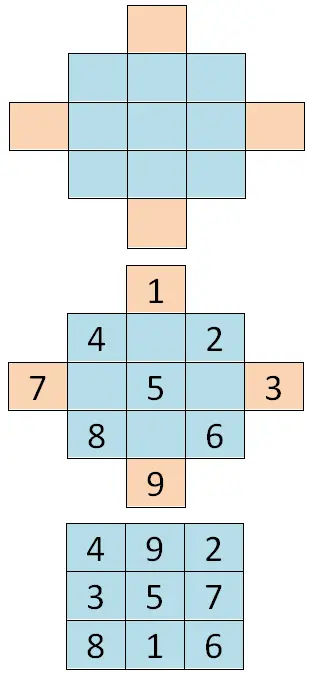
Om dit eerste geval op te lossen, moet u cellen aan de begintabel toevoegen, zodat u een soort ruit krijgt. Vervolgens moeten we alle opeenvolgende getallen schrijven, beginnend met het eerste cijfer van de reeks (in ons geval 1) en volgen we de diagonalen van de ruit . Ten slotte moeten we het cijfer “verdubbelen”, daarom gaan de waarden van de buitenste cellen naar de andere kant. Dus de buitenste cellen van de verticale as snijden elkaar, dan gebeurt hetzelfde met de cellen van de horizontale as, hieronder zie je een voorbeeld:
Hoe los je magische vierkanten van gelijke orde op?
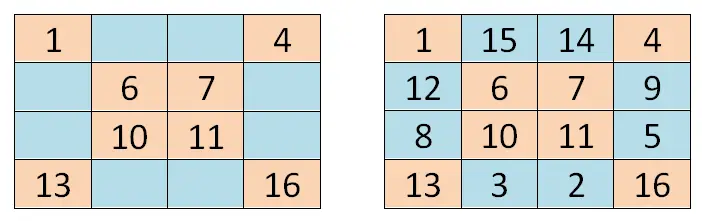
Om een magisch vierkant van gelijke orde op te lossen (magische vierkanten die een even aantal rijen en kolommen hebben), kunnen we onze toevlucht nemen tot een methode die enigszins verschilt van de vorige, maar die ook gebaseerd is op geometrie. We beginnen met het schrijven van het eerste nummer van de reeks (in ons geval 1) in de linkerbovenhoek. Vervolgens doorkruisen we de twee hoofddiagonalen en schrijven we de waarden die overeenkomen met de positie van elk vak.
Zodra we de twee hoofddiagonalen hebben geschreven, moeten we onszelf in het eerste lege vak plaatsen, beginnend vanuit de rechter benedenhoek (vak 15 in ons geval). Daar zullen we de tweede waarde van de reeks schrijven en we zullen de resterende waarden in volgorde schrijven (van klein naar groot), waarbij we de cellen van rechts naar links en van onder naar boven invullen. Om het duidelijker te maken, kunt u zich oriënteren met de afbeelding die we u hieronder laten zien:
Hoe magische vierkanten bouwen?
Om zelf magische vierkanten te bouwen kunnen we verschillende procedures volgen, waarvan we er twee uitlichten. Opgemerkt moet worden dat elk ervan zal worden gebruikt om vierkanten van verschillende typen te maken, dus u zult de methode zorgvuldig moeten kiezen, afhankelijk van het vierkant dat u wilt genereren:
Siamese methode
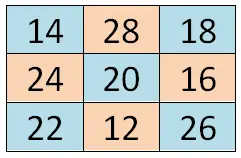
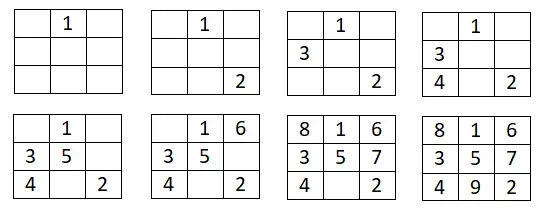
Deze eerste methode is vrij eenvoudig en helpt ons specifiek om vreemde magische vierkanten van elke grootte te construeren. De te volgen procedure is heel eenvoudig. In principe schrijven we het eerste nummer van de reeks in het centrale vak van de eerste rij. Van daaruit gaan we terug in volgorde in de rekenkundige progressie die we hebben gekozen, waarbij we het volgende getal naar boven en naar rechts schrijven. Als deze positie echter buiten het getekende vierkant ligt, zullen we naar de laatste rij of kolom moeten gaan. En als we eindigen met een vol vierkant, zullen we één vakje naar beneden moeten gaan vanaf het laatste getallenveld dat we binnenkwamen en dan gaan we op dezelfde manier verder.
Hieronder zie je een voorbeeld van 3×3:
Strachey’s methode voor magische vierkanten
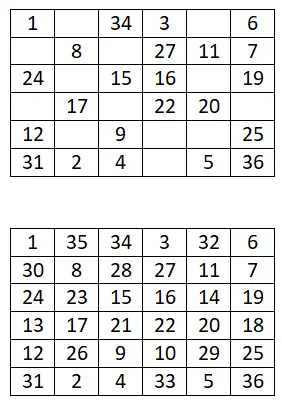
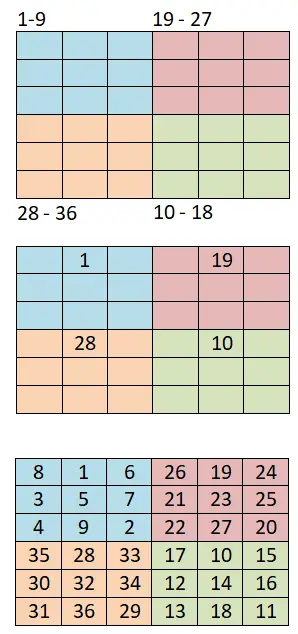
Om magische vierkanten van de orde 4k + 2 paren te genereren, zullen we deze andere methode gebruiken, die gebaseerd is op de vorige (de Siamese methode) en die ook heel eenvoudig is. Hieronder ziet u de te volgen stappen en een uitgewerkt voorbeeld van een 6×6 magisch vierkant:
- Verdelen in kleinere kwadranten: Het eerste wat we moeten doen is het bord in kleinere vierkanten verdelen. Als we bijvoorbeeld een bord van 6×6 hebben, moeten we vier gelijke kwadranten van 3×3 vierkanten maken.
- Gebruik de Siamese methode: dan wijzen we een reeks getallen toe aan elk klein kwadrant. Als we de reeks bijvoorbeeld beginnen met 1, zijn de reeksen: 1-9 (eerste), 10-18 (vierde), 19-27 (tweede) en 28-36 (derde).
Conway’s LUX-methode voor magische vierkanten
We zullen dit laatste systeem gebruiken als we magische vierkanten van de orde 4n + 2 willen genereren, waarbij n een natuurlijk getal is. De procedure die we zullen volgen om vierkanten van deze stijl te maken is dus als volgt:
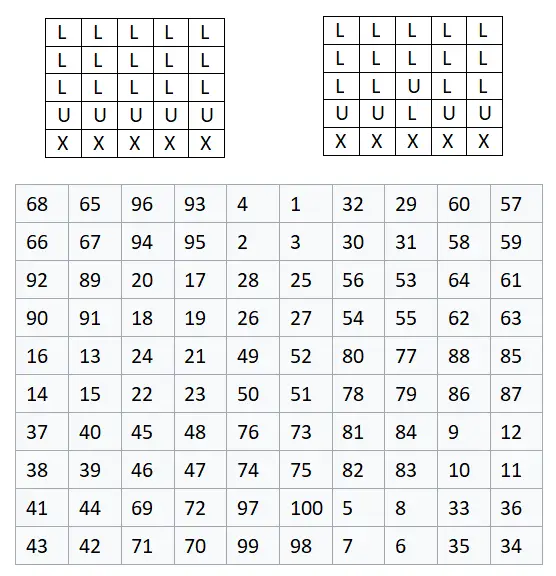
- Het maken van de tabel of matrix: we beginnen met het maken van een matrix van graad 2n + 1, waarbij n een natuurlijk getal is. Hiermee kunnen we de tafel ontwerpen en de mate ervan in gedachten houden en dan beginnen met het ontwerp.
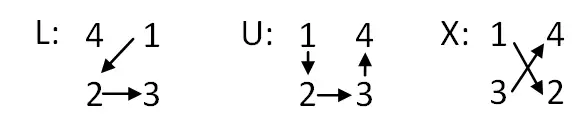
- Positionering van de letters: zodra de tabel is opgebouwd, moet je van boven naar beneden schrijven: n + 1 regel L, 1 regel U en n – 1 regel X. En dan moet je de U verwisselen in het midden met de L bovenaan.
- Wissel letters om voor numerieke waarden: Nu moeten we de letters vervangen door groepen van vier opeenvolgende cijfers. Afhankelijk van de letter geven we een of andere volgorde aan de cijfers. Hieronder uitgelegd:
We beginnen met het construeren van een matrix van 5×5 , dus n = 2, aangezien: 2n + 1 = 2 · 2 + 1 = 5. Dit betekent dat de matrix uiteindelijk een grootte zal hebben van 10×10, want als we we hebben al gezegd dat elke cel die een letter bevat gelijk is aan een groep van vier cijfers, dat wil zeggen een 2×2 matrix. Hieronder ziet u het voltooide voorbeeld, waarin we elke letter hebben vervangen door een groep van vier cijfers in de volgorde die in de afbeelding wordt weergegeven:
magische vierkanten oefeningen
Vervolgens bieden we je een aantal onvolledige magische vierkanten aan en je zult ze zelf moeten invullen, dankzij de concepten die we in dit artikel hebben uitgelegd. Vergeet niet dat u alle aangeleerde methoden kunt gebruiken. Bovendien moet u er rekening mee houden dat 1 mogelijk niet het eerste getal in de reeks is, hoewel dit wel in de aangifte wordt vermeld. En als je een van de oefeningen hebt afgerond, kun je de oplossing onder de stelling zien.
3×3 magisch vierkant
Construeer een magisch vierkant van 3×3 met alleen oneven getallen:
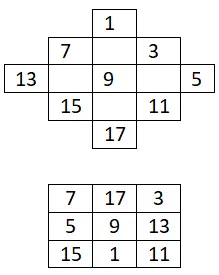
4×4 magisch vierkant
Voltooi het volgende 4×4 magische vierkant:
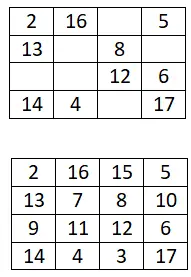
5×5 magisch vierkant
Voltooi het volgende magische vierkant van 5×5:
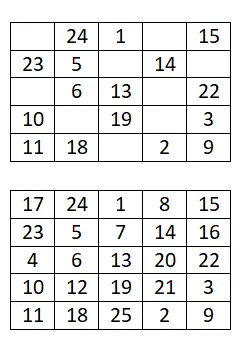
6×6 magisch vierkant
Voltooi het volgende magische vierkant van 6×6: