Lineaire regressie is een statistische methode die wordt gebruikt om de relatie tussen twee continue variabelen te bestuderen . Het belangrijkste idee van lineaire regressie is het vinden van de rechte lijn die het beste bij de gegevens past. Bovendien kunt u hiermee de waarde van de ene variabele voorspellen op basis van de waarde van een andere.
Deze rechte lijn heet ‘regressie’ en wordt gebruikt om onbekende waarden te voorspellen of om de relatie tussen variabelen te begrijpen. Samenvattend is lineaire regressie een hulpmiddel voor het analyseren en modelleren van de relatie tussen twee continue variabelen.
Waarom is lineaire regressie belangrijk?
Lineaire regressie is belangrijk omdat je hiermee de relatie tussen twee continue variabelen kunt modelleren en analyseren , wat handig kan zijn voor het voorspellen van toekomstige waarden en het identificeren van patronen en trends in gegevens.
Bovendien is lineaire regressie een fundamenteel hulpmiddel in de statistiek en de meeste gebieden van wetenschappelijk en sociaal onderzoek, waaronder onder meer economie, psychologie, geneeskunde, techniek en natuurkunde. Het wordt ook gebruikt bij zakelijke besluitvorming en procesoptimalisatie in de industrie en het bedrijfsleven.
Samenvattend is lineaire regressie een krachtig en veelzijdig hulpmiddel dat analyse en een beter begrip van gegevens en relaties tussen variabelen in verschillende onderzoeks- en praktijkgebieden mogelijk maakt .
Wat zijn de soorten lineaire regressie?
Er zijn verschillende soorten lineaire regressie, waarvan sommige:
eenvoudige lineaire regressie
Eenvoudige lineaire regressieanalyse is een veelgebruikt hulpmiddel om het effect van een onafhankelijke variabele op een enkele afhankelijke variabele te bestuderen , waarbij wordt aangenomen dat er een lineair verband tussen beide bestaat. Met de eenvoudige lineaire regressievergelijking kunnen we de waarden van de afhankelijke variabele schatten op basis van de waarden van de onafhankelijke variabele.
De eenvoudige lineaire regressieformule is:
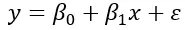
Waarbij β 0 de waarde is van de afhankelijke variabele wanneer de onafhankelijke variabele nul is. β 1 vertegenwoordigt de verandering in de afhankelijke variabele per eenheidsverandering in de onafhankelijke variabele en ε vertegenwoordigt het residu of de fout. Dat wil zeggen, de variabiliteit van de gegevens die niet kan worden verklaard door de lineaire relatie van de formule.
Meerdere lineaire regressie
Meervoudige lineaire regressie wordt gebruikt als er meer dan één onafhankelijke variabele is die de afhankelijke variabele die wordt bestudeerd, kan beïnvloeden .
De formule voor meervoudige lineaire regressie is:
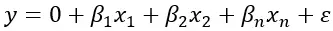
Waar Y de afhankelijke variabele vertegenwoordigt , zijn β 1 , β 2 , β n de onafhankelijke variabelen die de waarde van Y kunnen beïnvloeden, regressie en ε vertegenwoordigt de mogelijk bestaande fout. Met deze formule kunnen we de waarde van Y schatten op basis van de waarden van de onafhankelijke variabelen.
Wat is de lineaire regressieformule?
De lineaire regressieformule is:
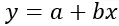
Goud:
y is de afhankelijke variabele (of respons) die moet worden voorspeld
x is de onafhankelijke (of voorspellende) variabele die wordt gebruikt om de voorspelling te doen
a is het snijpunt (of het punt waar de regressielijn de Y-as snijdt wanneer x=0)
b is de helling van de regressielijn (die de mate van verandering van y aangeeft voor elke verandering van x)
Om de waarden van a en b te vinden, gebruiken we de kleinste kwadratenmethode die de som van de kwadratische fouten tussen de waargenomen waarden en de waarden voorspeld door de regressielijn probeert te minimaliseren.
Hier zijn de formules:
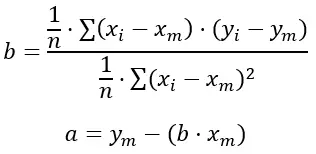
Goud:
n is het totale aantal datasets dat we hebben.
x i en y i zijn de waarden die we nemen in de sommatie.
x m en y m zijn de gemiddelde waarden van elke variabele.
Hoe de lineaire regressiemethode toepassen?
De lineaire regressiemethode kan worden toegepast door de onderstaande stappen te volgen:
- Gegevens verzamelen : Het eerste dat u moet doen, is de gegevens verzamelen die u interesseren. Als u bijvoorbeeld de relatie tussen het salaris en de leeftijd van een groep mensen wilt bestuderen, moet u informatie verzamelen over het salaris en de leeftijd van elk van hen.
- De gegevens plotten – Vervolgens moet u de gegevens op een cartesiaans vlak plotten, waarbij de onafhankelijke variabele (in dit geval leeftijd) op de horizontale as wordt geplaatst en de afhankelijke variabele (salaris) op de verticale as.
- Bepaal de regressielijn : De regressielijn die het beste bij de gegevens past, moet worden bepaald. Deze lijn wordt verkregen uit de lineaire regressieformule, die wordt berekend met behulp van de statistische voorbeeldgegevens .
- Beoordeel Goodness of Fit – Het is belangrijk om te beoordelen hoe goed de regressielijn bij de gegevens past. Dit kan gedaan worden met behulp van statistische metingen.
- Voorspellingen doen – Ten slotte kunnen voorspellingen worden gedaan met behulp van de resulterende regressielijn. Als u bijvoorbeeld het salaris van een 30-jarige wilt voorspellen, gebruikt u de lineaire regressieformule en vult u de waarde van de leeftijd daarin in.
Het is belangrijk op te merken dat deze stappen enigszins kunnen variëren, afhankelijk van het gebruikte type lineaire regressie en de gebruikte statistische software.
Waar wordt lineaire regressie voor gebruikt?
Lineaire regressie wordt gebruikt wanneer u de relatie tussen twee variabelen wilt analyseren , waarbij één variabele de waarde van een andere variabele kan beïnvloeden. Daarom kan lineaire regressie worden gebruikt om te begrijpen hoe een onafhankelijke variabele een afhankelijke variabele beïnvloedt en om de waarde van de afhankelijke variabele te voorspellen op basis van de onafhankelijke variabele.
Het is belangrijk op te merken dat lineaire regressie ervan uitgaat dat de relatie tussen de twee variabelen lineair is , wat betekent dat de verandering in de afhankelijke variabele evenredig is aan de verandering in de onafhankelijke variabele.
Daarom moet lineaire regressie worden gebruikt wanneer een lineair verband tussen de twee variabelen wordt vermoed. Als niet aan deze voorwaarde wordt voldaan, kan het passender zijn om andere niet-lineaire regressiemodellen of andere statistische methoden te gebruiken.
Wat zijn de toepassingen van lineaire regressie?
Lineaire regressie wordt gebruikt in een breed scala aan toepassingen op gebieden als onder meer statistiek, economie, techniek, sociale wetenschappen en biologie. Hier zijn enkele van de meest voorkomende toepassingen van lineaire regressie:
- Trendanalyse – Om trends in historische gegevens te analyseren en toekomstige trends te voorspellen.
- Forecasting – Het voorspellen van de toekomstige waarde van een variabele op basis van eerdere waarden van een of meer variabelen.
- Marktonderzoek : studie van de relatie tussen de vraag naar een product en de prijs ervan.
- Financiële analyse – Het bestuderen van de relatie tussen de inkomsten en uitgaven van een bedrijf en het voorspellen van toekomstige financiële resultaten.
- Epidemiologische studies : onderzoek naar de relatie tussen blootstelling aan een risicofactor en de kans op het ontwikkelen van een ziekte.
- Sociale wetenschappen – Het bestuderen van de relatie tussen twee of meer variabelen op gebieden als psychologie, sociologie en politieke wetenschappen.
- Operations Research – Lineaire regressie wordt gebruikt om complexe systemen op gebieden als industriële techniek en logistiek te modelleren en optimaliseren.
- Milieuwetenschappen – Wordt gebruikt om de relatie tussen omgevingsfactoren en effecten op ecosystemen te bestuderen.
Wat zijn residuen bij lineaire regressie?
De residuen bij lineaire regressie zijn het verschil tussen de waargenomen waarden van de afhankelijke variabele en de waarden voorspeld door het lineaire regressiemodel . Met andere woorden, het is de verticale afstand tussen de feitelijke gegevenspunten en de regressielijn.
Het idee achter residuen is dat als de regressielijn goed bij de gegevens past, de residuen klein en willekeurig moeten zijn. Als de residuen groot zijn of een bepaald patroon volgen, kan dit een teken zijn dat de relatie tussen de variabelen niet lineair is of dat het lineaire regressiemodel niet past bij de gegevens.
Residuen worden ook gebruikt om de nauwkeurigheid van het lineaire regressiemodel te evalueren en om uitschieters of invloedrijke gegevenspunten te identificeren die de kwaliteit van het model kunnen beïnvloeden.
Kan ik lineaire regressie uitvoeren met meer dan één afhankelijke variabele?
Bij lineaire regressie is de afhankelijke variabele altijd een enkele variabele. U kunt echter meer dan één onafhankelijke variabele hebben. In dit geval zouden we spreken van meervoudige lineaire regressie .
Bij meervoudige lineaire regressie is het doel om het effect van meerdere onafhankelijke variabelen op een enkele afhankelijke variabele te bestuderen.
Hoe kan ik coëfficiënten interpreteren in lineaire regressie?
Bij lineaire regressie vertegenwoordigen de coëfficiënten de helling en het snijpunt van de regressielijn . De helling geeft de verandering in de afhankelijke variabele aan per eenheid verandering in de onafhankelijke variabele, terwijl het snijpunt de waarde van de afhankelijke variabele vertegenwoordigt wanneer de onafhankelijke variabele gelijk is aan nul.
Numerieke voorbeelden van lineaire regressie
Een eenvoudig voorbeeld zou het volgende kunnen zijn:
Stel dat we voor een groep mensen de volgende leeftijds- en lengtegegevens hebben:
| leeftijd) | Hoogte (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Vier vijf | 190 |
Wij willen nagaan of er een verband bestaat tussen de leeftijd en lengte van deze mensen. Om dit te doen, zullen we lineaire regressie gebruiken.
Eerst kunnen we een statistische grafiek tekenen met de gegevens (in dit geval raden we aan een spreidingsdiagram te gebruiken):
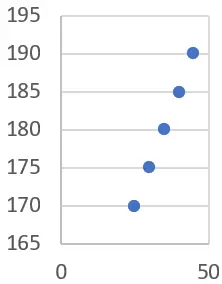
We kunnen zien dat er een duidelijke trend is dat naarmate de leeftijd toeneemt, de lengte ook toeneemt. We kunnen dit bevestigen door de lineaire regressielijn te berekenen.
Door de coëfficiënten van de lineaire regressielijn te berekenen met de formules die we eerder zagen, verkrijgen we:
bij = 145
b = 1
Daarom is de vergelijking van de lineaire regressielijn:
Lengte = 145 + 1 Leeftijd
We kunnen deze vergelijking gebruiken om de lengte van een persoon te voorspellen op basis van zijn leeftijd. Als een persoon bijvoorbeeld 32 jaar oud is, kunnen we voorspellen dat zijn lengte:
Hoogte = 145 + 1 32 = 177 cm