Op deze pagina vindt u de uitleg van wat een lineaire combinatie tussen vectoren betekent. Daarnaast krijg je een voorbeeld te zien van hoe een vector wordt uitgedrukt als een lineaire combinatie en daarnaast kun je oefenen met oefeningen en stap voor stap opgeloste problemen.
Wat is een lineaire combinatie van vectoren?
De definitie van lineaire combinatie is als volgt:
Een lineaire combinatie van een set vectoren is de vector die wordt verkregen door alle vectoren in de set op te tellen, vermenigvuldigd met scalaire getallen (reële getallen).
Met andere woorden, gegeven een reeks vectoren
![]()
een lineaire combinatie hiervan zou zijn:
![]()
Waar de coëfficiënten
![]()
Dit zijn echte cijfers.
Daarom betekent een vector die een lineaire combinatie is van andere vectoren dat de eerste kan worden uitgedrukt in termen van de tweede.
Dit concept kan beter worden begrepen door een vector in het vlak weer te geven, wat een lineaire combinatie is van twee vectoren:
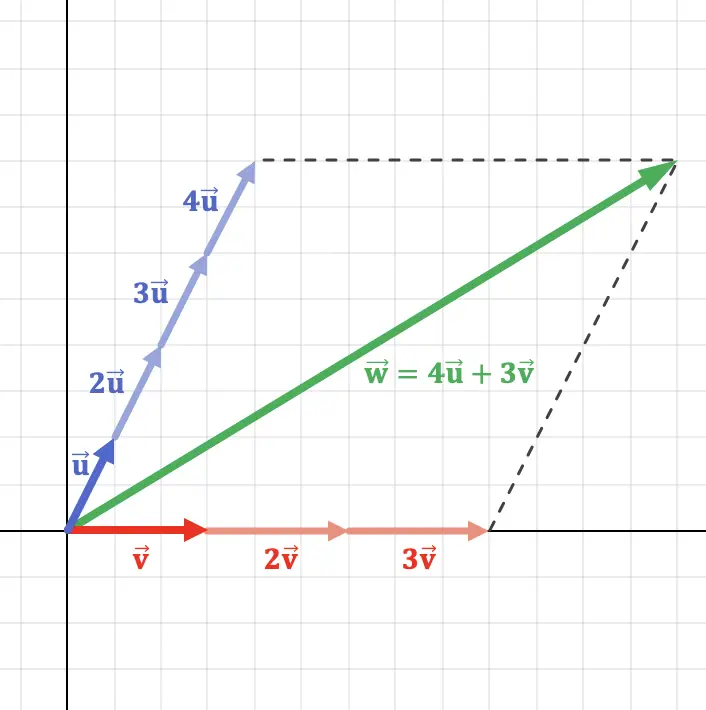
Zoals je kunt zien in de grafische weergave hierboven, is de vector
![]()
kan worden verkregen uit vectoren
![]()
En
![]()
vectorbewerkingen uitvoeren. Daarom de vector
![]()
is een lineaire combinatie van de andere twee vectoren.
Benadrukt moet worden dat deze lineaire combinatie uniek is, of met andere woorden, er is slechts één haalbare lineaire combinatie voor elke vector. Omdat we, volgens het vorige voorbeeld, vermenigvuldigden
![]()
voor 6 in plaats van 4 zouden we een andere vector verkrijgen.
Bovendien is een van de eigenschappen van de lineaire combinatie in het vlak (in R2) dat elke vector kan worden voorgesteld als een lineaire combinatie van twee andere vectoren als ze verschillende richtingen hebben, dat wil zeggen als ze niet evenwijdig zijn.
Soms kunnen we ook met het oog vaststellen dat twee vectoren een lineaire combinatie zijn. Om dit te doen, is het voldoende dat de componenten proportioneel zijn. De coördinaten van de volgende twee vectoren zijn bijvoorbeeld proportioneel en daarom zijn de vectoren een lineaire combinatie:
![]()
![Rendered by QuickLaTeX.com \cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac41542948764e158ebe590c6b36e67_l3.png)
Tenslotte, of het nu in een tweedimensionale (in R2) of driedimensionale (in R3) vectorruimte is, als er een lineaire combinatie is binnen een reeks vectoren, impliceert dit dat ze lineair van elkaar afhankelijk zijn. Aan de andere kant, als er geen lineaire combinatie mogelijk is tussen de vectoren, betekent dit dat ze lineair onafhankelijk zijn.
Als dit laatste concept u niet helemaal duidelijk is, raden we u aan onze uitleg van lineair afhankelijke en onafhankelijke vectoren te bekijken. Hier vindt u wat het betekent voor vectoren om lineair afhankelijk of onafhankelijk te zijn, voorbeelden van elk type en de verschillen daartussen. . Dit concept wordt veel gebruikt en wordt zelfs veel gevraagd op examens, dus het is belangrijk dat je het goed begrijpt.
Hoe je een vector uitdrukt als een lineaire combinatie van andere vectoren
Vervolgens zullen we zien hoe we een typisch probleem kunnen oplossen waarbij ons wordt gevraagd de lineaire combinatie van een vector te vinden.
- Druk de vector uit
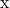
als een lineaire combinatie van
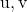
En
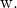
![]()
![]()
Dus de vector
![]()
een lineaire combinatie is van de andere vectoren, moet aan de volgende vergelijking worden voldaan:
![]()
Waar de coëfficiënten
![]()
En
![]()
Dit zijn de onbekenden die we moeten vinden.
We vervangen daarom elke vector door zijn coördinaten:
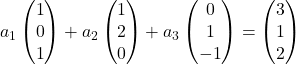
We vermenigvuldigen elke vector met zijn coëfficiënt:
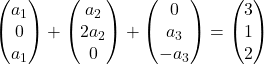
We voegen vectoren toe:
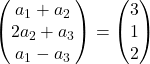
Elke linkercoördinaat moet gelijk zijn aan elke rechtercoördinaat. We hebben daarom 3 vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e5fe050102a285a325dcd81d07ef5d5_l3.png)
Het enige dat overblijft is het oplossen van het verkregen stelsel van vergelijkingen. Gebruik hiervoor de methode van uw voorkeur (substitutiemethode, de regel van Cramer, Gauss-Jordan-methode, enz.), In dit geval gebruiken we de Gauss-methode:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8aa4e245614f286e0697797a18ba4465_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f1d9c941fe239bb40297b998eb6929_l3.png)
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-02a8a00406479f367627b682099e05c0_l3.png)
Het verkregen stappensysteem is daarom:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74ed1b18779582d6683ecaa1a9085e3d_l3.png)
Het enige wat we nu moeten doen is de onbekende factoren ophelderen en de waarde ervan ontdekken. Dus uit de laatste vergelijking die we vinden
![]()
![]()
Uit de tweede vergelijking van het systeem berekenen we de waarde van
![]()
![]()
![]()
![]()
![]()
En ten slotte vinden we uit de eerste vergelijking van het stappensysteem het onbekende
![]()
![]()
De oplossing voor het stelsel lineaire vergelijkingen is daarom:
![]()
De vector dus
![]()
Het kan worden uitgedrukt door de volgende lineaire combinatie:
![]()
![]()
![]()
Er is dus feitelijk een lineaire afhankelijkheid tussen de vectoren. Aan de andere kant, als er geen oplossing voor het stelsel vergelijkingen was verkregen, zou dit betekenen dat de vector
![]()
Het is lineair onafhankelijk ten opzichte van de andere vectoren en daarom zou er geen mogelijke lineaire combinatie zijn om de genoemde vector uit de andere vectoren te verkrijgen.
Opgeloste oefeningen over de lineaire combinatie van vectoren
Oefening 1
Geef van de volgende drie vectoren aan welke paren lineaire combinaties van elkaar zijn. Zoek bovendien de lineaire combinatierelatie van genoemde vectorparen.
![]()
Om te weten of een paar vectoren een lineaire combinatie is, moeten we kijken of hun coördinaten proportioneel zijn.
We controleren eerst de vector
![]()
met de vector
![]()
![]()
Ten tweede controleren we de vector
![]()
met de vector
![]()
![]()
Ten slotte testen we de vector
![]()
met de vector
![]()
![Rendered by QuickLaTeX.com \cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f818eb5ae0825dd43290331519599c21_l3.png)
Het enige paar vectoren dat lineaire combinaties is, is dus:
![]()
En
![]()
Bovendien is hun relatie als volgt:
![]()
Of gelijkwaardig:
![]()
Hoewel de verklaring dit niet vereist, zijn de enige vectoren die lineair van elkaar afhankelijk zijn dat wel
![]()
En
![]()
omdat er een lineaire combinatie tussen beide bestaat. De andere paren zijn lineair onafhankelijk, omdat ze niet lineair kunnen worden gecombineerd.
Oefening 2
Zoek de lineaire relatie tussen de vector
![]()
en de set vectoren
![]()
En
![]()
![]()
![]()
Dus de vector
![]()
een lineaire combinatie is van de andere vectoren, moet aan de volgende vergelijking worden voldaan:
![]()
We vervangen daarom elke vector door zijn coördinaten:
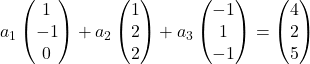
We vermenigvuldigen elke vector met zijn constante:
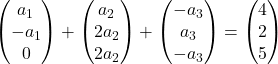
We voegen de vectoren toe:
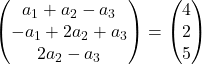
We verkrijgen daarom het volgende stelsel vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ea3ca998fc7d9d9b2cf42d43a5bf0a4_l3.png)
We lossen het systeem op dat is verkregen met de Gauss-methode:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c808441bc71bd26e333ebe2169b738ca_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-941792a2de155bc284b14e34dc561418_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7105de2fa579f40818bccc2df48961ab_l3.png)
Het verkregen stappensysteem is daarom:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd5b2d564f66cd225c1a5987241ba14_l3.png)
Het enige wat we nu moeten doen is de onbekende factoren ophelderen en de waarde ervan ontdekken. Dus uit de laatste vergelijking die we vinden
![]()
![]()
![]()
Uit de tweede vergelijking van het systeem berekenen we de waarde van
![]()
![]()
![]()
En ten slotte vinden we uit de eerste vergelijking van het stappensysteem het onbekende
![]()
![]()
![]()
![]()
De oplossing voor het stelsel lineaire vergelijkingen is daarom:
![]()
De vector dus
![]()
Het kan worden uitgedrukt door de volgende lineaire combinatie:
![]()
![]()
![]()
Oefening 3
Druk de vector uit
![]()
als een lineaire combinatie van vectoren
![]()
En
![]()
![]()
![]()
We stellen de lineaire combinatievergelijking voor met betrekking tot de vector
![]()
![]()
We vervangen daarom elke vector door zijn componenten:
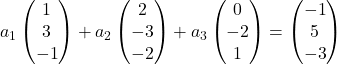
We vermenigvuldigen elke vector met zijn respectievelijke onbekende:
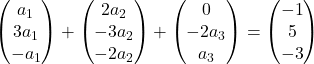
We voeren de toevoeging van vectoren uit:
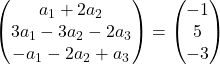
We hebben daarom het volgende stelsel vergelijkingen verkregen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acdcf13a945bca16684be340d27e3523_l3.png)
We lossen het systeem op dat is verkregen met de Gauss-methode:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e49ae26fc68a865214bd9b6146b7aa99_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4c56b420242d0abe6f77b3ed1a60e54_l3.png)
Het verkregen stappensysteem is daarom:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-03461ed9ebda463d2f0a1bb6894657be_l3.png)
Het enige wat we nu moeten doen is de onbekende factoren ophelderen en de waarde ervan ontdekken. Dus uit de laatste vergelijking die we vinden
![]()
![]()
Uit de tweede vergelijking van het systeem vinden we de waarde van
![]()
![]()
![]()
![]()
![]()
![]()
En ten slotte lossen we vanaf de eerste vergelijking van het stappensysteem het onbekende op
![]()
![]()
De oplossing voor het stelsel lineaire vergelijkingen is daarom:
![]()
De vector dus
![]()
kan worden uitgedrukt door de andere vectoren lineair te combineren:
![]()
![]()
![]()
Oefening 4
Bepaal of de vector
![]()
kan worden uitgedrukt als een lineaire combinatie van de vectoren
![]()
En
![]()
Zoek in dit geval de uitdrukking die ze verbindt.
![]()
![]()
Dus de vector
![]()
een lineaire combinatie is van de andere vectoren, moet aan de volgende vergelijking worden voldaan:
![]()
We vervangen daarom elke vector door zijn coördinaten:
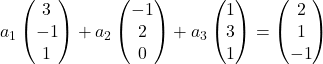
We vermenigvuldigen elke vector met zijn coëfficiënt:
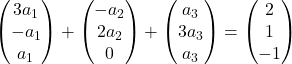
We voegen de vectoren toe:
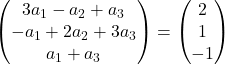
De voorgaande uitdrukking is daarom equivalent aan het volgende stelsel vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f51b7e801b8314c51b983f1f24be15e4_l3.png)
We lossen nu het systeem op dat is verkregen met de Gauss-methode:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-031b14d5aca6a41d897ca575440b1197_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2caf1e1104b8b67e13d452bbd20d13b0_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4deec2426c0b9bb0b8e8a3d95155fd9_l3.png)
We hebben daarom het volgende stelsel vergelijkingen verkregen:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e537d5c481ceedeaebf95334d72199ad_l3.png)
Aan de laatste vergelijking kan echter nooit worden voldaan, aangezien 0 nooit gelijk zal zijn aan -30, ongeacht de waarden die de onbekenden aannemen. Daarom heeft het systeem geen oplossing en dit impliceert dat er geen lineaire combinatie is om de vector te berekenen
![]()