In dit artikel leggen we uit hoe je de boogsinus van een functie kunt afleiden. Je vindt er voorbeelden van afgeleiden van de boogsinus van functies en je kunt zelfs oefenen met oefeningen die stap voor stap worden opgelost. Ten slotte zul je ook de demonstratie zien van de arcsine-afgeleide formule.
Wat is de afgeleide van de boogsinus?
De boogsinusafgeleide van x is één gedeeld door de vierkantswortel van één minus x kwadraat.
![]()
Daarom is de afgeleide van de boogsinus van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door de vierkantswortel van één minus de kwadratische functie.
![]()
Logischerwijs wordt de tweede formule verkregen door de kettingregel op de eerste formule toe te passen.
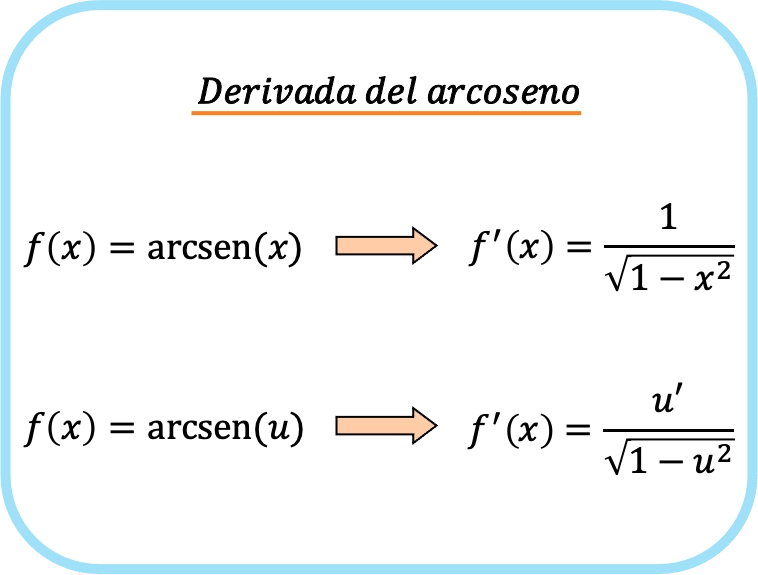
Onthoud dat boogsinus de inverse functie van sinus is, en daarom wordt het ook wel inverse sinus genoemd.
Voorbeelden van arcsinusderivaat
Nadat we hebben gezien wat de formule voor de boogsinusderivaat is, zullen we verschillende voorbeelden van dit soort trigonometrische derivaten uitleggen. Op deze manier wordt het gemakkelijker voor u om te begrijpen hoe de boogsinus van een functie wordt afgeleid.
Voorbeeld 1: Afgeleide van de boogsinus van 2x
![]()
Om de afgeleide van de boogsinusfunctie te vinden, moeten we de overeenkomstige formule gebruiken:
![]()
Dus de afgeleide van 2x is 2, dus de boogsinusafgeleide van 2x is 2 gedeeld door de wortel van één minus 2x kwadraat:
![]()
Voorbeeld 2: Afgeleide van de boogsinus van x kwadraat
![]()
We gebruiken de arcsine-afgeleide formule om deze af te leiden:
![]()
De functie x 2 is van de tweede graad, dus de afgeleide ervan is 2x. De afgeleide van de boogsinus van x verheven tot de macht 2 is dus:
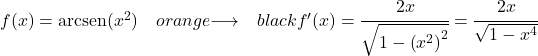
Voorbeeld 3: Afgeleide van de boogsinus van e x
![]()
De functie in dit voorbeeld is een samengestelde functie, dus we moeten de kettingregel toepassen om de afgeleide op te lossen:
![]()
De afgeleide van e x is zichzelf, dus de afgeleide van de gehele functie is:
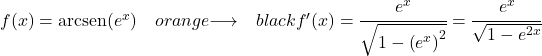
Arcsine-afgeleide opgeloste problemen
Leid de volgende boogsinusfuncties af:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
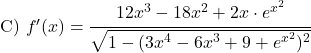
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
Bewijs van de arcsine-afgeleide formule
Vervolgens gaan we verder met het wiskundige bewijs van de formule voor de afgeleide van de boogsinus.
![]()
Eerst transformeren we de boogsinus in sinus:
![]()
Nu differentiëren we beide kanten van de vergelijking:
![]()
Wij zuiveren u:
![]()
Vervolgens passen we de fundamentele trigonometrische identiteit toe:
![]()
![]()
En zoals we hierboven hebben afgeleid dat x equivalent was aan de sinus van y, blijft de gelijkheid bestaan:
![]()
Zoals je kunt zien, hebben we door deze procedure toe te passen de formule verkregen voor de afgeleide van de boogsinusfunctie, dus er wordt aangetoond dat aan de formule is voldaan.