Een kwadratische vergelijking of kwadratische vergelijking is een vergelijking van graad 2, waarbij de grootste exponent van een van de termen gelijk is aan 2. Dit betekent dat de vergelijking maximaal twee verschillende oplossingen kan hebben, hoewel deze ook een unieke oplossing of helemaal niet.
Om de oplossingen of wortels van kwadratische vergelijkingen te berekenen, kunnen we twee verschillende procedures volgen: door middel van de kwadratische formule of door de uitdrukking in factoren te ontbinden . In dit artikel bespreken we beide methoden en geven we je enkele praktische oefeningen. Voordat we echter enkele concepten gaan verduidelijken, zodat de hele uitleg heel goed wordt begrepen en je het meeste uit het lezen haalt.
Soorten kwadratische vergelijkingen
De belangrijkste indeling tussen kwadratische vergelijkingen is gebaseerd op de structuur van de uitdrukking zelf. De standaard- of gebruikelijke structuur van deze uitdrukkingen is dus als volgt: ax² + bx + c . Deze veel voorkomende vorm is equivalent aan een volledige vergelijking, maar als er nul- of nultermen zijn, kan de structuur variëren, en dat is waar onvolledige vergelijkingen verschijnen. Vervolgens zullen we de kenmerken van alle typen nader toelichten.
Volledige kwadratische vergelijkingen
Zoals we al zeiden, hebben we de volledige kwadratische vergelijkingen , deze hebben alle coëfficiënten a, b en c niet nul. De uitdrukking volgt daarom de structuur ax² + bx + c tot op de letter, aangezien deze alle termen bevat: de kwadratische term, de lineaire term en de onafhankelijke term. Een voorbeeld van dit type is de volgende vergelijking: x² + 2x + 1 = 0.
Onvolledige kwadratische vergelijkingen
Wat onvolledige vergelijkingen betreft, we kunnen ze onderscheiden op basis van welke coëfficiënt gelijk is aan nul. Houd er rekening mee dat als deze uitleg uw twijfels niet oplost, hieronder een afbeelding staat waarin u alle gevallen stap voor stap kunt uitleggen.
- Onvolledige vergelijkingen (b = 0): in deze eerste situatie vinden we een uitdrukking die de volgende structuur volgt: ax² + c = 0. Hiermee verkrijgen we twee resultaten: de negatieve en de positieve van de wortel van de breuk c/a .
- Onvolledige vergelijkingen (c = 0): als we de vorm ax² + bx = 0 hebben, moeten we de vergelijking in factoren ontbinden om de uitdrukking x (ax + b) = 0 te krijgen. We zullen daarom twee oplossingen hebben: x = 0 en x = – z/a.
- Onvolledige vergelijkingen (b = c = 0): in dit geval hebben we een vergelijking ax² = 0 en hebben we maar één mogelijke oplossing, namelijk x = 0.
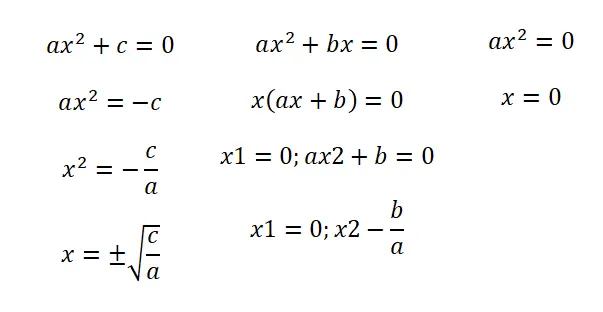
Het is de moeite waard te vermelden dat de procedures die we je hebben geleerd je in staat stellen sneller te gaan bij het oplossen van onvolledige vergelijkingen. Maar in alle gevallen kunt u de kwadratische formule gebruiken die we u hieronder zullen leren, u hoeft alleen maar een nul te schrijven in de coëfficiënten die niet bestaan.
Formule voor kwadratische vergelijkingen
Om kwadratische vergelijkingen (ax² + bx + c = 0) op te lossen, moeten we de algemene formule of kwadratische formule toepassen en vervolgens de numerieke waarden vervangen die overeenkomen met elke letter in de wiskundige uitdrukking.
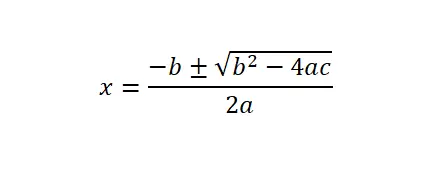
Het is ook belangrijk om uit te leggen dat de discriminant (Δ) de uitdrukking b² – 4ac is, die zich onder de vierkantswortel bevindt. Vanuit dit wiskundige concept kunnen we weten hoeveel oplossingen deze kwadratische vergelijking heeft. In principe zijn er drie opties: de discriminant is negatief (er zijn geen echte oplossingen), de discriminant is nul (er is maar één oplossing) of de discriminant is positief (er zijn twee oplossingen).
Voorbeeld van een volledige kwadratische vergelijking opgelost
Probeer de volgende kwadratische vergelijking op te lossen: 2x²+4x-6=0 en controleer je resultaat met de onderstaande vergelijking. We raden u aan de volgende procedure te volgen: analyseer het type vergelijking (identificeer de nultermen), bereken de discriminant om het aantal bestaande oplossingen te kennen en los ten slotte de voorgestelde vergelijking op met de formule.
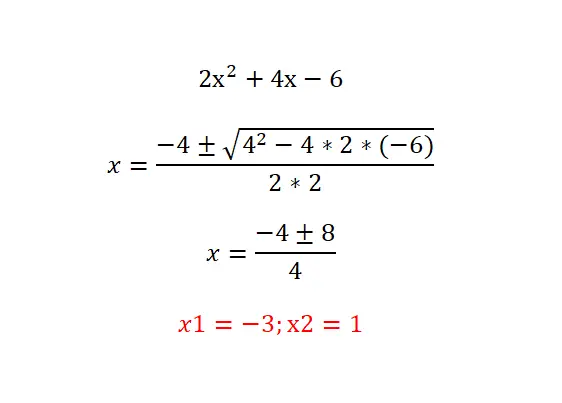
Factoriële kwadratische vergelijkingen
De tweede methode die we hebben voor het oplossen van kwadratische vergelijkingen is factorisatie . Om een polynoom (in ons geval een kwadratisch polynoom) in factoren te ontbinden , kunnen we dus verschillende methoden gebruiken. Hoewel vergelijkingen van deze stijl over het algemeen meestal factoreerbaar zijn met een gemeenschappelijke term. En zo niet, dan kunt u Notable Identities proberen toe te passen, maar normaal gesproken hoeft u in deze situaties geen andere methoden te kennen.
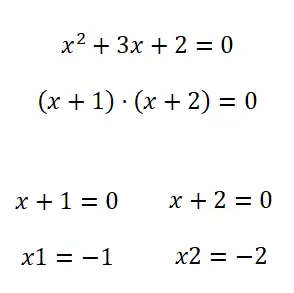
Kwadratische vergelijkingen oefeningen met oplossingen
Hieronder vind je een reeks oefeningen over volledige en onvolledige kwadratische vergelijkingen . Op deze manier bekijk je alle theorie die in dit artikel wordt uitgelegd en wordt het duidelijker voor je hoe je deze in de oefeningen kunt toepassen. We raden u aan om ze zelf op te lossen en pas naar de oplossing te kijken als u ze hebt voltooid of als u vastloopt. Dat gezegd hebbende, kun je nu beginnen met het oplossen van de oefeningen.
Oefening 1
Los de volgende kwadratische vergelijking op:
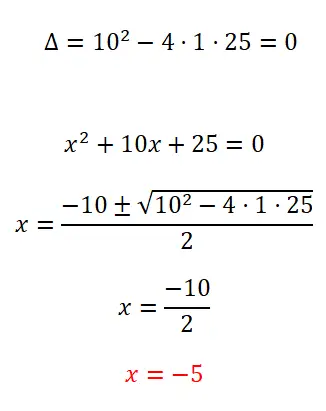
- We beginnen met het berekenen van de discriminant, om het aantal mogelijke oplossingen te kennen.
- Omdat dit een volledige kwadratische vergelijking is, passen we de kwadratische formule toe en lossen we de berekeningen op.
- We verkrijgen de waarde van de onbekende x.
Oefening 2
Los de volgende kwadratische vergelijking op:
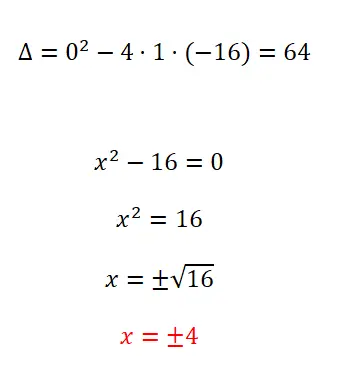
- We beginnen met het berekenen van de discriminant.
- Omdat we een onvolledige kwadratische vergelijking hebben waarin b = 0, passen we de standaard toe voor dit soort vergelijkingen.
- We lossen de berekening op om het resultaat te krijgen, en we mogen het teken ± niet vergeten.
Oefening 3
Los de volgende ongeordende kwadratische vergelijking op:
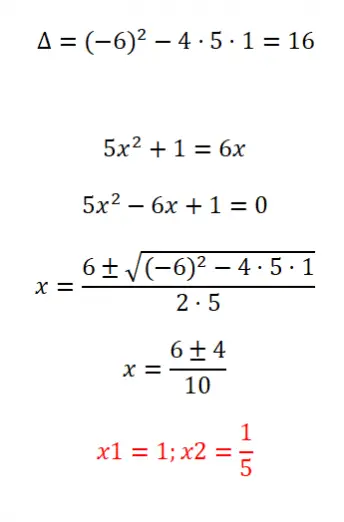
- We beginnen met het berekenen van de discriminant van de vergelijking.
- Voordat we de formule kunnen toepassen, moeten we de vergelijking ordenen volgens de structuur ax² + bx + c = 0.
- Vervolgens passen we de algemene formule toe.
- En eindelijk krijgen we de resultaten.
Oefening 4
Los de volgende kwadratische vergelijking op door te ontbinden in factoren:
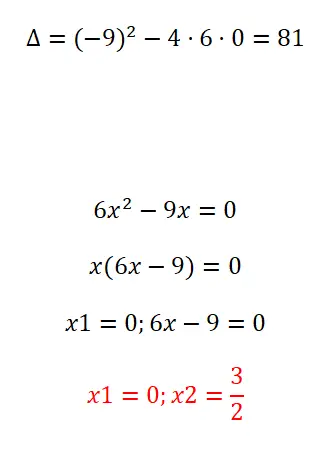
- We berekenen eerst de discriminant.
- Vervolgens extraheren we de gemeenschappelijke factor van x.
- De eerste oplossing is dus x = 0.
- En de tweede is x = 3/2.
Oefening 5
Los de volledige kwadratische vergelijking op die we hieronder laten zien:
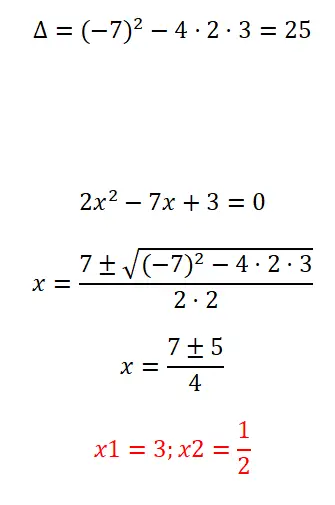
- Zoals altijd berekenen we de discriminant om erachter te komen hoeveel oplossingen de vergelijking in kwestie heeft.
- Vervolgens passen we de kwadratische formule toe, omdat het een volledige vergelijking is.
- Ten slotte drukken we het resultaat van de vergelijking uit.
Oefening 6
Los de kwadratische vergelijking op met breuken die wij aanbieden:
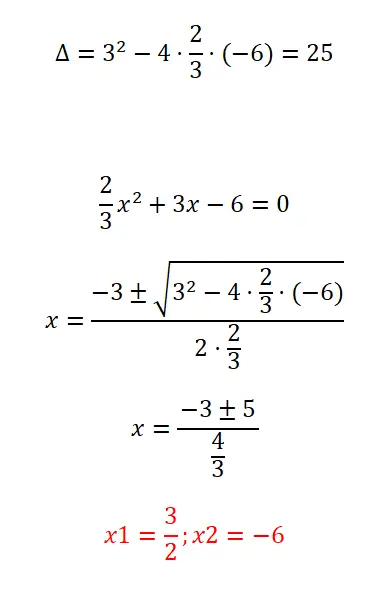
- We beginnen met het berekenen van de discriminant van de uitdrukking.
- Vervolgens passen we de kwadratische formule toe, waarbij we er rekening mee houden dat de coëfficiënt “a” wordt gevormd door een breuk.
- Wij lossen de berekening op.
- En we hebben al de twee wortels van de vergelijking.
Oefening 7
Los de volgende kwadratische vergelijking op:
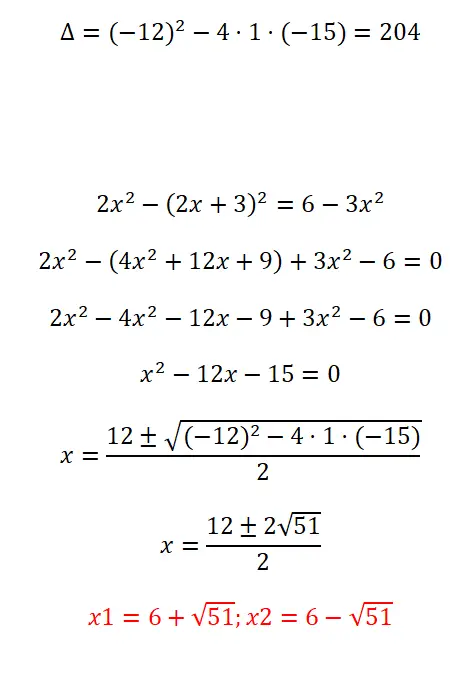
- We beginnen met het berekenen van de discriminant.
- Voordat we de formule toepassen, moeten we de uitdrukking vereenvoudigen en deze de vorm geven ax² + b + c = 0.
- We vervangen alle coëfficiënten in de formule en lossen de berekening op.
- Eindelijk krijgen we het resultaat.
Oefening 8
Bewijs van het oplossen van de volgende kwadratische vergelijking:
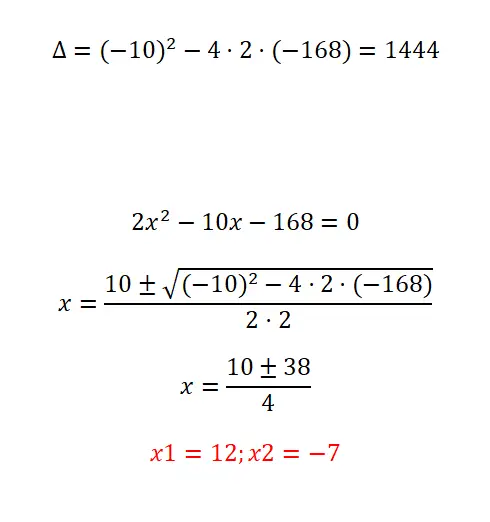
- We beginnen met het berekenen van de discriminant.
- Zoals je kunt zien, is dit een eenvoudige kwadratische vergelijking, hoewel deze vrij grote coëfficiënten heeft. Daarom moeten we de formule toepassen en voorzichtig zijn bij het uitvoeren van de bewerkingen.
- Uiteindelijk krijgen we beide mogelijke oplossingen.