Kwadratische functie of parabool

Op deze pagina wordt uitgelegd wat een kwadratische functie is, evenals al zijn kenmerken: kromming, hoekpunt, snijpunten met de assen, enz. Ook leer je hoe je een kwadratische functie in een grafiek kunt weergeven. En tot slot kun je oefenen met voorbeelden, stapsgewijze oefeningen en problemen op kwadratische functies.

Wat is een kwadratische functie?

De definitie van een kwadratische functie is als volgt:

In de wiskunde is een kwadratische (of parabolische) functie een polynomiale functie van graad 2, dat wil zeggen een functie waarin de term van de hoogste graad van de tweede graad is. Daarom is de formule voor een kwadratische functie:

f(x)=ax^2+bx+c

Goud:

  • ax^2

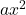
    is de kwadratische term.

  • bx

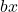
    is de lineaire term.

  • c

    is de onafhankelijke term.

Het domein van een kwadratische functie bestaat altijd uit reële getallen.

\text{Dom } f=\mathbff{R}

Concaviteit en convexiteit van een kwadratische functie

Het analyseren van de kromming van een kwadratische of parabolische functie is heel eenvoudig, omdat deze alleen afhangt van de kwadratische coëfficiënt.

  • Als de coëfficiënt

    a

    positief is, is de kwadratische functie convex (in de vorm

    \bm{\cup}

    ). De top is dus een minimum.

  • Als de coëfficiënt

    a

    negatief is, is de kwadratische functie concaaf (in de vorm van

    \bm{\cap}

    ). De piek is dus een maximum.

kwadratische functie of convexe parabool
kwadratische functie of concave parabool

Opmerking: de wiskundige gemeenschap is het er nog steeds niet helemaal mee eens en daarom zeggen sommige professoren het tegenovergestelde: ze noemen een functie concaaf en heeft de vorm van een

\bm{\cup}

, en een convexe functie die de vorm heeft van

\bm{\cap}

. Het gaat er in ieder geval om welke vorm de functie heeft, wat de naam ook is.


Hoekpunt van een kwadratische functie

Om een kwadratische functie te kunnen tekenen, is het noodzakelijk om de coördinaten van het hoekpunt van de parabool te kennen.

Om het hoekpunt van een kwadratische functie te vinden, moeten we de X-coördinaat van het punt berekenen met behulp van de volgende formule:

\displaystyle x=\frac{-b}{2a}

Vervolgens kunnen we de andere hoekpuntcoördinaat vinden door het beeld van de functie op dat punt te berekenen:

\displaystyle f\left(\frac{-b}{2a}\right)

De coördinaten van het hoekpunt van een kwadratische functie (of parabool) zijn dus:

\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)

Snijpunten met de assen van een kwadratische functie

Een parabool snijdt altijd de y-as (Y-as), en dit gebeurt wanneer

x=0.

Om het afkappunt van een kwadratische functie met de Y-as te berekenen, moet men daarom oplossen

f(0).

Het snijpunt met de OY-as van de volgende kwadratische functie is bijvoorbeeld:

f(x)=x^2-2x+1

f(0)=0^2-2\cdot 0+1 = 1

\bm{(0,1)}

Aan de andere kant treedt het afkappunt van een kwadratische functie met de x-as (X-as) op wanneer

f(x)=0.

Om het snijpunt met de X-as te berekenen, moet je dus de vergelijking oplossen

f(x)=0.

Hieronder ziet u als voorbeeld de berekening van het afsnijpunt met de OX-as van dezelfde kwadratische functie:

f(x)=x^2-2x+1

0=x^2-2x+1

We lossen de kwadratische vergelijking op met de algemene formule:

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1

Het snijpunt van de kwadratische functie met de X-as is daarom:

\bm{(1,0)}

In dit geval hadden we maar één oplossing voor de kwadratische vergelijking, maar we hadden twee oplossingen kunnen krijgen. In dit geval betekent dit dat de kwadratische functie de X-as op twee verschillende punten snijdt.

Voorbeeld van weergave van een kwadratische of parabolische functie


Laten we eens kijken hoe we een kwadratische functie in een grafiek kunnen weergeven met behulp van een voorbeeld.

  • Grafiek de volgende functie:

f(x)=x^2-4x+5

Het eerste dat u moet doen, is het hoekpunt van de parabool berekenen. Om dit te doen, gebruiken we de formule die we hierboven zagen:

x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2

Zodra we weten waar het hoekpunt zich zal bevinden, moeten we een tabel met waarden samenstellen:   We berekenen de waarde van de functie op het hoekpunt en op de punten eromheen:

f(x)=x^2-4x+5

  • x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1

  • x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2

  • x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2

  • x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5

  • x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5

\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}

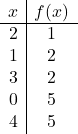
Je kunt ook de snijpunten van de kwadratische functie berekenen met de cartesische assen om de parabool beter te tekenen, maar dit is niet strikt noodzakelijk.

We geven nu de verkregen punten weer in een grafiek :

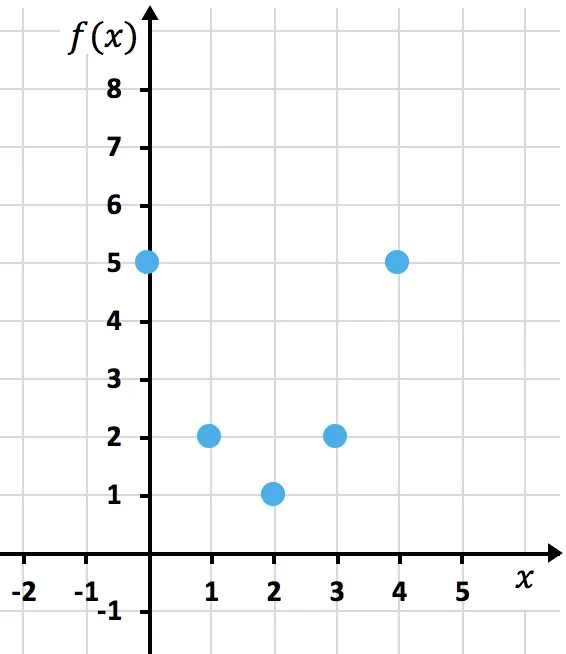
voorbeeld van hoe u een kwadratische of parabolische functie kunt weergeven

En tenslotte voegen we de punten samen die de parabool vormen. Vervolgens verlengen we de takken van de parabool om aan te geven dat deze verder naar boven gaat:

weergave van een kwadratische of parabolische functie

Opgeloste oefeningen over kwadratische functies

Oefening 1

Zoek het hoekpunt van de volgende kwadratische functie:

f(x)=2x^2+8x+4

We berekenen eerst de X-coördinaat van het hoekpunt met behulp van de formule:

x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2

En nu berekenen we de andere coördinaat door de functie op het punt te evalueren:

\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}

Het hoekpunt van de kwadratische functie is daarom:

\bm{(-2,-4)}

Oefening 2


Zoek de afkappunten van de volgende functie met de assen:

f(x)=x^2-4x+3

Om het snijpunt met de Y-as te berekenen, moeten we berekenen

f(0):

f(0)=0^2-4\cdot 0+3 = 3

De functie gaat daarom door de Y-as op het punt:

\bm{(0,3)}

En om de snijpunten met de X-as te vinden, moeten we oplossen

f(x)=0:

f(x)=x^2-4x+3

0=x^2-4x+3

We berekenen de wortels van de kwadratische vergelijking met de formule:

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}

De functie snijdt daarom de X-as op twee punten:

\bm{(1,0) \qquad (3,0)}

Oefening 3

Teken de volgende kwadratische functie:

f(x)=-x^2+4x+1

Dit is een kwadratische functie. Om het weer te geven moet je daarom eerst de abscis van de top van de parabool berekenen met de formule:

x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2

Nu maken we de tabel met waarden. Om dit te doen, berekenen we de waarde van

f(x)

bovenaan en rond de bovenkant:

x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5

x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4

x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4

x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1

x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1

\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}

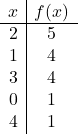
En ten slotte zetten we de punten in de grafiek uit en tekenen we de parabool:

kwadratisch functievoorbeeld

Oefening 4

Teken de volgende kwadratische functie:

f(x)=-2x^2-8x-1

Dit is een tweede orde functie. Om het voor te stellen moet je dus eerst de abscis van het hoekpunt van de parabool vinden met de formule:

x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2

Nu bouwen we de tabel met waarden. Om dit te doen, berekenen we de waarde van

f(x)

bovenaan en rond de bovenkant:

x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7

x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5

x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5

x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1

x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1

\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}

Ten slotte zetten we de punten in de grafiek uit en tekenen we de parabool:

oefening stap voor stap opgelost van kwadratische functie

Oefening 5

Teken de volgende onvolledige kwadratische functie in een grafiek:

f(x)=x^2+2

Het is een polynomiale functie van graad twee. Om het weer te geven moet je daarom eerst de abscis van de top van de parabool berekenen met de formule:

x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0

In dit geval is de functie onvolledig, aangezien deze geen eerstegraadstermijn kent. Daarom

b=0 .

Nu maken we de tabel met waarden. Om dit te doen, berekenen we de waarde van

f(x)

bovenaan en rond de bovenkant:

x= 0 \ \longrightarrow \ f(0)=0^2+2=2

x= 1 \ \longrightarrow \ f(1)=1^2+2=3

x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3

x= 2 \ \longrightarrow \ f(2)=2^2+2=6

x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6

\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}

Ten slotte zetten we de punten in de grafiek uit en tekenen we de parabool:

opgeloste oefeningen om een onvolledige kwadratische functie weer te geven

Oefening 6

Los het volgende probleem met betrekking tot kwadratische functies op:

De productiekosten van een product worden gedefinieerd door de volgende functie:

f(x)=x^2-12x+76

Goud

x

zijn de geproduceerde eenheden (in duizenden) en

f(x)

zijn de productiekosten van de eenheden (in duizenden euro’s).

  • Vertegenwoordigt de productiekostenfunctie in een grafiek.
  • Bepaal hoeveel duizenden eenheden er moeten worden geproduceerd om de kosten te minimaliseren.

Dit is een kwadratische functie. Om het voor te stellen moet je dus eerst de abscis van het hoekpunt van de parabool vinden met de formule:

x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6

Nu maken we de tabel met waarden. Om dit te doen, berekenen we de waarde van

f(x)

bovenaan en rond de bovenkant:

x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40

x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41

x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41

x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44

x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44

\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}

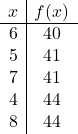
Nu zetten we de punten in de grafiek uit en tekenen we de parabool:

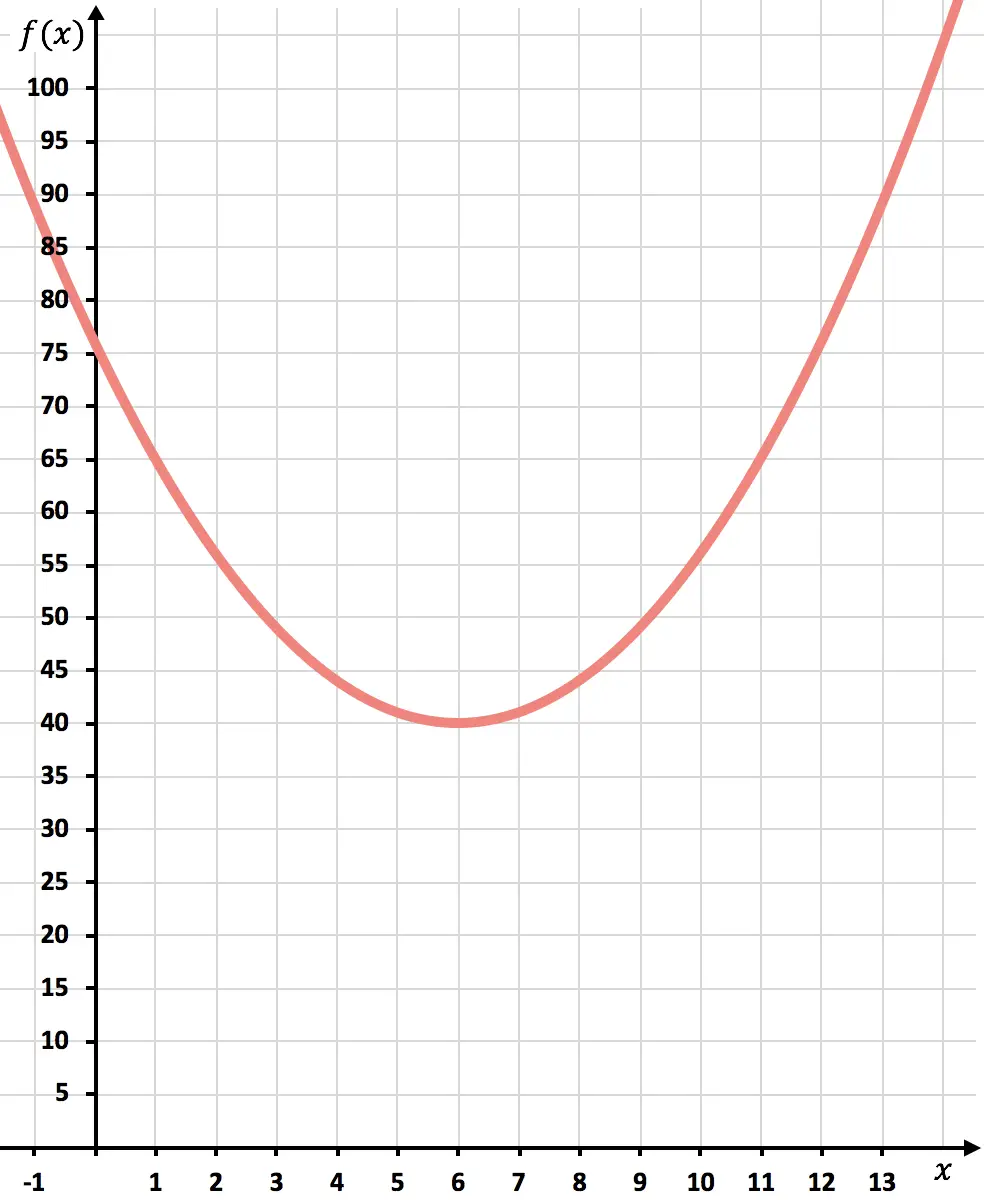
kwadratisch of parabolisch functieprobleem

Zodra de functie is weergegeven, zullen we zien hoeveel de kosten worden geminimaliseerd.

Zoals de grafiek laat zien, worden de minimale kosten bovenaan de parabool bereikt. Omdat dat is waar de functie de kleinste waarde aanneemt.

Concluderend zullen de kosten worden geminimaliseerd door 6.000 eenheden te produceren.

Oefening 7

Los het volgende kwadratische functieprobleem op:

Een atleet voert een speerworp uit waarvan het traject kan worden weergegeven door de volgende functie:

h(x) = -0,025x^2+2x+2

Goud

x

zijn de meters die door de speer worden afgelegd en

h

de hoogte (ook in meters).

Wat is de maximale hoogte die de speer kan bereiken?

Dit is een kwadratische functie, dus het traject van de speer zal een parabool zijn.

Omdat de coëfficiënt van de kwadratische term negatief is (-0,025), zal de parabool bovendien een omgekeerde U-vorm hebben en zullen de takken naar beneden gaan. De speer zal dus bovenaan de maximale hoogte bereiken, aangezien dit het hoogste punt van de parabool zal zijn.

We berekenen daarom de abscis van het hoekpunt van de parabool met de formule:

x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40

En dan berekenen we hoe hoog de speer op dat punt zal zijn door de functie te evalueren

x=40:

h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42

De maximale hoogte die de speer kan bereiken is dus 42 meter.

Oefening 8

Los het volgende probleem met betrekking tot kwadratische functies op:

De productiekosten (in euro’s) van een bedrijf worden gedefinieerd door de volgende functie:

C(q)=40000+20q+q^2

Goud

q

zijn de geproduceerde eenheden.

En de verkoopprijs van elke eenheid is € 520.

  • Hoeveel winst zal het bedrijf maken als het 150 eenheden verkoopt?
  • Hoeveel eenheden moeten worden verkocht voor maximale winst?

Het bedrijf verdient € 520 voor elke verkochte eenheid. Daarom is de functie die het inkomen definieert:

I(q)=520\cdot q = 520q

Goud

q

zijn de verkochte eenheden.

Maar ze vragen ons naar de winst, dat wil zeggen: de inkomsten minus de kosten. We trekken daarom de opbrengsten minus de kosten af om de functie te verkrijgen die de winst van het bedrijf beschrijft:

B(q)=I(q)-C(q)

B(q)=520q - (40000+20q+q^2)

B(q)=520q - 40000-20q-q^2

B(q)=-q^2 + 500q - 40000

Zodra we de functie kennen die de winst van het bedrijf beschrijft, vervangt u eenvoudigweg 150 in de functie-uitdrukking om de winst te berekenen die het bedrijf zal behalen door 150 eenheden te verkopen:

\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}

Door 150 eenheden te verkopen, zal het bedrijf dus een winst van € 12.500 maken.

De verklaring vraagt ons ook om te berekenen met hoeveel eenheden de maximale winst wordt behaald.

De functie die winst beschrijft is een kwadratische functie en heeft dus de vorm van een parabool. En aangezien de coëfficiënt van de kwadratische term negatief is (-1), zal de parabool een omgekeerde U-vorm hebben en zullen de takken naar beneden gaan. Daarom wordt de maximale winst bovenaan behaald, aangezien dit het hoogste punt van de parabool is.

We berekenen daarom de abscis van het hoekpunt van de parabool met de formule:

x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250

Het bedrijf zal dus de maximale winst behalen door 250 eenheden te verkopen.

Aan de andere kant, zelfs als het persbericht er niet om vraagt, kunnen we de winst bepalen die zal worden gemaakt door deze 250 eenheden te verkopen:

B(250) =-(250)^2 + 500\cdot250- 40000= 22500

€


Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven