Kwadraat van een verschil (of aftrekking)

Hier leggen we uit wat de opmerkelijke identiteitsformule van het kwadraat van een verschil (of aftrekking) is, dat wil zeggen, we laten zien hoe de uitdrukking (ab) ² wordt opgelost. Daarnaast kun je voorbeelden zien en oefenen met oefeningen opgelost in het kwadraat van een verschil. En tot slot laten we de formuledemonstratie en geometrische interpretatie van dit opmerkelijke producttype zien.

Wat is het kwadraat van een verschil (of aftrekking)?

Het kwadraat van een verschil , of kwadraat van een aftrekking , is een van de opmerkelijke identiteiten (of opmerkelijke producten), dat wil zeggen dat het bestaat uit een wiskundige regel die de berekening van de kwadratuur van ‘een binominale term met twee termen vergemakkelijkt: één positieve en de ander negatief.

Daarom is de algebraïsche uitdrukking voor het kwadraat van een verschil (ab) ² .

Formule voor het kwadraat van een verschil (of aftrekking)

Zodra we de definitie van dit soort opmerkelijke identiteit hebben gezien, zullen we zien hoe we het kwadraat van een verschil kunnen oplossen met de formule:

Zodat het kwadraat van een verschil gelijk is aan het kwadraat van de eerste term, minus tweemaal het product van de eerste en de tweede, plus het kwadraat van de tweede.

Om een verschil of een kwadratische aftrekking te berekenen, moet je dus niet alleen elke term tot twee verhogen, maar ze ook met elkaar en met 2 vermenigvuldigen.

Dit is belangrijk om te onthouden, omdat een veel voorkomende fout bij het aftrekken van kwadraten is dat je het product niet tussen de twee termen plaatst en alleen het kwadraat van de afname en het aftrekken van de aftrekking oplost:

kwadraat van de binomiaal van een aftrekking

Vergeet het product tussen a en b niet!

Voorbeelden van verschil- (of aftrekkings)vierkanten

Nu we de formule voor het kwadraat van een verschil kennen, kunnen we er berekeningen mee uitvoeren. En zodat je kunt zien hoe dit wordt gedaan, hebben we verschillende opgeloste voorbeelden gemaakt van het kwadraat van een verschil (of aftrekking).

voorbeeld 1

Los het volgende verschil in het kwadraat op:

$(x-3)^2$

Het is een kwadratische aftrekking, dus je moet de formule ervan toepassen:

$(a-b)^2=a^2-2ab+b^2$

We moeten dus identificeren wat de waarden van de onbekenden zijn

$a$

$b$

van de formule. In dit geval,

$a$

is de variabele

$x$

$b$

komt overeen met nummer 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Merk op dat het minteken er geen deel van uitmaakt

$b,$

maar u moet altijd het getal zonder teken nemen om de formule correct toe te passen.

We kennen de waarden dus al van

$a$

en van

$b$

Daarom hoeven we deze waarden alleen in de formule te vervangen:

binominale aftrekkingsoefeningen in het kwadraat opgelost

Voorbeeld 2

Bereken de volgende binomiaal van een kwadratische aftrekking:

$(5x-2)^2$

De formule voor het kwadraat van het verschil is:

$(a-b)^2=a^2-2ab+b^2$

We moeten dus eerst de waarden van identificeren

$a$

en van

$b$

van de formule. Bij dit probleem

$a$

vertegenwoordigt het monomiaal

$5x$

$b$

is equivalent aan de onafhankelijke term van de binominale term, dat wil zeggen 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

Eindelijk, zodra we de waarde van de parameters kennen

$a$

$b$

, passen we eenvoudigweg de binomiale formule toe voor kwadratische aftrekking:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

Bewijs van de formule voor het kwadraat van een verschil

We zullen dan afleiden waar de formule voor het kwadraat van een aftrekking vandaan komt. Hoewel je het bewijs niet hoeft te onthouden, is het toch leuk om de wiskunde erachter te begrijpen.

Als we uitgaan van de uitdrukking van de binominale waarde van alle aftrekkingen:

$(a-b)^2$

Het is duidelijk dat de vorige macht gelijk is aan het product van de factor

$(a-b)$

vermenigvuldigd met zichzelf:

$(a-b)^2= (a-b)\cdot (a-b)$

Nu vermenigvuldigen we de twee haakjes door de distributieve eigenschap toe te passen:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

En we hoeven alleen maar vergelijkbare termen te groeperen om de formule te bewijzen:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Om de formule voor het kwadraat van een aftrekking wiskundig te bewijzen:

$(a-b)^2=a^2-2ab+b^2$

Uit curiositeit wordt de uitbreiding van de binomiale uitdrukking van een kwadratische aftrekking ook wel een perfect vierkante trinominaal genoemd.

Geometrische interpretatie van het kwadraat van een verschil

Om het begrip van het kwadraat van een verschil te voltooien, zullen we zien hoe we deze opmerkelijke gelijkheid geometrisch kunnen interpreteren.

Kijk naar het volgende vierkant met zijden met lengte

$a:$

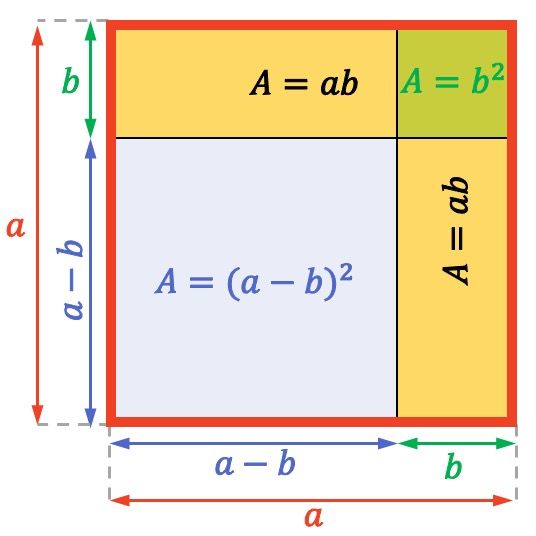
geometrische interpretatie van het kwadraat van een verschil

De oppervlakte (of oppervlakte) van een vierkant of rechthoek wordt berekend door twee aangrenzende zijden te vermenigvuldigen. Daarom is de oppervlakte van het gehele gehele vierkant hierboven

$a\cdot a = a^2.$

Op dezelfde manier is de oppervlakte van elke gele rechthoek gelijk aan

$a\cdot b = ab.$

En ten slotte heeft het kleine vierkant rechtsboven een oppervlakte van

$b\cdot b =b^2.$

Dit betekent dat een vierkant van zijde

$(a-b),$

waarvan het oppervlak is

$(a-b)^2,$

kan worden ontleed in de oppervlakte van een vierkant van afmeting

$a,$

minus 2 maal de oppervlakte van een rechthoek met afmetingen

$a$

$b$

, plus de oppervlakte van een zijvierkant

$b.$

Kortom, de formule voor het kwadraat van een verschil kan ook geometrisch worden geverifieerd:

$(a-b)^2=a^2-2ab+b^2$

Opgeloste problemen van het kwadraat van een verschil (of aftrekking)

Zodat je kunt oefenen, laten we je een aantal oefeningen achter die stap voor stap zijn opgelost op het opmerkelijke product van het kwadraat van een verschil. Vergeet niet dat u ons al uw vragen hieronder in de opmerkingen kunt schrijven.

Oefening 1

Los de volgende aftrekkingen in het kwadraat op:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

zie oplossing

Om alle opmerkelijke identiteiten van het probleem te vinden, volstaat het om de formule voor het kwadraat van een verschil toe te passen, namelijk:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

Oefening 2

Bepaal de volgende kwadraten van de verschillen tussen twee grootheden door de formule toe te passen:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

zie oplossing

Om alle opmerkelijke producten van het probleem te bepalen, is het noodzakelijk om de formule voor een kwadratische aftrekking te gebruiken:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

Om sectie B op te lossen, moet je onthouden dat als een wortel in het kwadraat is, deze vereenvoudigd is:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

De monomialen van de laatste kwadratische aftrekking hebben breukcoëfficiënten, dus om dit op te lossen moeten we de eigenschappen van breuken gebruiken:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

Wat is het kwadraat van een verschil (of aftrekking)?

Formule voor het kwadraat van een verschil (of aftrekking)

Voorbeelden van verschil- (of aftrekkings)vierkanten

voorbeeld 1

Voorbeeld 2

Bewijs van de formule voor het kwadraat van een verschil

Geometrische interpretatie van het kwadraat van een verschil

Opgeloste problemen van het kwadraat van een verschil (of aftrekking)

Oefening 1

Oefening 2

Laat een reactie achter Reactie annuleren