Op deze pagina vind je de formule voor het kwadraat van een som, dat wil zeggen de opmerkelijke identiteit (a+b) 2 . Je zult ook voorbeelden en opgeloste oefeningen van kwadratische sommen kunnen zien. En bovendien ontdekt u de geometrische eigenschappen die verborgen liggen in dit opmerkelijke product.
Wat is het kwadraat van een som?
Het kwadraat van een som is een van de opmerkelijke identiteiten (of opmerkelijke producten), dus het is een wiskundige regel waarmee je snel de macht van een binomiaal met twee kwadratische positieve termen kunt berekenen.
Het kwadraat van een som bestaat dus uit twee verschillende termen die bij elkaar zijn opgeteld en gekwadrateerd, dat wil zeggen dat de algebraïsche uitdrukking voor het kwadraat van een som (a+b) 2 is.
Formule voor het kwadraat van een som
Gegeven de wiskundige definitie van dit opmerkelijke type identiteit, zullen we nu zien wat de formule voor het kwadraat van een som is:

Zodat het kwadraat van een som gelijk is aan het kwadraat van de eerste term, plus tweemaal het product van de eerste door de tweede, plus het kwadraat van de tweede.
Om een som in het kwadraat op te lossen, is het dus niet voldoende om elke optelling tot twee te verhogen, maar bovendien moeten de twee optellingen met elkaar en met 2 worden vermenigvuldigd.
Dit is belangrijk om te onthouden, omdat een veel voorkomende fout bij het optellen van de vierkanten is dat je het product tussen de twee termen vergeet en alleen de vierkanten berekent:

Vergeet niet om geen termen uit de formule weg te laten!
Aan de andere kant, onthoud dat de formule voor een kwadratische aftrekking (of het kwadraat van een aftrekking) sterk lijkt op degene die we zojuist hebben gezien, maar er is een verschil dat het resultaat volledig verandert. Als je niet zeker weet hoe dat eruit ziet, kun je hier kijken wat de kwadratische aftrekkingsformule is en hoe deze wordt toegepast.
Voorbeelden van somkwadraten
Hier volgen enkele praktische voorbeelden, zodat u kunt zien hoe u een som kwadrateerd:
voorbeeld 1
- Bereken de volgende som in het kwadraat door de formule toe te passen:
![]()
De formule voor een kwadratische som is:
![]()
We moeten eerst de parameters identificeren
![]()
En
![]()
van de formule. In dit geval,
![]()
vertegenwoordigt de
![]()
van het paar en
![]()
komt overeen met nummer 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Nou ja, aangezien we nu de waarden kennen van
![]()
en van
![]()
We kunnen de formule toepassen om het resultaat van het kwadraat van de som te vinden:

Voorbeeld 2
- Los de volgende uitdrukking op voor het kwadraat van een som:
![]()
De formule voor het kwadraat van een som is:
![]()
Dus bij dit probleem
![]()
is het monomiaal
![]()
En aan de andere kant,
![]()
is de onafhankelijke term 4:
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
Eindelijk, zodra we de waarden van hebben geïdentificeerd
![]()
en van
![]()
, passen we de kwadratische somformule toe om het opmerkelijke product op te lossen:
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
Bewijs van de formule voor het kwadraat van een som
Vervolgens leiden we de formule die we zojuist hebben gezien af uit het kwadraat van een som, zodat je begrijpt waar deze vandaan komt.
Beginnend met een positieve binomiaal verhoogd naar 2:
![]()
De bovenstaande macht is uiteraard gelijk aan de factor
![]()
vermenigvuldigd met zichzelf:
![]()
We vermenigvuldigen dus de twee haakjes met behulp van de distributieve eigenschap:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Ten slotte groeperen we uit de resulterende termen de termen die vergelijkbaar zijn:
![]()
En we zijn al aangekomen bij de polynoomuitdrukking van de formule, dus het is bewezen:
![]()
Hoewel het misschien moeilijk te geloven is, werkt het kwadraat van een somformule ook voor het ontbinden van kwadratische polynomen . Voor het geval u niet weet wat het is: polynoomontbinden is een procedure die in de wiskunde vaak wordt gebruikt om de uitdrukking van een polynoom te vereenvoudigen. Ontdek hoe u dat doet door op de bovenstaande link te klikken.
Geometrische interpretatie van het kwadraat van een som
Tot nu toe hebben we gezien hoe het kwadraat van een som wiskundig wordt berekend, maar dit opmerkelijke product kan ook geometrisch worden geïnterpreteerd.
Kijk naar het volgende vierkant waarvan de zijden even groot zijn
![]()
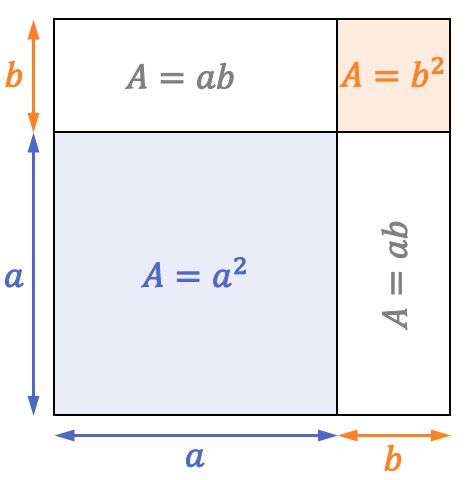
De oppervlakte van een vierkant is gelijk aan de lengte van een van de zijden in het kwadraat. Daarom is de zijde van het vorige vierkant hetzelfde
![]()
het gebied (of oppervlak) is gelijk aan
![]()
Zoals je kunt zien in de vierkante weergave, is een vierkant met een oppervlakte van
![]()
rechthoeken met twee vlakken
![]()
en nog een vierkant oppervlak
![]()
Daarom wordt vanuit geometrisch oogpunt ook voldaan aan de formule voor de som van een vierkant:
![]()
Opgeloste problemen van het kwadraat van een som
Vervolgens laten we u stap voor stap een aantal opgeloste kwadratensommen-oefeningen achter, zodat u kunt oefenen en zo het concept kunt begrijpen. U kunt al uw vragen in de opmerkingen stellen, wij beantwoorden ze graag. 💭💭💭
Oefening 1
Bepaal de volgende bedragen in het kwadraat:
![]()
![]()
![]()
![]()
Om alle opmerkelijke identiteiten van het probleem op te lossen, volstaat het om de formule voor het kwadraat van een som toe te passen:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Oefening 2
Los de volgende somkwadraten van twee termen op door de formule toe te passen:
![]()
![]()
![]()
Om alle opmerkelijke producten van het probleem te berekenen, moet je de formule voor een kwadratische som gebruiken:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
In sectie B) moet je onthouden dat als een wortel in het kwadraat is, deze vereenvoudigd is:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
De monomialen van de laatste som in het kwadraat hebben breukcoëfficiënten, dus om dit op te lossen moeten we ook de eigenschappen van breuken gebruiken:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Oefening 3
Vind de volgende macht door de formule voor het kwadraat van een som toe te passen en zonder de rekenmachine te gebruiken:
![]()
Allereerst kan het getal zeventien worden opgesplitst in de som van 10 plus 7:
![]()
Dus hebben we het vermogen omgerekend naar een kwadraatsom. Daarom kunnen we nu de overeenkomstige formule toepassen:
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
Kort gezegd is het resultaat van potentiëring:
![]()
Zoals je in deze oefening hebt gezien, is de somkwadraatformule ook handig voor het berekenen van machten van grote getallen zonder een rekenmachine te gebruiken.
Kwadraat van een som van 3 termen
Soms komen we erachter dat we het kwadraat van drie opgetelde termen moeten oplossen, dat wil zeggen (a+b+c) 2 . Logischerwijs kunnen we in deze gevallen de formule die we hebben uitgelegd niet gebruiken, omdat we tussen haakjes een trinominaal hebben in plaats van een binomiaal. Het is daarom noodzakelijk om een andere formule te gebruiken.
De formule voor het kwadraat van de som van 3 termen is als volgt:
![]()
Laten we eens kijken hoe deze formule wordt toegepast aan de hand van een voorbeeld:
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
Zoals u kunt zien, maakt het toevoegen van één element aan de formule het resultaat veel gecompliceerder.