▷ Bereken het kruisproduct van twee vectoren (voorbeelden)

Op deze pagina wordt uitgelegd wat het kruisproduct van twee vectoren is en hoe dit wordt berekend. U zult ook zien hoe u de richting en richting van het kruisproduct kunt vinden met behulp van de rechterhandregel (of kurkentrekker). En bovendien vindt u de toepassingen van dit soort operaties, evenals voorbeelden, oefeningen en problemen die stap voor stap worden opgelost.

Wat is het kruisproduct van twee vectoren?

In de wiskunde is het kruisproduct een bewerking tussen twee vectoren in een driedimensionale ruimte (in R3). Het resultaat van deze vectorbewerking is een vector met een richting loodrecht op de twee vermenigvuldigde vectoren, en met een module gelijk aan het product van de modules van de vermenigvuldigingsvectoren door de sinus van de hoek die ze vormen. Met andere woorden, de formule is:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

Zoals je in de vorige formule ziet, wordt het kruisproduct aangegeven

$\bm{\times}$

, daarom wordt het ook kruisproduct genoemd. Het wordt ook wel het Gibbs-vectorproduct genoemd, omdat hij het heeft uitgevonden.

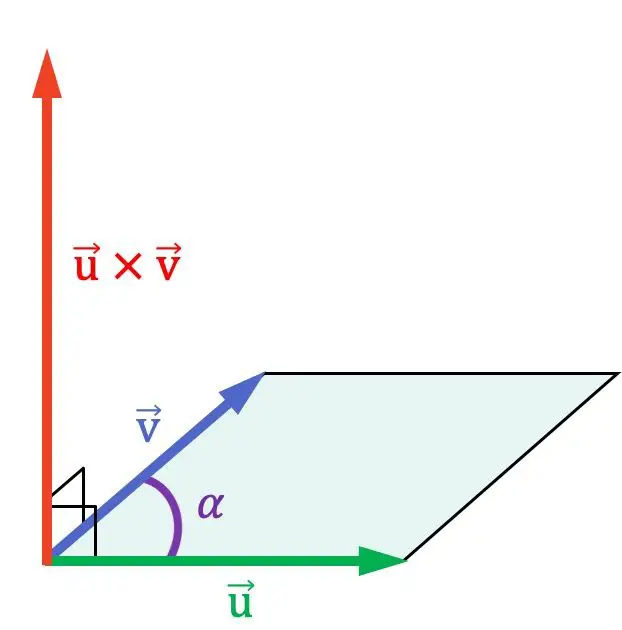
Zoals je in de vorige grafische weergave kunt zien, staat het kruisproduct loodrecht op de twee vectoren die ze vermenigvuldigen en is het daarom normaal voor het vlak dat ze bevat.

Formule voor het berekenen van het kruisproduct van twee vectoren

Als we de cartesische coördinaten van de vectoren kennen, is de eenvoudigste manier om hun kruisproduct te berekenen het oplossen van een 3×3 determinant. Bekijk hoe het moet:

Beschouw twee willekeurige vectoren:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Het vectorproduct is:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

Waar de vectoren

$\vv{i}, \vv{j},\vv{k}$

Dit zijn de eenheidsvectoren in respectievelijk de X-, Y- en Z-asrichting.

Laten we een voorbeeld bekijken van hoe u het kruisproduct tussen twee vectoren kunt berekenen:

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

Om het vectorproduct tussen de vectoren te bepalen, moeten we de volgende determinant van orde 3 maken:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

In dit geval zullen we de determinant oplossen met behulp van adjuvantia of cofactoren (de Sarrus-regel kan ook worden gebruikt):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

Het resultaat van het vectorproduct van de twee vectoren is daarom:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

Bepaalt de richting en richting van het kruisproduct

Soms hoeven we de componenten van de vector die het resultaat zijn van het kruisproduct niet te kennen, maar het is voldoende om de module, de richting en de richting ervan te vinden. Dit gebeurt vaak in de natuurkunde, vooral bij de berekening van krachten.

Er zijn dus verschillende regels voor het vinden van de richting en richting van het vectorproduct, de bekendste zijn de rechterhandregel , met drie vingers of met de hele hand, en de kurkentrekkerregel (of de schroef) . Je kunt ze allemaal gebruiken, je hoeft ze dus niet allemaal te kennen. We leggen je toch de drie regels uit, zodat je je kunt houden aan degene die je het leukst vindt. 😉

Rechterhandregel (3 vingers)

De drievingerige versie van de rechterhandregel of -wet omvat het uitvoeren van de volgende stappen:

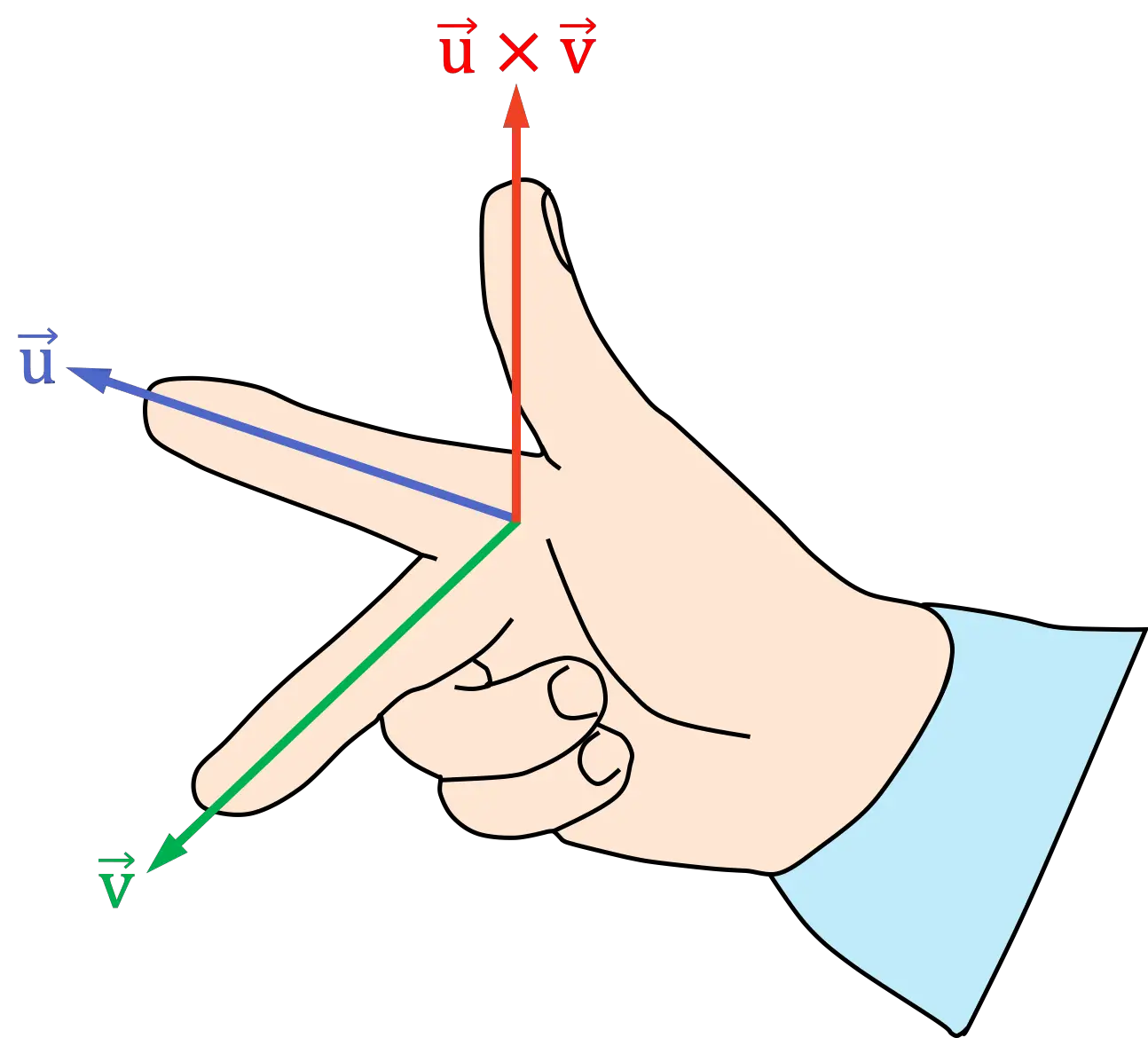
Plaats de wijsvinger van uw rechterhand in de richting van de eerste vector van het kruisproduct
$(\vv{\text{u}}).$
Plaats de middelvinger (of middelvinger) van uw rechterhand in de richting van de tweede vector van het kruisproduct
$(\vv{\text{v}}).$
De resulterende duimpositie geeft de richting en richting van het kruisproduct aan
$(\vv{\text{u}}\times\vv{\text{v}}).$

Rechterhandregel (handpalm)

De palmaire versie van de rechterhandregel of wet lijkt sterk op de vorige regel. Om het toe te passen, moet u de volgende stappen volgen:

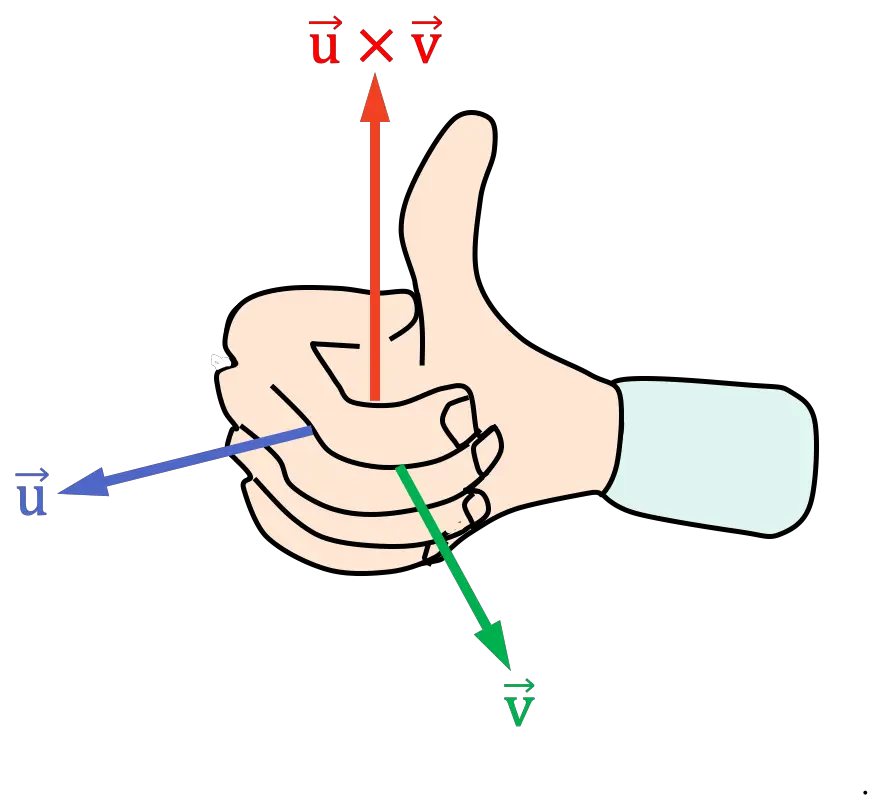
Plaats uw rechterhand en wijs met uw vingers in dezelfde richting als de eerste vector van het kruisproduct
$(\vv{\text{u}}).$
Sluit uw rechterhand door uw vingers naar de tweede vector van het kruisproduct te bewegen
$(\vv{\text{v}}).$

Je moet je hand sluiten aan de kant waar de hoek (of afstand) tussen de vectoren kleiner is.
De resulterende positie van de duim bepaalt de richting van het kruisproduct
$(\vv{\text{u}}\times\vv{\text{v}}).$

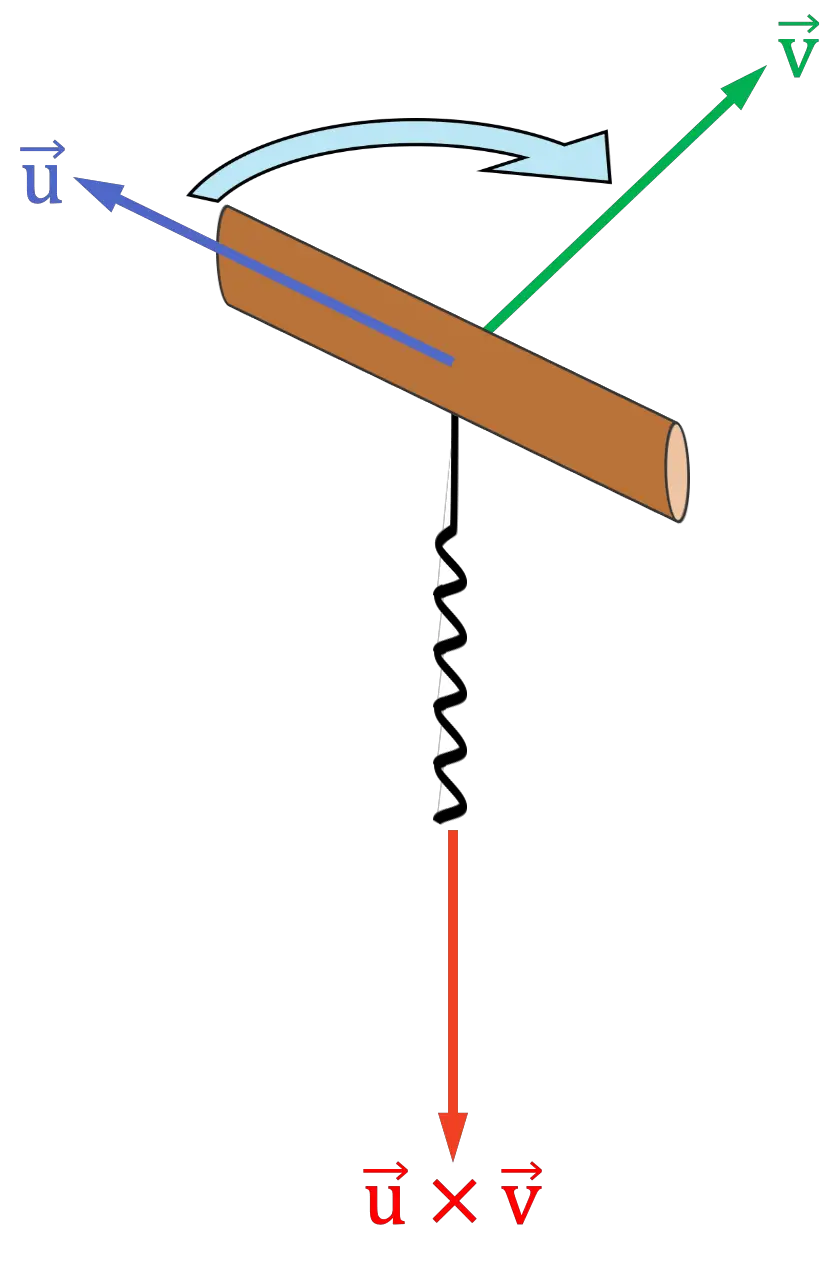
kurketrekkerregel

De kurkentrekker- of schroefregel is vergelijkbaar met de rechterhandregel, waarbij de hele handpalm wordt gebruikt. De procedure is als volgt:

Gebruik je fantasie en plaats een kurkentrekker (of schroef) met de hendel in dezelfde richting als de eerste vector van het kruisproduct.
$(\vv{\text{u}}).$
Draai vervolgens de kurkentrekker naar de tweede vector van het kruisproduct
$(\vv{\text{v}})$

alsof je het in een kurk zou stoppen. Je moet de kurkentrekker naar de kant draaien waar de afstand tussen de vectoren het kortst is.
De richting waarin de kurkentrekkerspiraal wijst, zal de richting en richting van het vectorproduct zijn
$(\vv{\text{u}}\times\vv{\text{v}}).$

Eigenschappen van het kruisproduct van twee vectoren

Het kruisproduct van twee vectoren heeft de volgende kenmerken:

Anticommutatieve eigenschap: de volgorde van de vectoren die betrokken zijn bij het vectorproduct is niet onverschillig, omdat het teken afhankelijk daarvan varieert.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

Distributieve eigenschap met betrekking tot het optellen en aftrekken van vectoren:

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

Homogene eigenschap : het vermenigvuldigen van een vector van het kruisproduct met een scalair (een reëel getal) komt overeen met het vermenigvuldigen van het resultaat van het kruisproduct met de genoemde scalair.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

De vector die voortkomt uit het vectorproduct staat loodrecht op de twee vectoren die bij de operatie betrokken zijn.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

Als de twee vectoren bovendien orthogonaal zijn, wordt aan de volgende vergelijkingen voldaan:

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

Het kruisproduct van twee parallelle vectoren is gelijk aan de nulvector (of nul).

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

Als we de hoek die door twee vectoren wordt gevormd niet kennen, kan de modulus van hun vectorproduct ook worden berekend met behulp van de volgende uitdrukking:

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

Bereken de oppervlakte van een parallellogram of driehoek met behulp van het kruisproduct

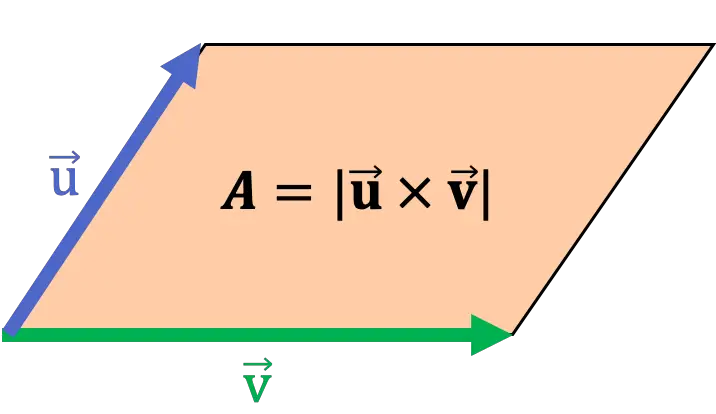
Geometrisch valt de modulus van het kruisproduct van twee vectoren samen met het gebied van het parallellogram dat deze twee vectoren als zijden heeft. Daarom kan het kruisproduct worden gebruikt om de oppervlakte van een parallellogram te berekenen.

kruisproduct van twee vectoren in de ruimte

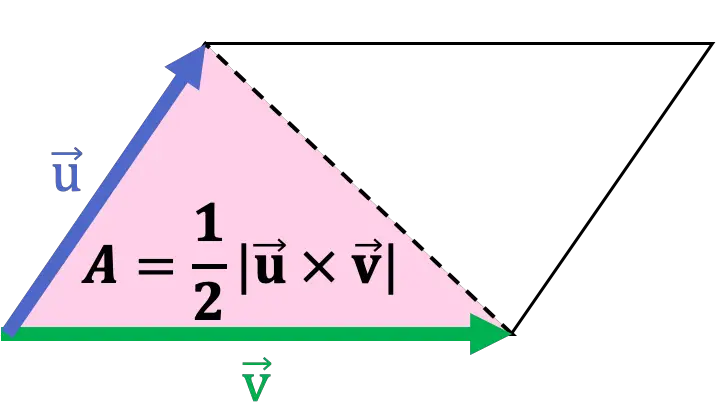
Bovendien verdeelt de diagonaal van een parallellogram het in twee driehoeken, of met andere woorden: een driehoek is de helft van een parallellogram. De oppervlakte van een driehoek is dus de helft van de modulus van het kruisproduct, waarbij twee zijden als vectoren worden genomen.

Bedenk dat de modulus van een vector in een driedimensionale ruimte de wortel is van de som van de kwadraten van zijn coördinaten:

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Dit zijn twee van de toepassingen van het kruisproduct van twee vectoren op het gebied van de wiskunde. Het heeft echter nog andere toepassingen, bijvoorbeeld in de natuurkunde wordt het gebruikt om het magnetische veld te berekenen.

Opgeloste oefeningen over vectorproducten van vectoren

Oefening 1

Bereken het kruisproduct tussen de volgende twee vectoren:

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

Zie de oplossing

Om het vectorproduct tussen de vectoren te bepalen, moeten we de volgende determinant van dimensie 3×3 oplossen:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

In dit geval zullen we de determinant oplossen met behulp van adjuvantia of cofactoren (maar de Sarrus-regel kan ook worden gebruikt):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

Het resultaat van het vectorproduct van de twee vectoren is daarom:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

Oefening 2

Zoek het kruisproduct tussen de volgende twee vectoren:

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

Zie de oplossing

Om het vectorproduct tussen de twee vectoren te vinden, moeten we de volgende 3×3 determinant oplossen:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

In dit geval zullen we de determinant oplossen met behulp van adjuncten of cofactoren (hoewel de regel van Sarrus door elkaar kan worden gebruikt):

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

Het resultaat van het vectorproduct tussen de twee vectoren is daarom:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

Oefening 3

De modules van twee vectoren kennen en de hoek die ze vormen:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

Bepaal de grootte van het kruisproduct van de twee vectoren.

Zie de oplossing

We kunnen eenvoudig de modulus van het vectorproduct tussen de twee vectoren berekenen door de formule toe te passen:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

Oefening 4

Van de volgende vectoren in het schermvlak:

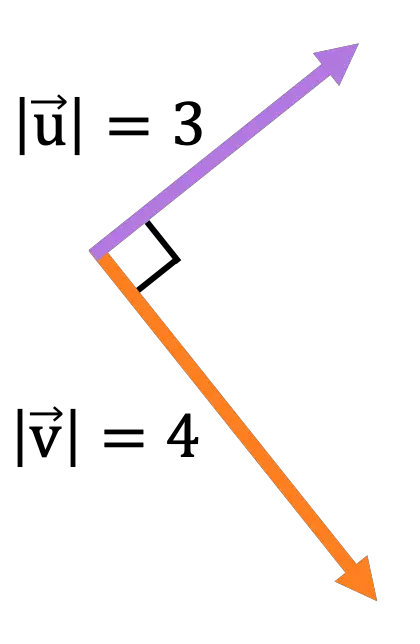
Bereken de grootte, richting en betekenis van de vector die resulteert uit de volgende vectorbewerking:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

Zie de oplossing

De twee vectoren staan loodrecht, dus de norm van het vectorproduct is:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

Aan de andere kant staat de vector die voortkomt uit het vectorproduct loodrecht op de twee vectoren die aan de bewerking deelnemen; de richting ervan zal daarom loodrecht op het scherm staan.

En ten slotte kunnen we met behulp van de rechte lijnregel (of kurkentrekkerregel) afleiden dat de richting van de resulterende vector naar de binnenkant van het scherm zal zijn.

Oefening 5

Bereken de oppervlakte van het parallellogram met de volgende vectoren als twee zijden:

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

Zie de oplossing

Het gebied van een parallellogram valt samen met de modulus van het kruisproduct van de vectoren waaruit het bestaat. We berekenen daarom het vectorproduct van de vectoren:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

En dan je module:

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

Oefening 6

Zoek het gebied van de driehoek waarvan de hoekpunten de volgende punten zijn:

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

Zie de oplossing

Allereerst moeten we de vectoren berekenen die de zijden van de driehoek vormen:

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

De oppervlakte van een driehoek is de helft van de grootte van het vectorproduct van de vectoren waaruit deze driehoek bestaat. We berekenen daarom het vectorproduct van de vectoren:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

Na je module:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

En ten slotte zal het gebied van de driehoek de helft van de module zijn:

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

Kruisproduct van twee vectoren (of kruisproduct)

Wat is het kruisproduct van twee vectoren?

Formule voor het berekenen van het kruisproduct van twee vectoren

Bepaalt de richting en richting van het kruisproduct

Rechterhandregel (3 vingers)

Rechterhandregel (handpalm)

kurketrekkerregel

Eigenschappen van het kruisproduct van twee vectoren

Bereken de oppervlakte van een parallellogram of driehoek met behulp van het kruisproduct

Opgeloste oefeningen over vectorproducten van vectoren

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Laat een reactie achter Reactie annuleren