▷ Afgeleide van de cosinus (formule en opgeloste oefeningen)

Hier ontdekt u hoe u de cosinusfunctie (formule) kunt afleiden. Je kunt voorbeelden zien van afgeleiden van cosinusfuncties en oefenen met stapsgewijze oefeningen. Daarnaast laten we u het bewijs van de formule zien, wat de tweede afgeleide van de cosinus is en zelfs de afgeleide van de inverse cosinus.

Wat is de afgeleide van de cosinus?

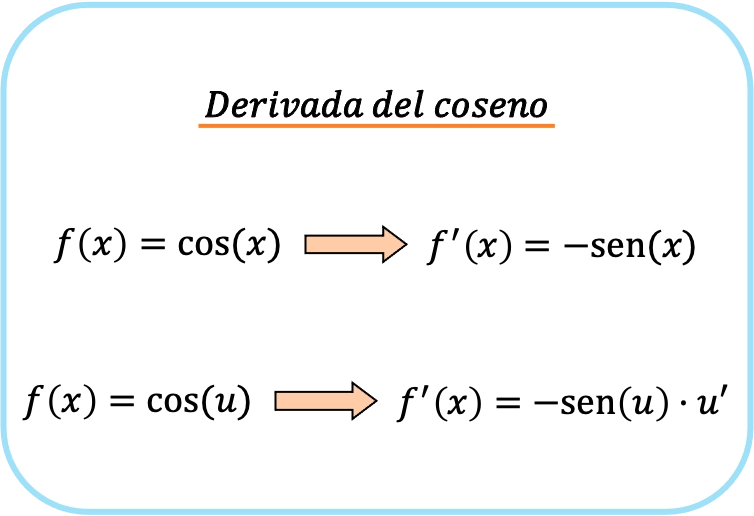
De afgeleide van de cosinusfunctie is de teken-gemodificeerde sinusfunctie. Met andere woorden: de afgeleide van de cosinus van x is gelijk aan minus de sinus van x.

$f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)$

Als er een functie in het cosinusargument aanwezig is, is de afgeleide van de cosinus het product van minus de sinus van die functie maal de afgeleide van de functie.

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

De tweede formule is gelijk aan de eerste formule, maar met toepassing van de kettingregel. Samenvattend is de formule voor de afgeleide van de cosinus dus als volgt:

Cosinus afgeleide voorbeelden

Nu we weten wat de cosinusformule is, zullen we verschillende voorbeelden van dit soort trigonometrische afgeleiden uitleggen, zodat je geen twijfels meer hebt over hoe je de cosinusfunctie kunt afleiden.

Voorbeeld 1: Afgeleide van de cosinus van 2x

$f(x)=\text{cos}(2x)$

In het cosinusargument hebben we geen enkele x, maar eerder een complexere functie. Daarom moeten we de volgende formule gebruiken om de cosinus af te leiden:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Omdat de afgeleide van 2x 2 is, zal de afgeleide van de cosinus van 2x minus de sinus van 2x vermenigvuldigd met 2 zijn.

$f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)$

Voorbeeld 2: Afgeleide van de cosinus van x kwadraat

$f(x)=\text{cos}(x^2)$

Net als in het vorige voorbeeld hebben we in het cosinusargument een andere functie dan x, dus zullen we de kettingregel gebruiken om de cosinus af te leiden:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Dan is de afgeleide van x ² 2x, daarom is de afgeleide van de cosinus van x verheven tot de macht 2:

$f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x$

Voorbeeld 3: Afgeleide van de gekubeerde cosinus

$f(x)=\text{cos}^3(2x^6-5x^3)$

De cosinusfunctie in dit voorbeeld bestaat uit een andere functie, dus we moeten de volgende formule toepassen om de afgeleide op te lossen:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Door de formule toe te passen komen we dus tot de afgeleide van de functie:

$\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}$

➤ Om deze functie te differentiëren, moet je ook de formule voor de afgeleide van een potentiële functie gebruiken.

Tweede afgeleide van de cosinus

Vervolgens zullen we zien dat de tweede afgeleide van de sinus eenvoudig kan worden berekend, dankzij de kenmerken van trigonometrische functies.

➤ Opmerking: Om het volgende te begrijpen, moet je weten wat de afgeleide van sinus is .

De tweede afgeleide van de cosinus van x is minus de cosinus van x. Dit lijkt misschien vreemd, maar wiskundig gezien is het zo. De afgeleide van de sinus is inderdaad de cosinus en daarom wordt, door de cosinus van x tweemaal te differentiëren, opnieuw de cosinus verkregen, maar met een aangepast teken.

$\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}$

Deze eigenschap verandert als het cosinusargument niet x is, omdat we in dit geval de term van de kettingregel verslepen:

$\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}$

Afgeleide van inverse cosinus

Alle trigonometrische functies hebben een inverse functie en als zodanig kan de cosinusfunctie ook worden omgekeerd. Op dezelfde manier is de inverse cosinus differentieerbaar.

De afgeleide van de inverse cosinus van een functie is minus de afgeleide van de functie gedeeld door de vierkantswortel van één minus het kwadraat van de functie.

$f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Bedenk dat de inverse cosinus ook wel arccosinus wordt genoemd.

De afgeleide van de inverse cosinus van 3x is bijvoorbeeld:

$f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}$

Opgeloste oefeningen over de afgeleide van de cosinus

Bereken de afgeleide van de volgende cosinusfuncties:

$\text{A) } f(x)=\text{cos}(4x)$

$\text{B) } f(x)=\text{cos}(2x^3-5x+1)$

$\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)$

$\text{D) } f(x)=\text{cos}^5(x^2+3x)$

$\text{E) } f(x)=\text{cos}\left(e^{5x}\right)$

$\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)$

Zie de oplossing

$\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)$

$\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)$

$\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)$

$\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)$

$\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}$

$\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}$

Bewijs van de cosinusafgeleide

Ten slotte zullen we wiskundig de formule demonstreren voor de afgeleide van de cosinus van x. Om dit te doen, zullen we de definitie van de afgeleide gebruiken, die overeenkomt met de volgende limiet:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

We gaan de cosinus bewijzen, dus de functie is cos(x):

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x+h)-\text{cos}(x)}{h}$

We kunnen deze grens niet oplossen door vervanging, omdat we dan in onbepaaldheid terecht zouden komen. We kunnen de cosinus van een som echter op een andere manier uitdrukken door de volgende trigonometrische identiteit toe te passen:

$\text{cos}(a+b)=\text{cos}(a)\text{cos}(b)-\text{sen}(a)\text{sen}(b)$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\text{cos}(h)-\text{sen}(x)\text{sen}(h)-\text{cos}(x)}{h}$

De volgende stap is om de breuk in twee breuken te verdelen en de gemeenschappelijke factor van de cosinus te nemen:

$\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]$

De limiet van een aftrekking is gelijk aan de aftrekking van de limieten, dus:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\lim_{h \to 0}\frac{\text{sen}(x)\text{sen}(h)}{h}$

De cosinus van x en de sinus van x zijn niet afhankelijk van h, dus we kunnen ze buiten de grenzen halen:

$\displaystyle f'(x)=\text{cos}(x)\lim_{h \to 0}\frac{\text{cos}(h)-1}{h}-\text{sen}(x)\lim_{h \to 0}\frac{\text{sen}(h)}{h}$

Door de berekening van limieten met oneindig kleine equivalenten te gebruiken, concluderen we dat de eerste limiet 0 is en de tweede limiet 1. Daarom:

$\displaystyle f'(x)=\text{cos}(x)\cdot 0-\text{sen}(x)\cdot 1$

$\displaystyle f'(x)=-\text{sen}(x)$

En we hebben de formule voor de afgeleide van de cosinusfunctie al bereikt, dus de gelijkheid is bewezen.

Wat is de afgeleide van de cosinus?

Cosinus afgeleide voorbeelden

Voorbeeld 1: Afgeleide van de cosinus van 2x

Voorbeeld 2: Afgeleide van de cosinus van x kwadraat

Voorbeeld 3: Afgeleide van de gekubeerde cosinus

Tweede afgeleide van de cosinus

Afgeleide van inverse cosinus

Opgeloste oefeningen over de afgeleide van de cosinus

Bewijs van de cosinusafgeleide

Laat een reactie achter Reactie annuleren