De kleinste kwadratenmethode is een wiskundig hulpmiddel voor het vinden van de beste rechte lijn die overeenkomt met een reeks punten . Wij leggen het u eenvoudig uit:
Stel je voor dat je een aantal punten in een grafiek hebt die hier en daar verspreid zijn. U wilt een rechte lijn vinden die het beste bij deze punten past, zodat de afstand tussen de lijn en de punten zo klein mogelijk is . Dit is het idee achter de kleinste kwadratenmethode.
De methode gebruikt een formule om de vergelijking van de lijn te berekenen die de som van de kwadraten van de verschillen tussen de punten en de lijn minimaliseert. Dat wil zeggen, er wordt gezocht naar de lijn met de kleinste “afwijking” ten opzichte van de punten.
Simpel gezegd is de kleinste kwadratenmethode nuttig voor de analyse van gegevens die tijdens een onderzoek zijn verkregen, met als doel hun gedrag op een lineaire manier uit te drukken, waardoor de fouten van de gestolen informatie worden verminderd.
Wie heeft de kleinste kwadratenmethode bedacht?
De kleinste kwadratenmethode, een fundamenteel hulpmiddel in de statistiek en data-analyse, wordt toegeschreven aan de Duitse wiskundige Carl Friedrich Gauss , die deze in 1794 voorstelde. Gauss publiceerde deze echter pas in 1809 .
Interessant is dat de Franse wiskundige Andrien-Marie Legendre in 1805 een soortgelijke versie publiceerde en deze onafhankelijk ontwikkelde.
Beide wiskundigen hebben geholpen bij het creëren van deze methode, die in verschillende disciplines op grote schaal wordt gebruikt om modellen aan te passen aan waargenomen gegevens en nauwkeurige voorspellingen te doen.
kleinste kwadraten formule
Om te begrijpen wat deze methode inhoudt, is het ongetwijfeld essentieel om de formule en het implementatieproces ervan uit te leggen. Hier is een gedetailleerde uitleg van de kleinste kwadratenformule:
definieer het probleem
Stel dat u een gegevensset heeft met twee variabelen, een onafhankelijke variabele (x) en een afhankelijke variabele (y), en u wilt een rechte lijn op deze gegevens aansluiten.
Het doel is om de waarden van de coëfficiënten van de vergelijking van de lijn (snijpunt en helling) te vinden, waardoor de som van de kwadraten van de verschillen tussen de werkelijke waarden van y en de waarden die worden voorspeld door de ingerichte lijn.
Bereken de vergelijking van de lijn
De vergelijking van een lijn heeft de vorm y = mx + b, waarbij m de helling is en b het y-snijpunt. De kleinste kwadratenformule voor het berekenen van myb-waarden is:
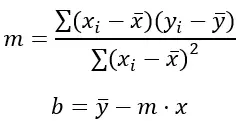
Goud:
Σ vertegenwoordigt de som van de waarden.
x i en y i zijn de waarden van respectievelijk de variabelen x en y voor elk gegevenspunt.
x̄ en ȳ zijn de gemiddelden van respectievelijk de waarden van x en y.
(x i – x̄) en (y i – ȳ) zijn de verschillen tussen de waarden van x en y en hun respectievelijke gemiddelden.
(x i – x̄) 2 is het kwadraat van het verschil tussen de waarde van x en het gemiddelde ervan.
interpreteer de resultaten
Nadat u de waarden van m en b met behulp van de formule hebt berekend, kunt u deze gebruiken om de vergelijking van de gepaste lijn te verkrijgen. Als je bijvoorbeeld m = 2 en b = 3 hebt, dan is de vergelijking van de gepaste lijn y = 2x + 3. Hiermee kun je voorspellingen of schattingen maken van de y-waarden voor verschillende waarden van x op basis van het aangepaste recht.
Wanneer wordt de kleinste kwadratenmethode gebruikt?
U zult zich waarschijnlijk afvragen: wanneer wordt deze methode gebruikt? Het is erg handig in verschillende situaties! Bijvoorbeeld wanneer u experimentele of onderzoeksgegevens wilt analyseren om een relatie of trend te vinden .
Stel dat u de relatie onderzoekt tussen de prijs van een huis en de oppervlakte ervan in vierkante meters. Je kunt de kleinste kwadratenmethode gebruiken om de rechte lijn te vinden die het beste bij de gegevens past en die je een duidelijk beeld geeft van deze relatie.
Het wordt ook in de economie gebruikt om variabelen zoals productvraag of prijsgedrag te modelleren en voorspellen . Bovendien wordt in de techniek de kleinste kwadratenmethode toegepast om wiskundige modellen aan te passen aan test- of simulatiegegevens.
De kleinste kwadratenmethode is een krachtig en veelzijdig hulpmiddel dat in veel studie- en werkgebieden wordt gebruikt om gegevens te analyseren en belangrijke relaties te vinden.
Toepassingen van de kleinste kwadratenmethode in andere stellingen
Naast het gebruik ervan op zichzelf, is de kleinste kwadratenmethode ook zeer nuttig in andere stellingen. Laten we hieronder wat meer over dit onderwerp bekijken.
Regressiestelling
Het wordt veel gebruikt in de regressiestelling om de beste lijn te vinden die bij een reeks gegevens past . Je kunt het bijvoorbeeld gebruiken om de relatie tussen de hoogte van een plant en de hoeveelheid licht die hij ontvangt te analyseren om te bepalen hoe de plant zal groeien onder verschillende lichtomstandigheden.
Stelling interpolatie
In dit geval wordt de kleinste kwadratenmethode ook toegepast in de interpolatiestelling om de polynoomfunctie te vinden die het beste bij een reeks punten past. U kunt het bijvoorbeeld gebruiken om het traject van een bewegend object te schatten op basis van positie- en tijdgegevens.
Curve-fitting-stelling
Het wordt gebruikt in de curve-fitting-stelling om een curve te vinden die bij een reeks gegevens past . Dit is handig bij toepassingen zoals het modelleren van klimaatgegevens om klimaatverandering te voorspellen of om het traject van een projectiel te voorspellen.
Fourieranalyse-stelling
In de Fourier-analysestelling wordt de kleinste kwadratenmethode gebruikt om een periodieke functie te benaderen uit een reeks discrete gegevens . Dit geldt voor datasignalering en beeld- en geluidscompressie.
Niet-lineaire regressiestelling
Ten slotte wordt de kleinste kwadratenmethode ook toegepast in de niet-lineaire regressiestelling om de beste curve te vinden die past bij een dataset die geen lineaire relatie volgt . U kunt het bijvoorbeeld gebruiken om te analyseren hoe de concentratie van een chemische stof de reactiesnelheid beïnvloedt.
Voorbeeld van de kleinste kwadratenmethode
Om beter te begrijpen hoe u de kleinste kwadratenmethode kunt toepassen, bekijken we hieronder een voorbeeld.
Stel dat je de volgende hoogtegegevens (in centimeters) hebt van een plant in verschillende weken:
| Week | hoogte in centimeters |
| 1 | tien |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | twintig |
Je wilt de beste rechte lijn vinden die bij deze gegevens past, zodat je een voorspelling kunt doen van de toekomstige planthoogte.
Stap 1 : Maak een grafiek van de gegevens
Het eerste dat u moet doen, is de gegevens in een spreidingsdiagram plotten. De x-as vertegenwoordigt weken en de y-as vertegenwoordigt de hoogte in centimeters. Hier is de grafiek:
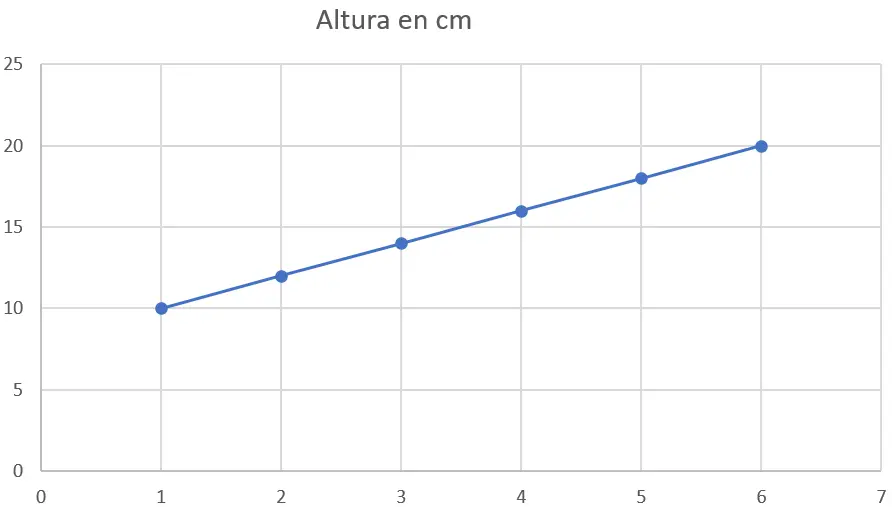
Stap 2 : Pas de kleinste kwadratenmethode toe
De kleinste kwadratenmethode probeert een lijn te vinden die de som van de kwadraten van de verschillen tussen de werkelijke gegevens en de door de lijn voorspelde waarden minimaliseert. In dit geval wordt de lijn weergegeven door de vergelijking van een lijn: y = mx + b, waarbij “y” de hoogte is, “x” de weken, “m” de helling van de lijn en “b” de het y-snijpunt.
Om de waarden van “m” en “b” te vinden die de som van de kwadraten van de verschillen minimaliseren, worden de volgende formules gebruikt:
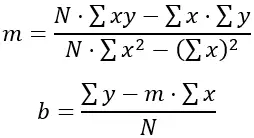
Waar N het aantal gegevenspunten is (in dit geval 6), is Σxy de som van weken maal de hoogten, Σx is de som van weken, Σy is de som van hoogten en Σx 2 is de som van kwadraten van weken .
Door deze formules op de hoogtegegevens toe te passen, verkrijgen we:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Deze waarden vervangen door de formules voor “m” en “b”:
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Daarom is de vergelijking van de rechte lijn die overeenkomt met de hoogtegegevens: y.