Hessische matrix (of Hessen) -

Deze pagina is zeker de meest complete uitleg van de Hessische matrix die er bestaat. Hier wordt het concept van de Hessische matrix uitgelegd, hoe je deze kunt berekenen met voorbeelden en er zijn zelfs verschillende opgeloste oefeningen om te oefenen. Bovendien kunt u leren hoe de maximale en minimale waarden van een multivariabele functie worden berekend, en of het een concave of convexe functie is. En tot slot vindt u ook de Hessische matrixhulpprogramma’s en -toepassingen.

Wat is de Hessische matrix?

De definitie van de Hessische (of Hessische) matrix is als volgt:

De Hessische matrix is een vierkante matrix met dimensie n × n, samengesteld uit de gedeeltelijke tweede afgeleiden van een functie van n variabelen.

Deze matrix wordt ook wel Hessisch genoemd, of wordt in sommige wiskundeboeken zelfs Discriminant genoemd. Maar de meest gebruikelijke manier om het te noemen is de Hessische matrix.

De formule voor de Hessische matrix is daarom als volgt:

Daarom zal de Hessische matrix altijd een vierkante matrix zijn waarvan de dimensie gelijk zal zijn aan het aantal variabelen in de functie. Als de functie bijvoorbeeld drie variabelen heeft, heeft de Hessische matrix de dimensie 3×3.

Bovendien zegt de stelling van Schwarz (of de stelling van Clairaut) dat de volgorde van differentiatie er niet toe doet, dat wil zeggen dat ze eerst gedeeltelijk worden afgeleid met betrekking tot de variabele

$x_1$

dan met betrekking tot de variabele

$x_2$

komt neer op gedeeltelijk differentiëren met betrekking tot

$x_2$

respecteer dan

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

Daarom is de Hessische matrix een symmetrische matrix, of met andere woorden, hij heeft een symmetrie waarvan de as de hoofddiagonaal is.

Uit curiositeit is de Hessische matrix vernoemd naar Ludwig Otto Hesse, een 19e-eeuwse Duitse wiskundige die zeer belangrijke bijdragen heeft geleverd op het gebied van lineaire algebra.

Voorbeeld van het berekenen van de Hessische matrix

Laten we een voorbeeld bekijken van hoe we een Hessische matrix met dimensie 2 × 2 kunnen vinden:

Bereken de Hessische matrix op het punt (1,0) van de volgende functie:

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

Eerst moeten we de partiële afgeleiden van de eerste orde berekenen:

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

Zodra we de eerste afgeleiden al kennen, berekenen we alle partiële afgeleiden van de tweede orde:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

Daarom kunnen we nu de Hessische matrix vinden uit de formule voor 2 × 2 matrices:

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

De Hessische matrix geëvalueerd op het punt (1,0) zal dus zijn:

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

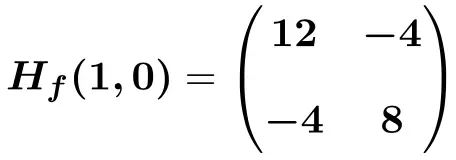
Problemen van Hessische matrices opgelost

Oefening 1

Bereken de Hessische matrix van de volgende functie met 2 variabelen op het punt (1,1):

$\displaystyle f(x,y)=x^2y+y^2x$

zie oplossing

Eerst moeten we de partiële afgeleiden van de eerste orde van de functie vinden:

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

Nadat we de eerste afgeleiden al hebben berekend, gaan we verder met het oplossen van alle partiële afgeleiden van de tweede orde:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

De Hessische matrix wordt dus als volgt gedefinieerd:

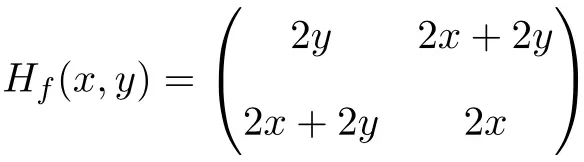
Opgeloste oefening van de Hessische of Hessische matrix van dimensie 2x2

Ten slotte hoeft u alleen nog maar de Hessische matrix op punt (1,1) te evalueren:

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

Oefening 2

Bereken de Hessiaan op het punt (1,1) van de volgende functie in twee variabelen:

$\displaystyle f(x,y)= e^{y\ln x}$

zie oplossing

Eerst moeten we de partiële afgeleiden van de eerste orde van de functie berekenen:

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

Zodra we de eerste afgeleiden hebben, berekenen we de partiële afgeleiden van de tweede orde van de functie:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

De Hessische matrix van de functie is dus een vierkante matrix met dimensie 2 × 2:

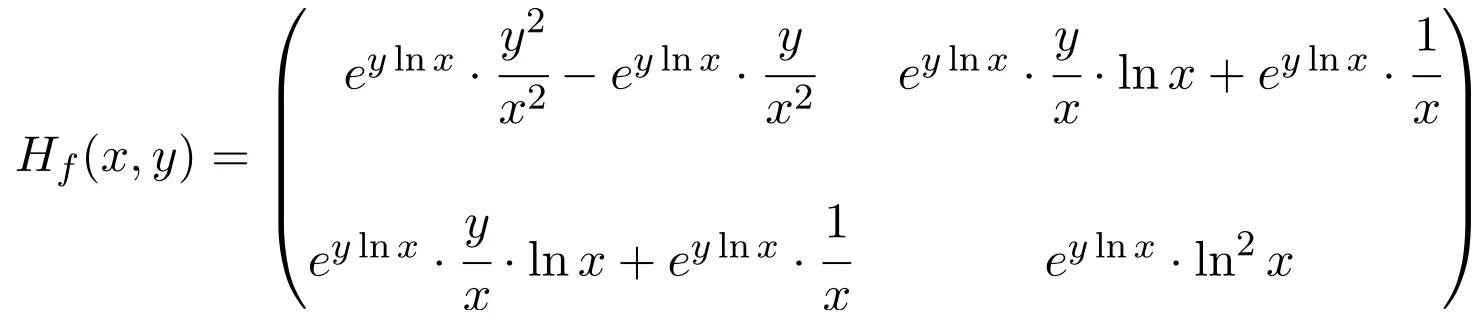
Opgeloste Hessische oefening of Hessische matrix van dimensie 2x2

Ten slotte hoeft u alleen nog maar de Hessische matrix op punt (1,1) te evalueren:

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Oefening 3

Zoek de Hessische matrix op het punt

$(0,1,\pi)$

van de volgende functie met 3 variabelen:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

zie oplossing

Eerst berekenen we de partiële afgeleiden van de eerste orde van de functie:

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

Zodra we de eerste afgeleiden hebben, berekenen we de partiële afgeleiden van de tweede orde van de functie:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

Zodat de Hessische matrix van de functie een vierkante matrix is met dimensie 3×3:

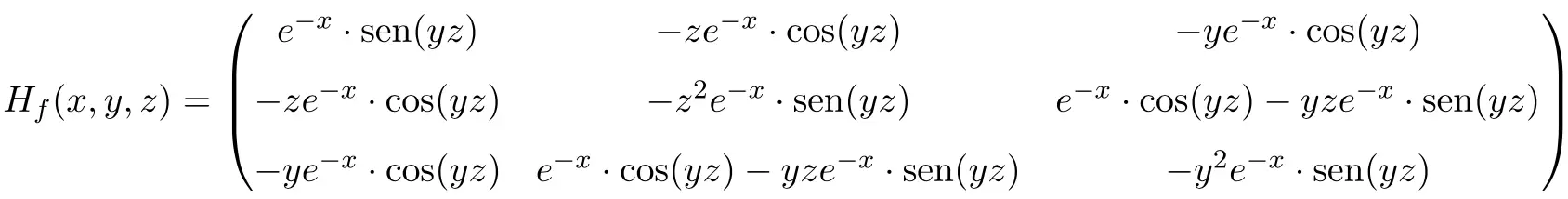
voorbeeld van jute of jutematrix met afmeting 3x3

Ten slotte vervangen we de variabelen op het punt door hun respectieve waarden

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

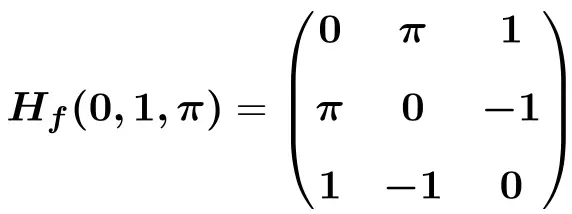
oefening stap voor stap opgelost van Hessische of Hessische matrix van dimensie 3x3

Oefening 4

Bepaal de Hessische matrix op het punt (2,-1,1,-1) van de volgende functie met 4 variabelen:

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

zie oplossing

De eerste stap is het vinden van de partiële afgeleiden van de eerste orde van de functie:

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

Nu lossen we de partiële afgeleiden van de tweede orde van de functie op:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

De uitdrukking van de 4×4 Hessische matrix verkregen door het oplossen van alle partiële afgeleiden is dus als volgt:

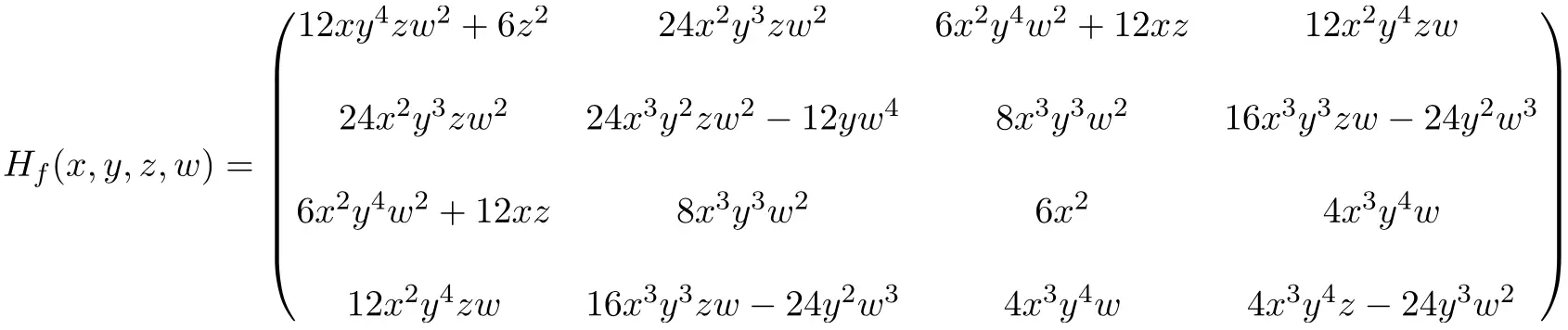
voorbeeld stap voor stap opgelost van jute of jutematrix van afmeting 4x4

Ten slotte vervangen we de onbekenden door hun respectievelijke puntwaarden (2,-1,1,-1) en voeren we de berekeningen uit:

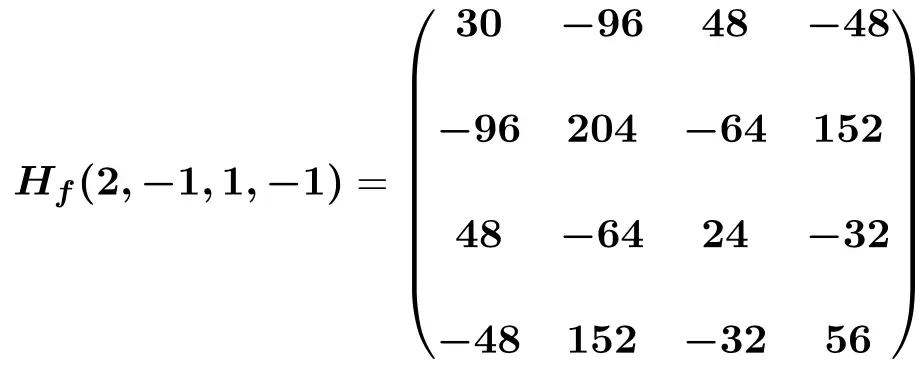
Oefening stap voor stap opgelost van Hessische of Hessische matrix van dimensie 4x4

Hoe weet je of de Hessische matrix positief, negatief of onbepaald is?

Zoals we later zullen zien, is het erg nuttig om te weten of de Hessische matrix een positieve semi-definitieve, positief definitieve, negatieve semi-definitieve, negatief definitieve of onbepaalde matrix is. Laten we eens kijken hoe we erachter kunnen komen:

Criterium van eigenwaarden (of eigenwaarden)

Een manier om te weten welk type matrix het is, is door de eigenwaarden (of eigenwaarden) van de Hessische matrix te doorlopen:

De Hessische matrix is positief semi-definitief als deze eigenwaarden (of eigenwaarden) gelijk aan en groter dan nul heeft. Dat wil zeggen, het heeft positieve eigenwaarden en minstens één gelijk aan 0:

$\lambda \geq 0$

De Hessische matrix is positief definitief als al zijn eigenwaarden (of eigenwaarden) uitsluitend groter zijn dan 0 (positief):

$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li> De Hessische matrix is <span style=$ negatief semi-definitief als deze eigenwaarden (of eigenwaarden) gelijk aan en kleiner dan nul heeft. Dat wil zeggen, het heeft negatieve eigenwaarden en minstens één gelijk aan 0:

$\lambda \leq 0$

De Hessische matrix is negatief definitief als al zijn eigenwaarden (of eigenwaarden) kleiner zijn dan 0 (negatief):

$\lambda < 0$

De Hessische matrix is ongedefinieerd als deze positieve en negatieve eigenwaarden (of eigenwaarden) heeft:

$\lambda > 0 \qquad \lambda <0$

Sylvester-criterium

Een andere manier om te weten welk type de Hessische matrix is, is door het criterium van Sylvester te gebruiken, hoewel deze stelling ons alleen laat weten of deze positief definitief, negatief definitief of onbepaald is. Maar soms kan het veel sneller in gebruik zijn, omdat de berekeningen over het algemeen eenvoudiger zijn.

Het Sylvester-criterium luidt dus als volgt:

Als alle hoofdminoren van de Hessische matrix groter zijn dan 0, is er sprake van een positief definitieve matrix.

Als de belangrijkste minors van de Hessische matrix met even index groter zijn dan 0 en die met oneven index kleiner dan 0, is het een negatief definitieve matrix.

Als alle hoofdminoren van de Hessische matrix niet-0 zijn en aan geen van de voorgaande twee voorwaarden is voldaan, is er sprake van een onbepaalde matrix.

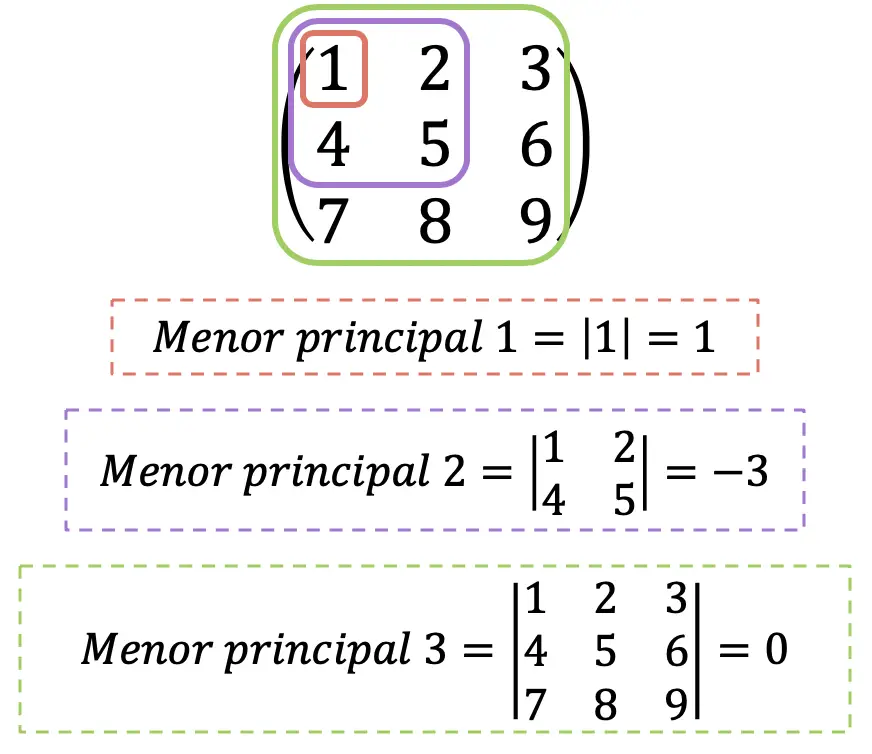
Het is duidelijk dat de maximale hoofdmineur van de Hessische matrix altijd samenvalt met zijn determinant. Uitsluitend voor informatieve doeleinden wordt de determinant van de Hessische matrix ook wel “de Hessische” genoemd, hoewel we dat hier niet zullen doen om verwarring te voorkomen.

Hoe u een maximum of minimum van een functie kunt berekenen met de Hessische matrix

Als u eenmaal weet hoe u de Hessische matrix moet berekenen, vraagt u zich waarschijnlijk af: en waar wordt deze matrix voor gebruikt?

Welnu, een van de toepassingen van de Hessische matrix is het vinden van het maximum of minimum van een functie met meer dan één variabele. Hier volgt een stapsgewijze uitleg over het berekenen van maxima en minima:

Eerst worden de kritische punten van de multivariabele functie berekend. Om dit te doen, berekenen we de gradiënt of de Jacobiaanse matrix van de functie, stellen deze gelijk aan 0 en lossen de vergelijkingen op.
De Hessische matrix wordt berekend.
De kritische punten gevonden in stap 1 worden vervangen door de Hessische matrix. We zullen dus zoveel Hessische matrices verkrijgen als kritische punten de functie hebben.
We kijken welk type matrix elke Hessische matrix is. Dat wil zeggen, we kijken of het positief definitief, negatief definitief, onbepaald, enz. is.
- Als de Hessische matrix positief definitief is, is het kritische punt een relatief minimum van de functie.
- Als de Hessische matrix negatief definitief is, is het kritische punt een relatief maximum van de functie.
- Als de Hessische matrix ongedefinieerd is, is het kritische punt een zadelpunt .

Voorbeeld van het berekenen van maxima en minima van een multivariabele functie

Om te zien hoe dit wordt gedaan, volgt hier een voorbeeld van het berekenen en classificeren van de relatieve extrema van een functie met behulp van de Hessische matrix:

Vind alle relatieve extrema van de volgende multivariabele functie:

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

Het eerste dat we moeten doen is de Jacobiaanse matrix van de functie berekenen, die in dit geval zal samenvallen met de gradiënt omdat het een scalaire functie is:

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

We moeten nu de kritische punten bepalen, hiervoor stellen we de verkregen vergelijkingen gelijk aan 0 en lossen we het stelsel vergelijkingen op:

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

Het kritische punt dat we hebben gevonden is dus (0,-2).

Zodra het kritieke punt van de functie is gevonden, moeten we de Hessische matrix berekenen:

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

En uiteraard is de Hessische matrix die op het kritieke punt wordt geëvalueerd, dezelfde:

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Om te zien welk type matrix het is, gebruiken we het Sylvester-criterium. We lossen daarom de belangrijkste minoren van de matrix op:

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

Hoofdmineur 1 (oneven) is positief en hoofdmineur 2 (even) is negatief, dus volgens het criterium van Sylvester is het een onbepaalde matrix. En daarom is het kritieke punt (0,-2) een zadelpunt.

Het bepalen van de concaviteit of convexiteit van een functie met de Hessische matrix

Een ander gebruik van de Hessische matrix is om te weten of een functie concaaf of convex is. En dit kan worden bepaald volgens de volgende stelling:

Zijn

$A \subseteq \mathbb{R}^n$

een open set en

$f \colon A \to \mathbb{R}$

een functie waarvan de tweede afgeleiden continu zijn, de concaviteit en convexiteit worden gedefinieerd door de Hessische matrix:

Functie
$f$

is overal convex

$A$

dan en slechts dan als de Hessische matrix op elk punt van de verzameling positief semi-definitief is.
Functie
$f$

is overal strikt convex

$A$

dan en slechts dan als de Hessische matrix op elk punt van de verzameling positief definitief is.

✓ Daarom, als

$f$

is een convexe functie op een punt waar de Jacobiaanse matrix ook verdwijnt, dit punt is een lokaal minimum .

Functie
$f$

is over het algemeen hol

$A$

dan en slechts dan als de Hessische matrix op elk punt van de verzameling negatief semi-definitief is.
Functie
$f$

is over het geheel genomen strikt concaaf

$A$

dan en slechts dan als de Hessische matrix op elk punt van de verzameling negatief definitief is.

✓ Daarom, als

$f$

is een functie concaaf op een punt waar de Jacobiaanse matrix ook verdwijnt, dit punt is een lokaal maximum .

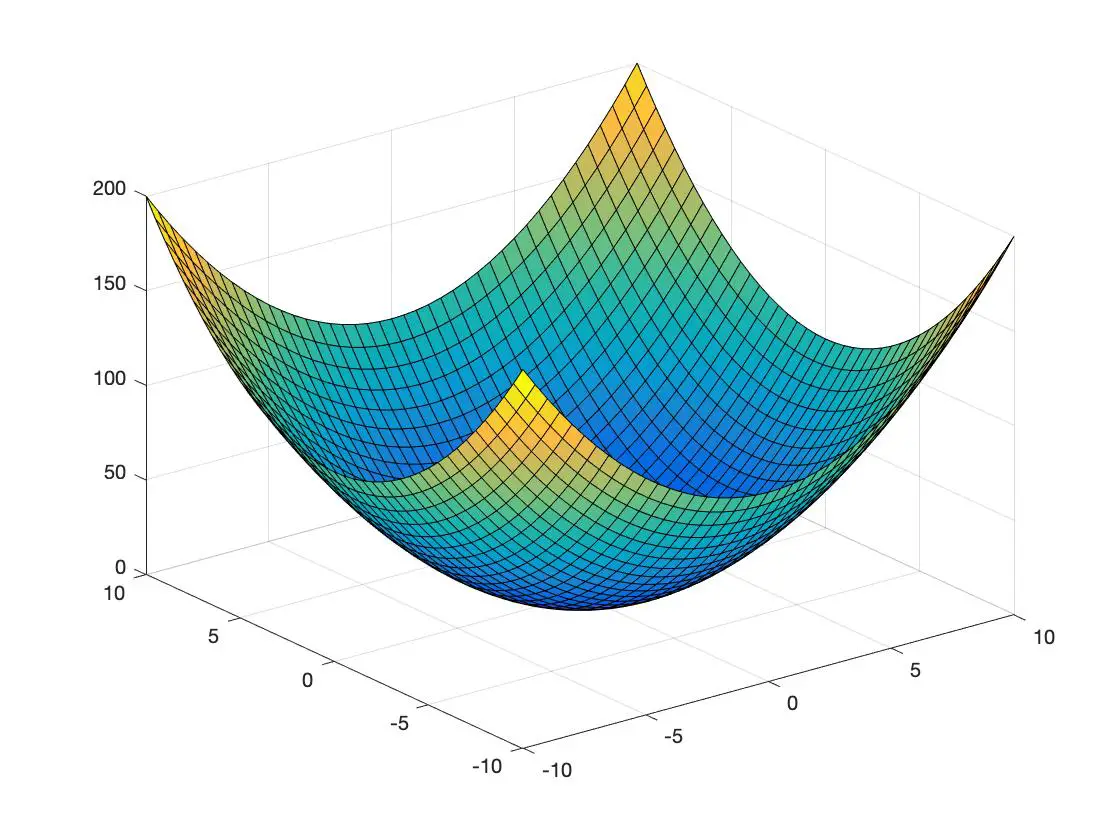
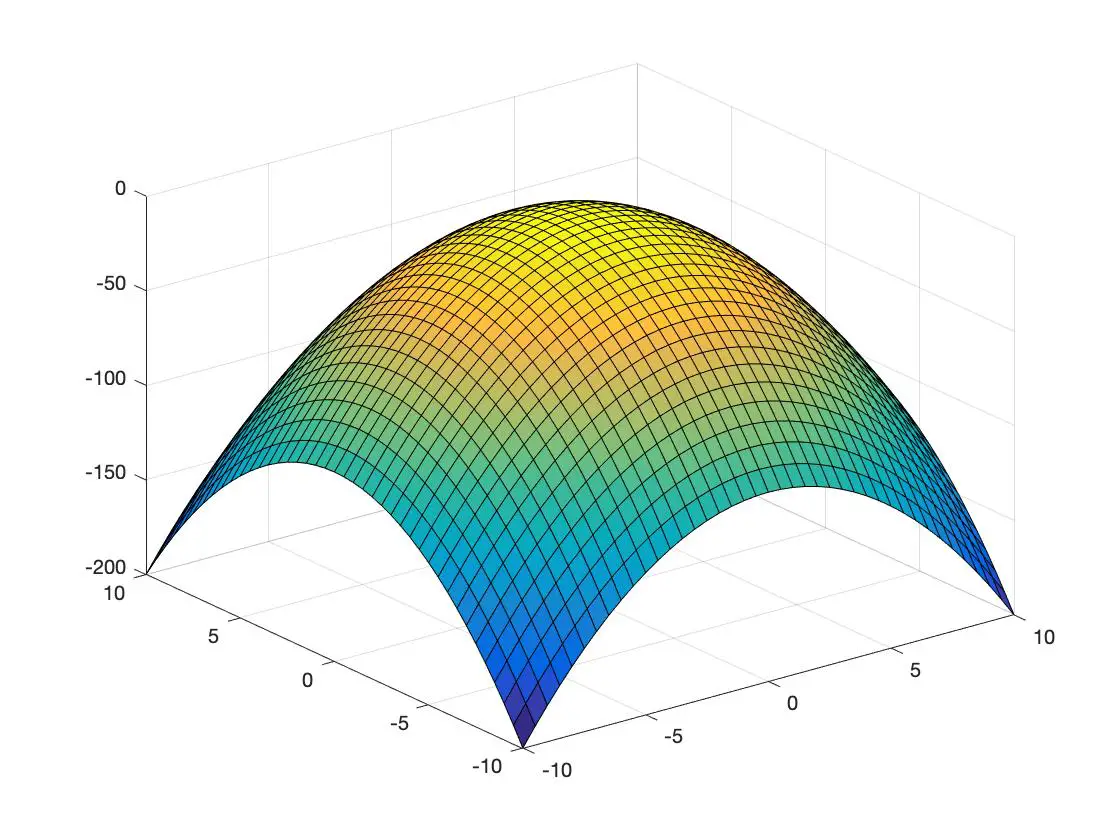
Hieronder heb je een voorbeeld van een convexe functie en een ander van een concave functie weergegeven in een driedimensionale ruimte:

convexe functie

concave functie

De afbeelding heeft een leeg ALT-attribuut; de bestandsnaam is concaviteit-en-convexiteit-van-een-functie-met-de-jute-matrix-1024x768.jpg

Meer toepassingen van de Hessische matrix

De belangrijkste toepassingen van de Hessische matrix zijn de toepassingen die we al hebben gezien, maar er zijn ook andere toepassingen. Voor de meest nieuwsgierigen leggen we ze hieronder uit.

Taylor-polynoom

De uitbreiding van het Taylor-polynoom voor functies van 2 of meer variabelen op het punt

$a$

begint als volgt:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

Zoals je kunt zien, worden de termen van de tweede orde van de Taylor-expansie gegeven door de Hessische matrix, geëvalueerd op het punt van expansie van de polynoom.

Omrande jutematrix

Een ander gebruik van de Hessische matrix is het berekenen van de minima en maxima van een multivariate functie

$f(x,y)$

beperkt tot een andere rol

$g(x,y)$

. Om dit probleem op te lossen wordt de begrensde Hessische matrix gebruikt en wordt de volgende procedure gevolgd:

Stap 1: De Lagrange-functie wordt berekend, die wordt gedefinieerd door de volgende uitdrukking:

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

Stap 2: De kritieke punten van de Lagrange-functie worden gevonden. Om dit te doen, berekenen we de gradiënt van de Lagrange-functie, stellen we de vergelijkingen gelijk aan 0 en lossen we de vergelijkingen op.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

Stap 3: Voor elk gevonden punt berekenen we de begrensde Hessiaan, die wordt gedefinieerd door de volgende matrix:

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

Stap 4: Per kritisch punt bepalen we of het een maximum of een minimum is:

Dit is een lokaal maximum van de functie
$f$

onder functiebeperkingen

$g$

als de laatste nm (waarbij n het aantal variabelen is en m het aantal beperkingen), hebben de belangrijkste minors van de omzoomde Hessische matrix die op het kritieke punt wordt geëvalueerd, afwisselende tekens, beginnend met het negatieve teken.

Dit zal een lokaal minimum van de functie zijn
$f$

onder functiebeperkingen

$g$

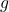
als de laatste nm (waarbij n het aantal variabelen is en m het aantal beperkingen), hebben de belangrijkste minoren van de scherpe Hessiaanse matrix die op het kritieke punt worden geëvalueerd allemaal negatieve tekens.

Houd er rekening mee dat de relatieve minima of maxima van de ene beperkte functie ten opzichte van de andere niet noodzakelijkerwijs zo hoeven te zijn voor de onbeperkte functie. De omrande Hessische matrix is daarom alleen bruikbaar voor dit soort problemen.

Relatie met andere operaties

Ten slotte is de Hessische matrix ook gekoppeld aan andere belangrijke bewerkingen of matrices, voornamelijk met de Jacobiaanse matrix en met de Laplace-operator.

Relatie met de Jacobiaanse matrix

De Hessische matrix van een functie

$f$

is de Jacobiaanse matrix van de gradiënt van dezelfde functie:

$\displaystyle H_f = J(\nabla f)$

Laplace-operator

Het Hessische matrixtracé is equivalent aan de Laplace-operator :

$\displaystyle tr( H_f) = \Delta f$

Deze gelijkheid kan gemakkelijk worden bewezen, aangezien de definitie van de Laplace-operator de divergentie van de gradiënt van een functie is:

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

De uitdrukking ervan is daarom:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

En deze som is slechts het spoor van de Hessische matrix, dus de gelijkwaardigheid is bewezen.

Hessische matrix (of hessen)

Wat is de Hessische matrix?

Voorbeeld van het berekenen van de Hessische matrix

Problemen van Hessische matrices opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Hoe weet je of de Hessische matrix positief, negatief of onbepaald is?

Criterium van eigenwaarden (of eigenwaarden)

Sylvester-criterium

Hoe u een maximum of minimum van een functie kunt berekenen met de Hessische matrix

Voorbeeld van het berekenen van maxima en minima van een multivariabele functie

Het bepalen van de concaviteit of convexiteit van een functie met de Hessische matrix

Meer toepassingen van de Hessische matrix

Taylor-polynoom

Omrande jutematrix

Relatie met andere operaties

Relatie met de Jacobiaanse matrix

Laplace-operator

Laat een reactie achter Reactie annuleren